Інтеграл та його застосування
175.
1) F(x) = 9×2 – 2х +1?
F(x) – первісна для функції у = f(x) на заданому проміжку, якщо для всіх x з цього проміжку виконується співвідношення F'(x) = f(x).
Дійсно, F'(x) = 18х – 2 = 2(9х – 1) = f(x), -∞ < х < +∞, що й треба було довести.
2) 
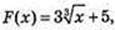Аналогічно. 
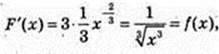0 < х < +∞.
3) 
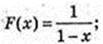
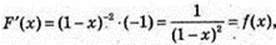1< x < +∞
4) F(x) = х × ех; F'(x) = 1 × ех + х × ех = ех(1 + х) = f(x), -∞< x < +∞·
5) 
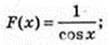
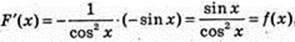
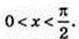
176.
1)
2) аналогічно, у = х7;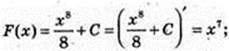 
3) y = x-3;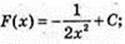 
4) 
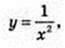
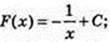
5) 
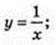F(x) = In |х| + С;
6) 
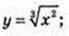
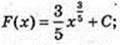
7) 
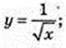
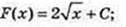
8) 
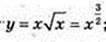
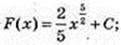
9) y = 3x;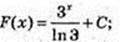 
10) у = 3-x;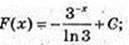 
11) у = еx; F(x) = еx + С.
177.
За даним графіком функціональна залежність є F(x) = -2x + 2.
Вся множина первісних F(x) = -2х + С.
178.
1) g(x) = x + с|x=1 = 1 → С = 0; g(x) = x
2)
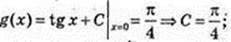
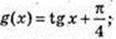
3) 
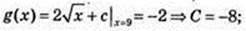
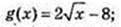
4) 
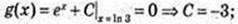G(x) = еx – 3;·
5) 
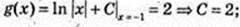g(x) = In |x| + 2.
Відповідь: 1) x; 2)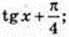 
3) 
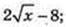4) ех -3; 5) In |x| + 2.
179.
1) 
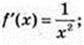
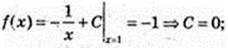
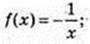
2) 
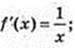
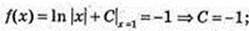f(x) = In |x| – 1.
180.
1) v(t) = t2 = x(t);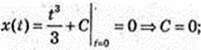 
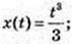
2) аналогічно,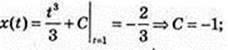 
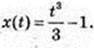
181.
V(t) = sin t = x'(t);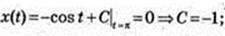 
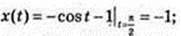
182.
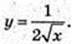Первісні: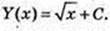 
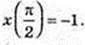
Для першої первісної х = 4, у = 1:
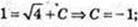
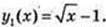
Для другої первісної x = 1,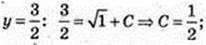
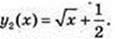
Графік другої первісної розташований вище графіка першої первісної.
Графік першої первісної можна одержати із графіка другої паралельним перенесенням на 1,5 одиниці у від’ємному напрямі вздовж осі Oy.
183.
1) 
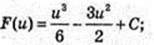
2) 
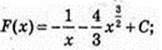
3) 
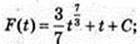
4) 
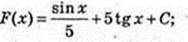
5) 
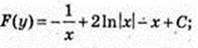
6) 
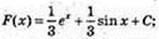
7) F(x) = x4- 2×2 + С;
8) 
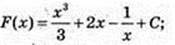
9) F(x) = -4 sin x – 5 cos x + 0,3x + С;
10)
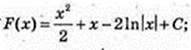
11)
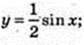
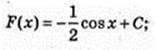
12) y = 3x + 1;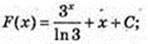 
13) 
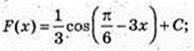
14) 
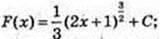
15) 
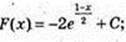
16) 
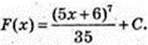
184.
1) 
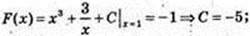
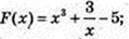
2) 
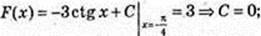F(x) = -3 ctg x;
3) 
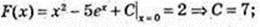F(x) = x2 – 5ex + 7;
4) 
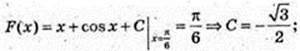
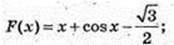
5) 
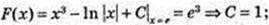F(x) = x3-In |x| + 1;
6) F(x) = ex + sin x,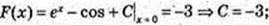 
F(x) = ex – cosx – 3;
7) f(x) = cos x;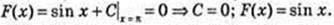 
185.
1) 
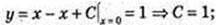y = 1.
2 )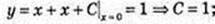 
y = 2x + 1.
186.
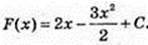F’ = 2 – 3x = 0; 
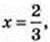F найм. на [0; 1].
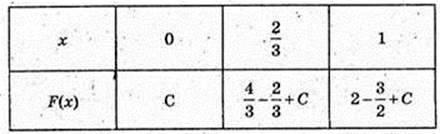
Fнайм. = C = 5 (з умови задачі), тому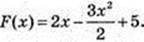 
187.
1) v(t) = x'(t) = t2 – 3t + 2;
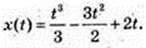
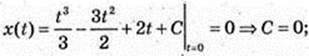
2) 
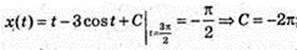x(t) = t – 3 cos t – 2π;
3) 
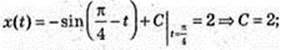
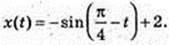
188.
1) Із малюнка 133
A) v(t) = kt + 6; t = 0, v = 30 → B = 30;
T = 5. v = 0 → 0 = 5k + 30 → k = -6 i v(t) = -6t + 30 = x'(t);
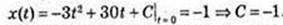x(t) = -3t2 + 30t – 1.
2) Із малюнка 133
Б) t = 0, v = 20 → b = 20;
T = 4,v = 40 →40 = 4tk + 20, k = 5 i v(t) = 5t + 20 = x'(t);
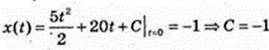I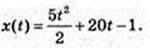 
189.
1) 
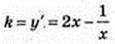(з умови), тоді у = x2 – In |x| + Clx=1 = 5 → C = 4;
Y = x2- ln |x| + 4;
2) 
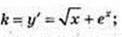
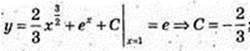
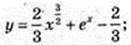
3) 
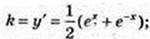
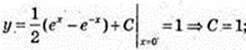
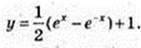
190.
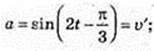
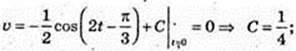
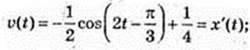
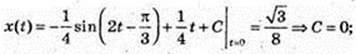
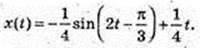
191.
1) Приріст функції Δf = f(x0 + Δх) – f(x0) = (1 + 2)3 + 1 – (12 + 1) = 8; Δf= 8.
2) 
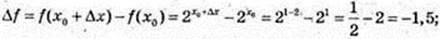Δf = -1,5.
192.
F(X) = sin x + С.
1) 
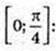
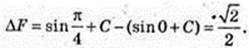
2) 
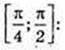
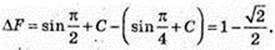
3) 
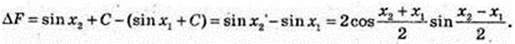
Прирости однакові.
193.
V(t) = 2t + 1 (з умови). Прискорення a = v’. a = 2 м/с2.
194.
Рисунки.
1)
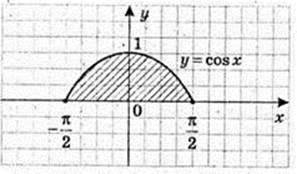
2)
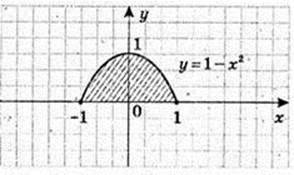
3)
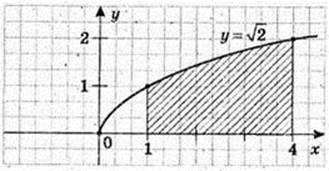
195.
1) 
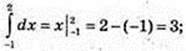
2) 
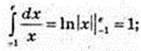
3) 
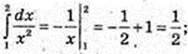
4) 
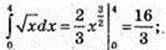
5)
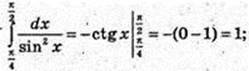
6) 
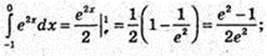
7) 
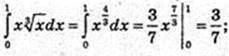
8) 
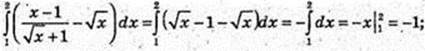
196.
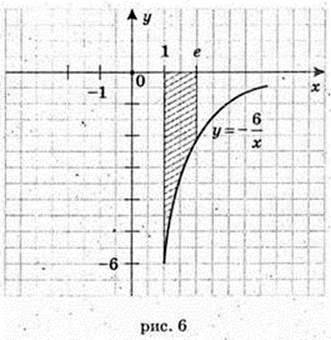
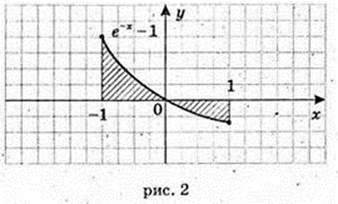
1) 
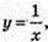x = 1, x = е, у = 0,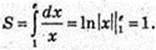 
2) у = 2x, у = 0, х = -1, x = 1. 
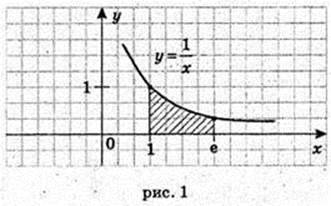
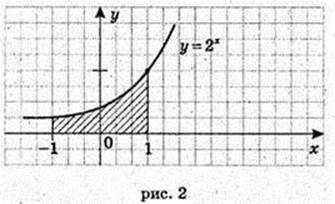
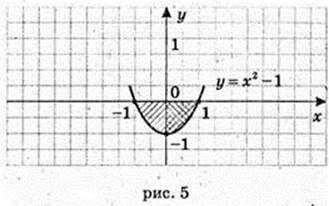
3) у = x2, x = -1, x = 2, у = 0.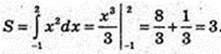 
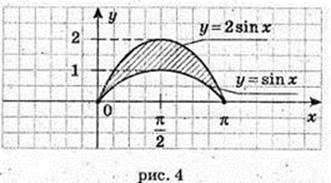
4) у = sin х, у = 0, x = 0, x = π.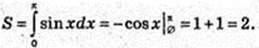 
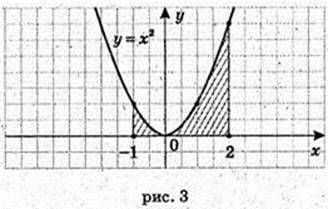
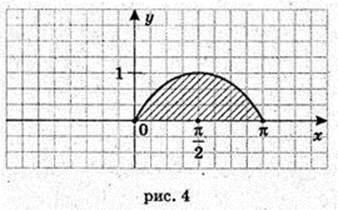
197.
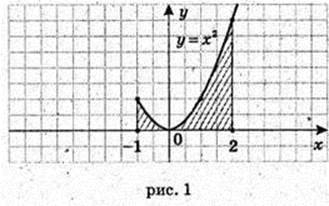
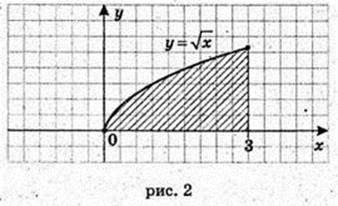
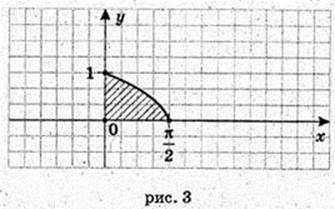
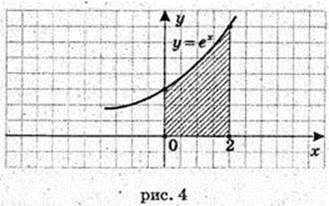
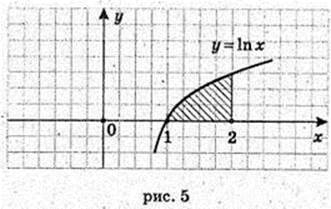
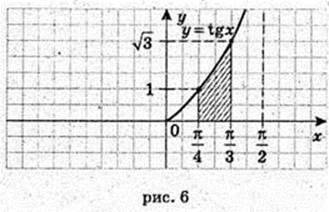
198.
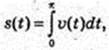в даному випадку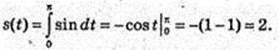
Відповідь: s = 2 м.
199.
Із графіка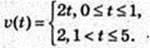 
1) 
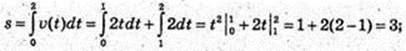
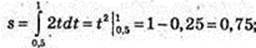
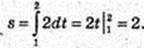
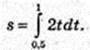
Відповідь: 1) 3 м; 0,75 м; 2 м; 2)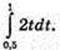 
200.
1) 
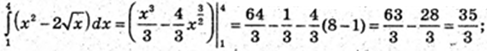
2) 
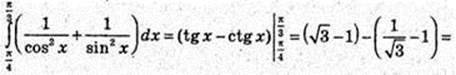
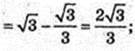
3) 
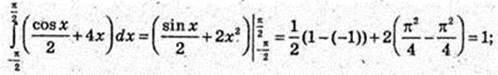
4) 
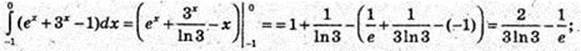
5) 
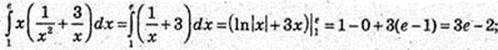
6) 
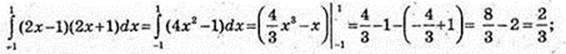
7) 
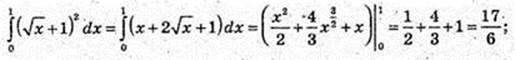
8) 
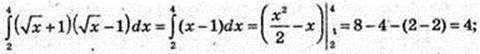
9) 
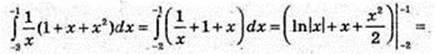
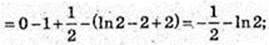
10)
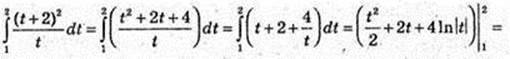
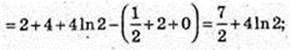
11) 
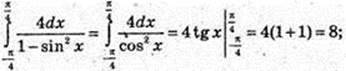
12) 
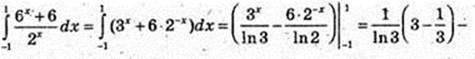
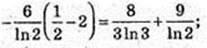
13) 
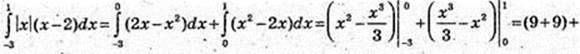
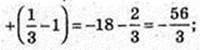
14) 
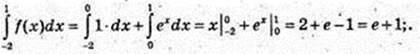
15) 
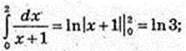
16) 
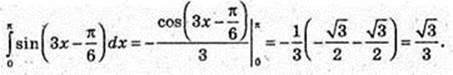
201.
1) 
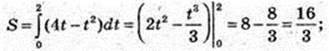
2) 
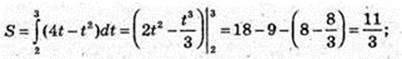
3) v(t) = 4t – t2 = 0,t(4 – t) = 0, t1 = 0, t2 = 4,
Тому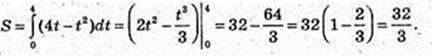 
202. v = 20 – 4t = 0 → t = 5, тому
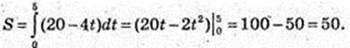
203.
1) 
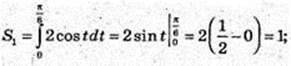
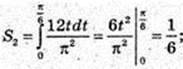
2) v1 = 2 cos t = 0,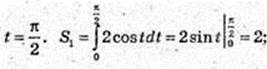 
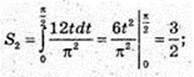
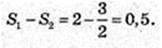
204.
1) 
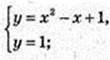x2 – x + 1 = 1; х2 – x = 0; х(х – 1) = 0;
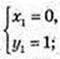
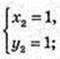A(0; 1), B(1; 1);
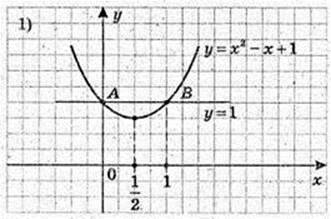
2) 
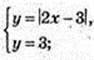|2х – 3| = 3; 2х -3 = ± 3;
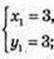
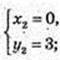A(0; 3), B(3; 3);
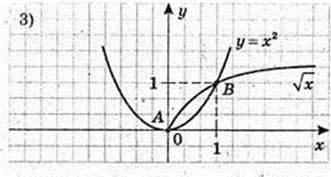
3) 
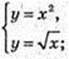
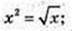
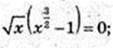
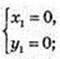
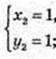A(0; 0), B(1; 1);
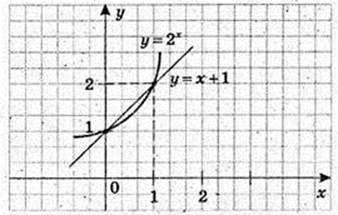
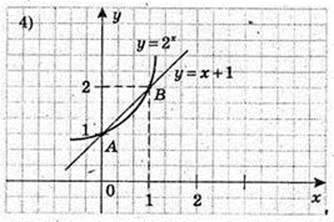
4) 
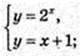2х = х + 1.
Графічно знайдемо корені: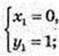 
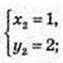
A(0; 1), B(1; 2).
205.
1) 
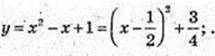у = |2х – 3|.
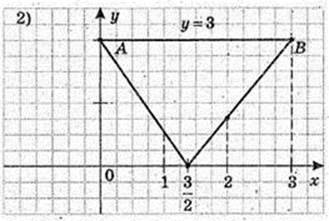
2)
206.
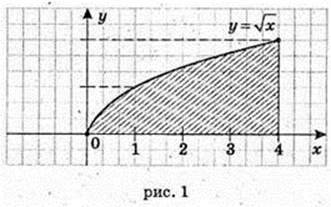
1) 
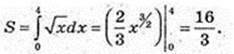
2)
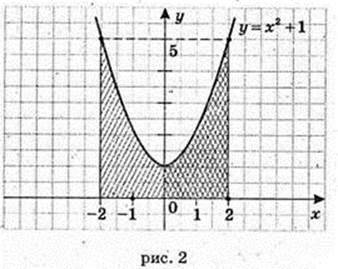
Використовуючи симетрію фігури
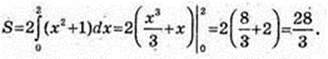
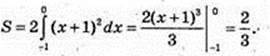
3)
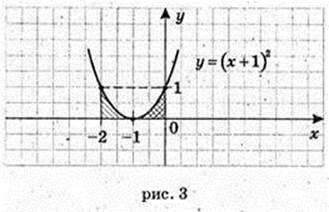
Згідно з симетрією фігури
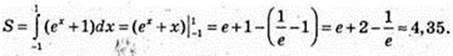
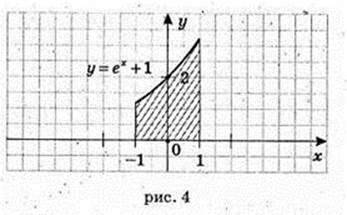
4)
5)
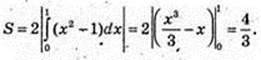
6)
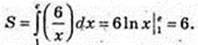
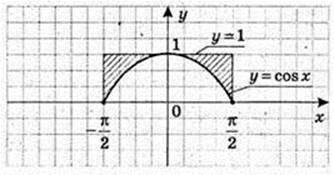
7) 
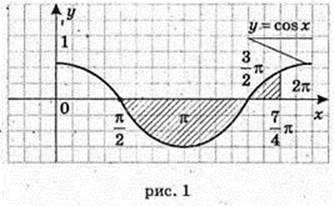
207.
1)
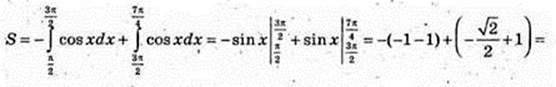
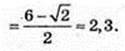
2)
3)
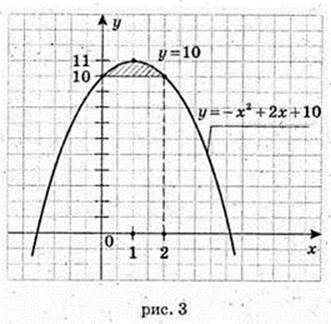
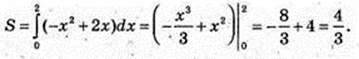
4) 
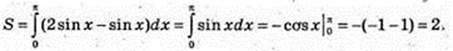
5)
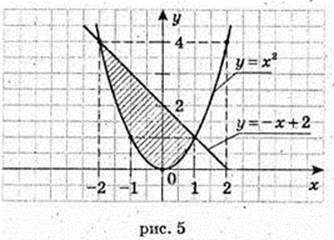
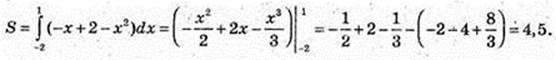
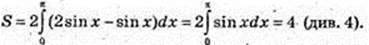
6)
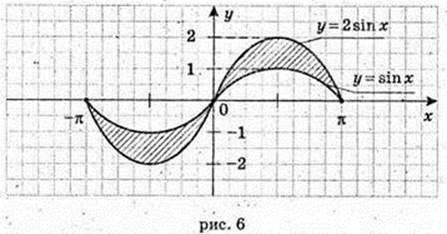
Враховуючи симетрію фігури
7)
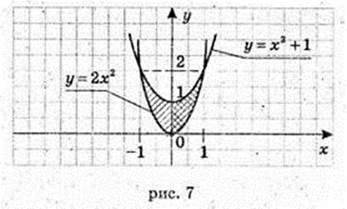
Враховуючи симетрію
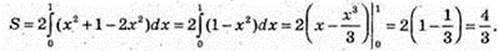
8)
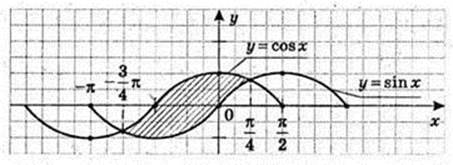
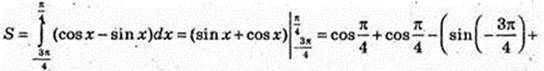
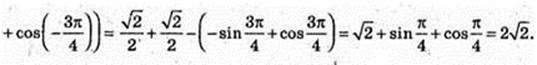
9) 
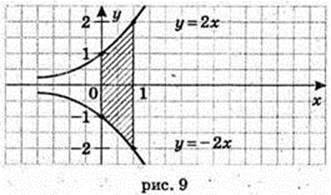
Згідно симетрії фігури
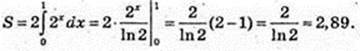
10)
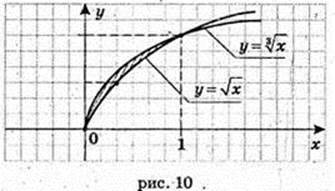
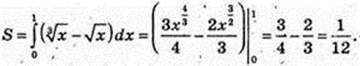
11)
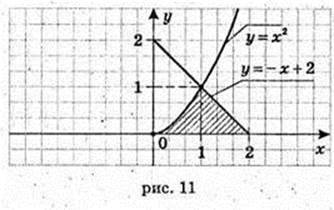
1 спосіб:
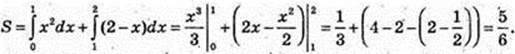
2 спосіб:
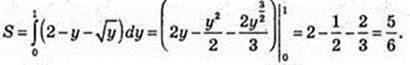
12)
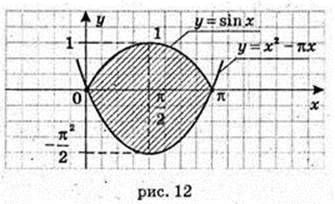
Згідно симетрії фігури
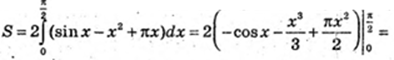
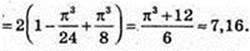
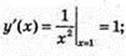
208.
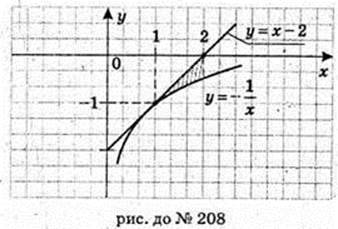
Рівняння дотичної у = у0 = у'(х0)(х – х0); x0 = 1, y0 = -1.
Y +1 = х – 1, у = х – 2.
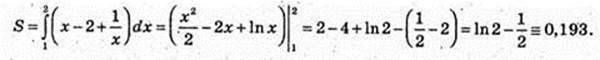
209.
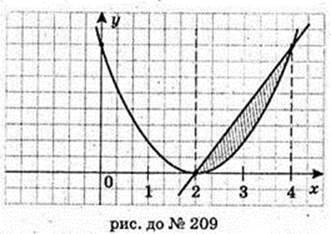
Первісна F(x) для функції f(x) = 2х – 4; F(x) = (2х – 4)dx = x2 – 4х + С.
Графік F(x) проходить через т. А(0; 4), тому C = 4. F(х) = x2 – 4x + 4 = (х – 2)2.
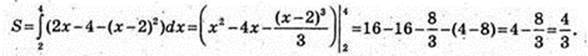
210.
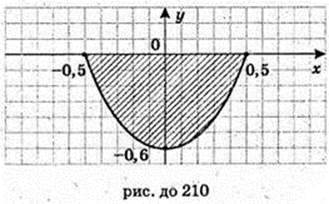
Рівняння параболи: y = ax2 + bx + T; x1 = -0,5; x2 = 0,5;
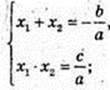
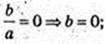
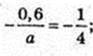
А = 2,4. x = 0, у = 0, y =-0,6; у=2,4 х2 – 0,6.
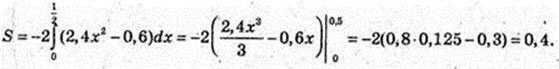
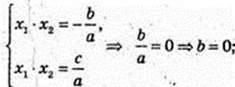
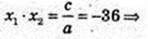
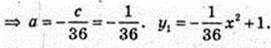
Друга парабола: х = 0, у = с = 2, b = 0,
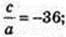
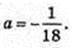
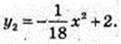
Площа
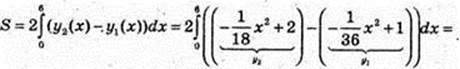
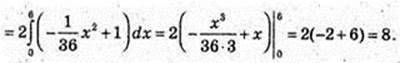
211.
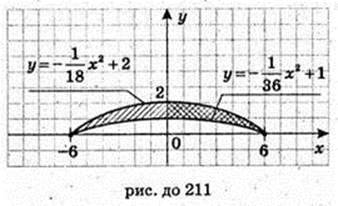
Знайдемо рівняння параболи. у = ах2 + bх + Т.
Х = 0,у = Т= 1. Корені x1 = -6, x2 = 6.
Маса опори за приведеною формулою:
M = р × S × d = 7,8 × 103 × 8 × 0,01 = 624.
212.
1) 
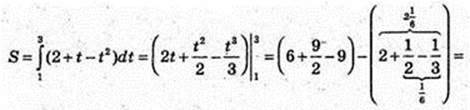
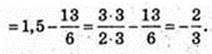
2) 
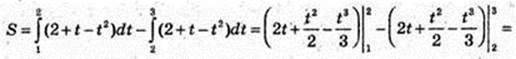
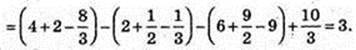
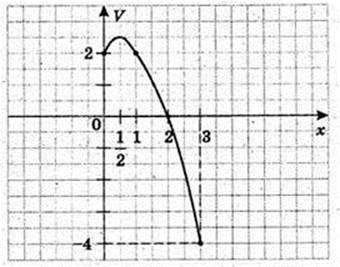
Пояснення: швидкість руху змінюється за законом
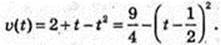
Графік приведено на малюнку, з якого видно, що на інтервалі [1; 2]
Швидкість додатна, а на інтервалі [2; 3] – від’ємна
І тіло рухається в протилежному напрямі, а пройдені шляхи складаються.
213.
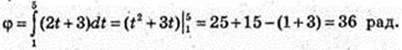
214.
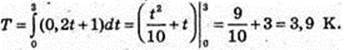
215.
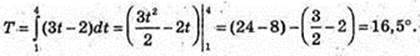
216.
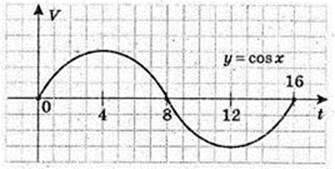
Швидкість гармонічного коливання змінюється за законом
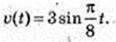
Графік приведено на малюнку.
1) Неважко помітити, що на проміжку |0; 8] швидкість додатна і точка рухається в одному напрямі, а на проміжку [8; 16] швидкість від’ємна і в момент t = 16 с точка повернеться в початкове положення, тобто переміщення дорівнює нулю.
2) 
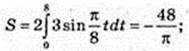
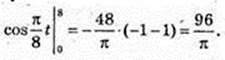
217.
Згідно із законом Гука F = kx. Для знаходження коефіцієнта k скористаємось
Умовою задачі, тобто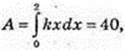 
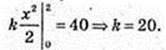
Робота для розтягування пружини на 3 см дорівнює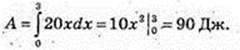
218.
1) 
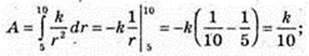
2) 
(1 votes, average: 5.00 out of 5)
Loading...