Коло і його елементи
Розділ 4. Коло і круг. Геометричні побудови
§ 21. Коло і його елементи
578. PL – хорда, що проходить через центр кола, називається діаметром.
579. 1) 5 х 2 = 10(см);
2) 4,7 х 2 = 9,4 (дм).
580. 1) 8 мм х 2 = 16 мм;
2) 4,8 см х 2 = 7,6 см.
581. 1) 6 дм : 2 = 3 дм;
2) 2,4 см : 2 = 1,2 см.
582. 1) 20 см : 2 = 10 см;
2) 5,6 дм : 2 = 2,8 дм.
583.
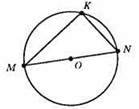
OМ = 4 см. ∠NKM = 90°.
584.
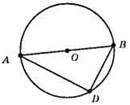
OМ = 3,6 см. ∠BDA = 90°.
585.
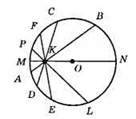
Через точку К, взяту всередині кола, можна провести тільки один діаметр i безліч хорд.
586.
Через т. А, взяту на колі, можна провести тільки один діаметр і безліч хорд.
587. Оскільки радіус кола дорівнює 5 см, то діаметр дорівнює 10 см. Діаметр кола є найбільшою хордою, отже, хорда цього кола менша або дорівнює 10 см.
1) Може; 2) може; 3) може; 4) може; 5) не може.
588. Хорда кола не більша від діаметра, тобто хорда менша або дорівнює 8 дм.
1) Може; 2) може; 3) може; 4) може; 5) не може,
589. ?AOD = ?ВОС за двома сторонами і кутом між ними, оскільки АО = ВО – як радіуси кола, OD = ОС – як радіуси кола, ∠AOD = ∠СОВ – як вертикальні кути.
590. ?MON = ?РОК за двома сторонами і кутом між ними,
591. ?ОАВ – рівнобедрений, оскільки ОА = OB – як радіуси кола, тоді ∠А = ∠В.
1) Якщо ∠A = 52°, то ∠B = 52°, ∠O = 180° – ∠А – ∠B = 180° – 52° – 52° = 76°.
2) Якщо ∠О = 94° то ∠B = (180° – АО) : 2 = (180° – 94°) : 2 = 43°.
Відповідь: 1) 76°; 2) 43°.
592. ?АОВ – рівнобедрений, оскільки ОА = OB – як радіуси кола, тоді ∠А = ∠B.
1) Якщо ∠B = 48°, то ∠А = 48°, ∠О = 180° – ∠A – ∠B = 180° – 48° – 48° = 84°.
2) Якщо ∠О = 102°, то ∠А – (180° – ∠O) : 2 = (180° – 102°) : 2 = 39°.
Відповідь: 1) 84°; 2) 39°.
593. ?СОВ – рівнобедрений, оскільки ОС = ОB – як радіуси кола, тоді ∠С = ∠B. ∠СОВ + ∠СОА = 180° – як суміжні кути. Звідси ∠СОВ = 180° – ∠COA = 180° – 32° = 148°. Отже, ∠СВА = (180° -∠СОВ) : 2 = (180° – 148°) : 2 = 16°.
Відповідь: 16°.
594. ?СОВ – рівнобедрений, оскільки ОС = OB – як радіуси кола, тоді ∠С = ∠B. ∠СОВ = 180° – (∠С – ∠B) = 180° – 18° – 18° = 144°. ∠СОВ + ∠СОА = 180° – як суміжні кути. Звідси ∠СОА = 180° – ∠СОВ = 180° – 144° = 36°.
Відповідь: 36°.
595.
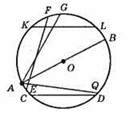
1) ОА = OB = 5 см. Хорд довжиною 6 см можна провести безліч, наприклад CD, EF, KL.
2) Точка А належить колу. З даної точки можна провести дві хорди завдовжки 6 см – AG i AQ.
596.
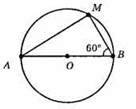
?АМВ – прямокутний (згідно з теоремою 2 про кут, під яким видно діаметр з точки кола), ∠M = 90°. ∠MAB = 90° – 60° = 30°. AB = 2MB = 2 х 5 см = 10 см.
Відповідь: 10 см.
597.
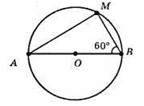
?AMB – прямокутний (згідно з теоремою 2 про кут, під яким видно діаметр з точки кола), ∠M = 90°. ∠A 90° – ∠B = 90° – 60° = 30°. MB = 1/2AB = 1/2 • 18 = 9 см.
Відповідь: 9 см.
598.
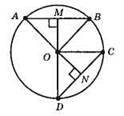
Нехай AB і CD – хорди. ОМ ⊥ AB, ON ⊥ LCD і ОМ = ON. Доведемо, що AB = CD.
Оскільки ОМ ⊥ AB, ON ⊥ CD, то AM = MB, CN = CD, тобто, щоб довести, що AB = CD, досить довести, що AM = CN. ?АОМ = ?CON (за гіпотенузою і катетом: ОМ = ON – за умовою, ОА = ОС – як радіуси кола), тоді AM = CN. Отже, AB = 2АМ = 2CN = CD.
599.
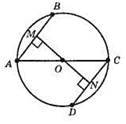
Нехай AB = CD, ОМ ⊥ AB, ON ⊥ CD. Доведемо, що ОМ = ON.
Оскільки ОМ ⊥ AB, то AM = MB, оскільки ON ⊥ CD, то CN = ND.
?OMA = ?ONC (за гіпотенузою і катетом: ОА = ОС – як радіуси, AM = CN – як половини рівних відрізків). Тоді ОМ = ON.
600.
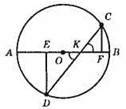
Нехай CF ⊥ AB, DE ⊥ AB. ∠CKF = ∠EKD = 30°. CK = 4 см, MD = 7 см.
3 ?KCF: ∠F = 90°, CF = 1/2KC (оскільки ∠CKF = 30°), CF = 1/2 • 4 = 2 CM.
3 ?DEK: ∠E = 90°, ED = 1/2KD (оскільки ∠EKD = 30°), ED = 1/2 • 7 = 3,5 CM.
Відповідь: 2 см, 3,5 см.
601.
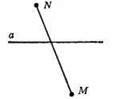
602.
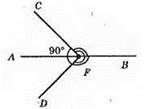
Нехай ∠CFB = ∠DFВ, ∠CFD = 90°. Оскільки ∠CFB = ∠DFB, то ∠CFA = ∠DFА – як суміжні кути до рівних кутів. Оскільки ∠CFD = 90°, то ∠CFA = ∠DFA = 90° : 2 = 45°, тоді ∠CFB = ∠DFB = 180° – 145° = 35°.
Відповідь: 35°.
603.
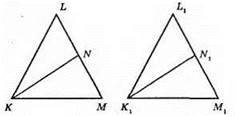
Нехай у рівнобедрених трикутників KLM і K1L1M1 KL = LM, K1L1 = L1M1, KM = K1M1, KN ⊥ LM, K1N1 ⊥ L1M1, KM = K1M1. Доведемо, що? KLM = ?K1L1M1. ?KNM = ?K1N1M1 (за гіпотенузою і катетом:KM = K1M1, KN = K1N1 – за умовою). З рівності трикутників маємо ∠M = ∠M1, ∠K = ∠M, ∠K1 = ∠M1 – оскільки? KLM і? K1L1M1 – рівнобедрені. ?KLM = ?K1L1M1 за стороною і двома прилеглими кутами (КМ = K1M1 – за умовою, ∠K = ∠K1, ∠M = ∠M1 – за доведенням).
604.
З’їла Марійка.
У коробці залишилося 16 цукерок.