КОЛО І КРУГ. КРУГОВИН СЕКТОР
Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ
§ 16. КОЛО І КРУГ. КРУГОВИН СЕКТОР
З усіх замкнених кривих ліній на площині найдосконалішою вважають коло. Якщо закріпити один кінець відрізка в якійсь точці, а потім повертати відрізок, то інший його кінець буде рухатися саме по колу. Тому кола зображують за допомогою циркуля (мал. 25).
Мал. 25
Запам’ятайте!
Коло – це фігура, усі точки якої знаходяться на площині на однаковій відстані від однієї точки, що називається центром кола.
На малюнку 26 ви бачите коло з
Якщо будь-яку точку кола і його центр О сполучити відрізком, то дістанемо радіус кола. На малюнку 26 відрізки ОА і ОВ – це радіуси кола із центром у точці О. Отже, ОА = ОВ.
Радіус позначають буквою R. Записують: ОА = R.
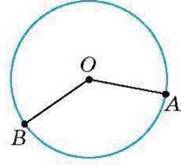
Мал. 26
Зверніть увагу:
Усі радіуси кола дорівнюють один одному.
Проведемо радіуси ОА і ОВ кола так, щоб вони лежали на одній прямій (мал. 27). Отримали відрізок АВ, який називають діаметром кола.
Діаметр АВ кола вдвічі довший за радіус ОА, а радіус ОА є половиною діаметра АВ. Отже:
АВ = 2 ∙ О А.
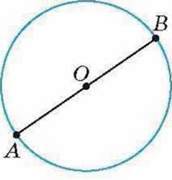
Мал. 27
Запам’ятайте!
Формула
Діаметр кола дорівнює подвоєному радіусу: D = 2%.
Задача 1. З найдіть радіус кола з діаметром 8 см.
Розв’язання. Діаметр кола – удвічі довший за радіус. : Отже, R = D : 2 = 8 : 2 = 4 (см).
? Чи можна знайти довжину кола? Так.
Адже коло – це лінія. Але лінійкою коло не виміряти. Проведемо дослід. Візьмемо склянку, поставимо її на аркуш паперу та обведемо олівцем (мал. 28). Отримали коло.
Якщо обв’язати склянку ниткою, а потім розпрямити її, то довжина нитки буде дорівнювати довжині зображеного кола.
Довжину кола позначають буквою С.
Провівши кілька таких вимірювань, помітимо закономірність: що більшим є діаметр кола то більшою є його довжина. Тобто довжина кола прямо пропорційна довжині діаметра.
Відношення довжини кола до довжини його діаметра дорівнює тому самому числу для всіх кіл. Це число позначають грецькою буквою п.
Число п читають: “пі”.
Число п – нескінченний десятковий дріб. п= 3,14159265358979… Тому при обчисленнях його округлюють: п ≈ 5,14.
Mал. 28
Діаметр позначають буквою D Записують: АВ = D.
Запам’ятайте!
Формула довжини кола
Довжина кола дорівнює подвоєному добутку числа п і радіуса:
С=2пR.
Задача 2. Знайдіть довжину кола з діаметром 10 см.
Розв’язання.
Спосіб 1. Діаметр кола – удвічі довший за радіус. Отже,
R = D :2 = 10:2 = 5 (см).
С = 2пR, = 2 ∙ 3,14 -5 = 31,4 (см).
Спосіб 2. Оскільки D = 2R, то C=2пR=п(2R) = пD.
Тому С = 3.14 ∙ 10 = 31,4 (см).
Зверніть увагу:
Оскільки D= 2R, то С = пD.
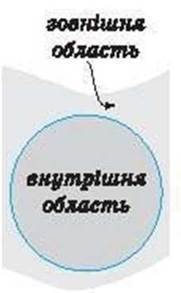
Мал. 29
Коло поділяє площину на дві частини – внутрішню і зовнішню (мал. 29). Про внутрішню частину кажуть, що коло обмежує цю частину площини. Коло разом із частиною площини, яку воно обмежує, утворює відому вам фігуру – круг (мал. 30). Центр кола вважають і центром круга, радіус і діаметр кола – радіусом і діаметром круга. На відміну від кола, центр круга є точкою круга.
Мал. З0
Запам’ятайте!
Формула площі круга
Площа круга дорівнює добутку числа х і квадрата радіуса:
S = пR.
Задача 3. Знайдіть площу круга, діаметр якого дорівнює 8 см.
Розв’язання. Діаметр кола – удвічі довший за радіус.
Тому R=D:2 = 8 :2=4 (см). Звідси:
S = пR2 =
= 3,14 ∙ 42 = 3,14 ∙ 16 = 50,24 (см2).
Отже, площа даного круга становить 50,24 см2.
Якщо в круїзі провести два радіуси ОА й ОВ, то круг буде поділено на дві частини (мал. Зі), які називаютв секторами.
На малюнку 32 показано сектор СО D з кутом 60°.
Діаметр CD круга поділяє круг на два рівні сектори (мал. 33). Такі сектори є половинами круга. Кут кожного з таких секторів дорівнює 180°. Якщо кожну половину круга поділити навпіл, отримаємо 4 рівні сектори (мал. 34).
Кут кожного з них дорівнює 90°.
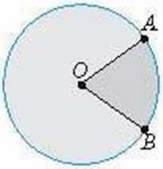
Maл. 31
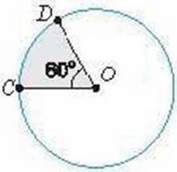
Мал. 32
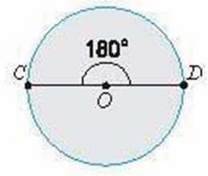
Мал. 33
Мал. 34
Зверніть увагу:
– у рівних секторів – рівні кути;
– сума кутів усіх секторів, на які поділено круг, дорівнює 360°.
Задача 4. Круг поділено на 3 рівні сектори. Знайдіть кут сектора.
Розв’язання. Сума кутів усіх даних секторів дорівнює 360°. Круг поділено на 3 рівні сектори, тому 360° : 3 = 120°. Отже, кут сектора дорівнює 120°.
Задача 5. Круг поділено на 3 сектори з кутами 80°, 120° і 163°. Яку частину круга становить кожен сектор? Розв’язання. Кожен із даних секторів становить таку частину круга, яку його кут становить від 360°. Звідси: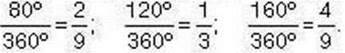 
Дізнайтеся більше
1. Найперші відомі записи наближень числа п датують близько 1900 р. до н. е.:
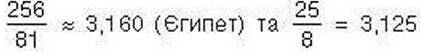
(Вавилон). Вважають, що Архімед (287-212 pp. до н. е.) першим запропонував математичний спосіб обчислення числа п. Про суть цього способу ви дізнаєтесь у курсі геометрії.
Вільям Джоне
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Яку фігуру називають колом?
2. Що таке радіус кола? Діаметр кола?
3. Що показує число п?
4. Чому дорівнює довжина кола?
5. Яку фігуру називають кругом?
6. Чому дорівнює площа круга?
7. Поясніть, як можна отримати сектор круга.
8. Чому дорівнює сума кутів усіх секторів, на які поділено круг?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
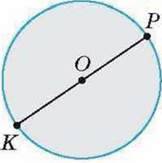
679′. За малюнком 35 назвіть:
1) центр кола;
2) радіус кола;
3) діаметр кола.
680′. Чому дорівнює значення відношення довжини кола до довжини його діаметра?
681. Чи правильно, що коло більшого діаметра має більшу довжину? Відповідь поясніть.
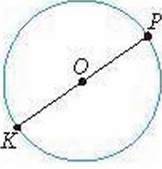
Мал. 35
682′. За малюнком 36 назвіть:
1) центр круга;
2) радіус круга;
3) діаметр круга.
683 . На скільки секторів можна поділити круг?
684′. Чи правильно, що сума кутів усіх секторів, на які поділено круг, дорівнює:
1)90°; 2) 180°; 3)360°?
685°. Радіус кола – R, діаметр кола – D, довжина кола – С. Якими даними треба доповнити таблицю З?
Таблиця З
Мал. 36
686°. Як зміниться довжина кола, якщо: 1) його радіус збільшити у 2 рази; 2) його діаметр зменшити в 4 рази?
687°. Як зміниться радіус кола, якщо довжину кола: 1) збільшити в 3 рази; 2) зменшити у 2 рази?
688°. Радіус кола – R, діаметр кола – D, довжина кола – С, площа круга – S. Якими даними треба доповнити таблицю 4?
Таблиця 4
689°. Як зміниться площа круга, якщо: 1) його радіус збільшити в 3 рази; 2) його діаметр зменшити в 4 рази?
690°. Як зміниться радіус круга, якщо його площу:
1) збільшити в 4 рази; 2) зменшити в 9 разів?
691°. На скільки секторів поділяють коло 2 діаметри?
692°. Знайдіть кут сектора, якщо круг поділено:
1) на 5 рівних секторів; 2) на 6 рівних секторів.
693°. Круг поділено на 10 рівних секторів. Знайдіть кут сектора.
694. Знайдіть площу круга, довжина кола якого дорівнює:
1)37,68см; 2)31,4дм.
695, Яка площа круга, якщо довжина кола дорівнює 8п см?
696. Обчисліть довжину кола, якщо площа круга дорівнює:
1) 28,26 см2; 2) 78,5 дм2.
697. Яка довжина кола, якщо площа круга дорівнює 50,24 см2?
698. Як зміниться площа круга, якщо довжину кола, що його обмежує: 1) збільшити у 2 рази; 2) зменшити в 3 рази?
699. Як зміниться довжина кола, що обмежує круг, якщо площу круга: 1) збільшити в 4 рази; 2) зменшити в 9 разів?
700. Діаметр круглого диска дорівнює 12 см. Знайдіть довжину кола, що обмежує цей диск, і площу цього диска.
701. Колесо на відстані 240 м зробило 400 обертів. Знайдіть діаметр колеса (п ≈ 3).
702. Діаметр колеса дорівнює 80 см. Скільки повних обертів зробить колесо, якщо автомобіль проще 150 км (п ∙ 3)?
703. Круг поділено на сектори. Знайдіть кути цих секторів, якщо вони відносяться, як:
1) 2 : 3 : 4; 2) 2 : 4 : 5 : 7.
704. Знайдіть кути секторів круга, якщо вони відносяться, як 3 : 4: 5.
705. Чи можна стверджувати, що рівні сектори мають рівні площі?
706*. Чи існує круг, у якого площа виражається таким самим числом, що й довжина кола, яке обмежує цей круг (найменування величин не враховувати)?
707*. Чи можна вирізати з квадрата зі стороною 2 дм круг, довжина кола якого дорівнює 9,42 дм?
708*. Обчисліть площу зафарбованих фігур на малюнках 37-38.
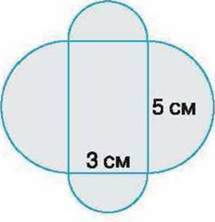
Мал. 37
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
709. Із аркуша паперу вирізано круг. Як, перегинаючи аркуш, знайти центр цього круга?
710. Яка клумба для квітів має більшу площу: та, що має форму квадрата зі стороною 4 м, чи та, що має форму круга з діаметром 4 м?
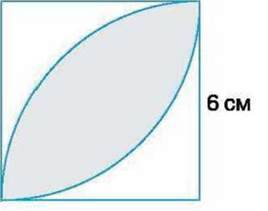
Мал. 38
ЗАДАЧІ НА ПОВТОРЕННЯ
711. Обчисліть зручним способом:
1) (3,83 ∙ (38,75-33,55)+ (47,79-42,59) ∙ 1,17) ∙ 11;
2) 2,5 ∙1,725 ∙1,25 ∙ 0,8 -4+ 12,75.
712. Із трьох яблунь зібрали 100 кг яблук. З першої яблуні зібрали 56 кг яблук, а з другої –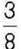 
маси яблук, що зібрали з першої
Яблуні. Скільки кілограмів яблук зібрали з третьої яблуні?
(1 votes, average: 5.00 out of 5)
Loading...