Головна ⇒ 📌Довідник з геометрії ⇒ Конус, вписаний у кулю
Конус, вписаний у кулю
Геометрія
Комбінації геометричних тіл
Конус, вписаний у кулю
Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа).
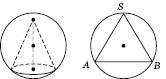
Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус кулі дорівнює радіусу кола, описаного навколо осьового перерізу конуса.
Related posts:
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
- Конус Геометрія Тіла обертання Конус Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса. Конус називається Прямим (далі просто “конус”), якщо […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Зрізаний конус Геометрія Тіла обертання Зрізаний конус Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса. Така площина відтинає від конуса менший конус. Частина, що залишилась, називається Зрізаним конусом (див. рисунок): ; Зверніть увагу на осьовий переріз зрізаного конуса. Це рівнобічна трапеція, в якої основи – […]...
- Конус і зрізаний конус 983. Нехай дано конус, твірна якого AM = l, і нахилена до площини основи під кутом ∠MAO = α. А) ΔAMO – прямокутний. OM – висота, OM = l × sin α; Б) AO – радіус основи конуса. AO = l × cos α; В) ΔAMB – осьовий переріз; Г) площа основи конуса – площа […]...
- ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...
- Описані кулі Геометрія Комбінації геометричних тіл Описані кулі Кожна грань вписаного у сферу многогранника є вписаним у деяке коло многокутником. Основи перпендикулярів, які опущені з центра описаної кулі на площини граней, є центрами описаних навколо граней кіл. Отже, центром кулі, описаної навколо многогранника, є точка перетину перпендикулярів до площини граней, які проведені через центри кіл, описаних навколо […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Наслідки з теореми про вписаний кут. Розв’язування задач Урок № 21 Тема. Наслідки з теореми про вписаний кут. Розв’язування задач Мета: домогтися засвоєння учнями змісту наслідків із теореми про вписаний кут та способів їх доведення. Сформувати вміння: – відтворювати зміст вивчених тверджень; – знаходити на рисунку об’єкти, властивість яких описується цими наслідками; – використовувати вивчені твердження під час розв’язування задач на обчислення кутів […]...
- Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Кути у колі – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Кути у колі Центральний кут – кут з вершиною у центрі кола. Вписаний кут – кут, вершина якого лежить на колі, а сторони перетинають це коло. Вписаний у коло кут дорівнює половині відповідного йому центрального кута або доповнює половину цього кута до 180° ....
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Градусна міра дуги. Вписаний кут Урок № 20 Тема. Градусна міра дуги. Вписаний кут Мета: домогтися засвоєння учнями змісту понять: плоский кут (у неявному вигляді), центральний кут, дуга кола, що відповідає даному центральному куту, градусна міра дуги кола, вписаний кут, – а також засвоєння учнями змісту властивості вписаного кута (про вимірювання вписаного кута). Формувати вміння: – відтворювати зміст вивчених тверджень; […]...
- Вписаний та описаний чотирикутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Вписаний та описаний чотирикутники Якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло: A + C = 180°, B + D = 180°. Якщо суми протилежних сторін чотирикутника рівні, то в нього можна вписати коло: AB + CD = BC + AD...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...
- Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...
- Конуси 1050. ΔSAPO: ∠АОР = 90°, ОЕ = АЕ = ЕР = 6,5 см → АР = 13 см. АО = 5 см. R = AO, L = АР = 13 см, r = 5 см. Sп. к. = πrl + πr2 = π(5 × 13 + 52) = 90π. S = 90π см2. 1051. ΟΑ […]...
- Вписана та описана сфера 1. Нехай О А – радіус кулі, ОА = 1 см. АВ = ΚΚ1 = 2ОА = 2 см. CD = 2СО = 2 см. Sбіч. = PKLMN× КК1 = 4 × 2 × 2 = 16 (см2). Відповідь: 16 см2. 2. Нехай АВ =AD = ВВ1 = а. З ΔABD: З ΔΒ1BD: В1D2 = […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...
- Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сторонами a, b і c. – формула периметра трикутника. Сума всіх кутів довільного трикутника дорівнює . Кожний трикутник має принаймні два гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...
- Вписаний чотирикутник – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Вписаний чотирикутник Усі вершини лежать на колі. Сума протилежних кутів дорівнює 180°....
- Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...
- КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...