Головна ⇒ 📌Довідник з математики ⇒ Координатна площина
Координатна площина
Математика – Алгебра
Раціональні числа
Координатна площина
Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку – точці О. Ці прямі називаються Осями координат. Горизонтальну пряму називають Віссю абсцис І позначають Ox, вертикальну – Віссю ординат І позначають Oy. Точку О називають Початком координат. Ці координатні прямі утворюють Декартову прямокутну систему координат. Площина, на якій задана прямокутна система координат, називається Координатною площиною. Через будь-яку точку
Нехай ці прямі перетнуть відповідно вісь абсцис – у точці з координатою а, а вісь ординат – у точці з координатою b.
Пара чисел (а, b) визначає положення точки А на координатній площині й називається її Координатами. Позначають А(а, b). Число а називається абсцисою точки А, число b – її ординатою. Зверніть увагу: має значення, в якому порядку записані числа а і b. Точка В(b; а) не збігається з А(а; b).
Якщо точка лежить на осі абсцис, то її ордината дорівнює 0; якщо точка лежить на осі ординат, то її абсциса дорівнює нулю. Початок координат
Осі координат розбивають площину на 4 частини, які називаються Координатними чвертями. Нумерація чвертей, знаки координат у кожній чверті, а також приклади точок з їх координатами показані на рисунку.

Таким чином, щоб побудувати, наприклад, точку М(k; р), треба поставити олівець в О(0; 0), потім пересунутися по осі абсцис на
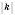 одиничних відрізків праворуч (якщо
одиничних відрізків праворуч (якщо 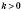 ) або ліворуч (якщо
) або ліворуч (якщо 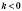 ). Від отриманої точки на осі абсцис треба рухатись угору на
). Від отриманої точки на осі абсцис треба рухатись угору на 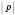 одиничних відрізків (якщо
одиничних відрізків (якщо 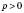 ) або униз (якщо
) або униз (якщо 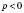 ).
).



 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- КООРДИНАТНА ПЛОЩИНА Розділ 5 ВИРАЗИ І РІВНЯННЯ § 34. КООРДИНАТНА ПЛОЩИНА Ви вже знаєте, що таке координатна пряма (мал. 162). На ній точка О – початок відліку, стрілка показує напрямок зростання чисел, а ціна поділки становить одну одиницю. Мал. 162 Проте на практиці часто доводиться користуватися орієнтирами не тільки вздовж прямої, а й на площині. Ви знаєте, […]...
- КООРДИНАТНА ПЛОЩИНА. ГРАФІК ФУНКЦІЇ РОЗДІЛ 4 ФУНКЦІЇ &16. КООРДИНАТНА ПЛОЩИНА. ГРАФІК ФУНКЦІЇ Із кypcу математики 5-6 класів ви знаєте, що таке шкала, координатна пряма і координатна площина. Пригадаємо основні відомості. Щоб увести прямокутну систему координат на площині, треба: провести дві координатні прямі з рівними одиничними відрізками так, щоб вони перетиналися під прямим кутом у початку їх відліку (початку координат); […]...
- Координатна площина. Графік функції 824. 1) абсциса точки А дорівнює -3; 2) ордината точки А дорівнює 7. 825. Точка А в II чверті; В в IV чверті; С в IV чверті; D в II чверті; Е в І чверті; F у III чверті; K у II чверті; L у III чверті. 826. 1) ні; 2) ні; 3) ні. 827. […]...
- Перпендикулярні та паралельні прямі. Координатна площина. Графіки залежностей Урок № 118 Тема. Перпендикулярні та паралельні прямі. Координатна площина. Графіки залежностей Мета: підготувати учнів до виконання до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Задачу № 2 перевіряємо фронтально, бо вона є нестандартною, за описом треба зробити графік (див. рис […]...
- Координатна площина Урок № 113 Тема. Координатна площина Мета: відпрацювати навички “читати” готові рисунки з точкам на координатній площині та будувати точки із заданими координатами; здійснити діагностику знань і вмінь з теми. Тип уроку: застосування знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Бажано звернути увагу на задачу 4 – повторити спосіб […]...
- Перпендикулярні та паралельні прямі. Координатна площина Урок № 119 Тема. Перпендикулярні та паралельні прямі. Координатна площина Мета: перевірити й оцінити рівень знань та вироблених умінь і навичок, які є обов’язковими для опанування теми. Тип уроку: контроль і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Збираємо зошити з домашньою контрольною роботою для перевірки. III. Умова […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Координатна площина. Графіки залежності Урок № 117 Тема. Координатна площина. Графіки залежності Мета: вдосконалити вміння учнів, вироблені в ході вивчення теми шляхом розв’язування задач підвищеної складності; відпрацьовувати обчислювальні навички. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Під час аналізу виконання задачі 1 звертаємо увагу на те, що для відповіді на […]...
- Прямокутна система координату просторі Урок 44 Тема. Прямокутна система координату просторі Мета уроку: знайомство з декартовою прямокутною системою координат у просторі. Обладнання: модель куба. Хід уроку І. Аналіз виконання тематичного оцінювання II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення й виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Прямокутна система координат на […]...
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- КООРДИНАТНА ПРЯМА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 22. КООРДИНАТНА ПРЯМА У п’ятому класі додатні числа і число 0 ви позначали на координатному промені (мал. 88). Продовжимо координатний промінь ОХ за його початок вліво. На добудованому промені нанесемо таку саму шкалу, як і на промені ОХ (мал. 89). Дістали координатну пряму. Точка О називається […]...
- Площина. Пряма. Промінь УРОК 11 Тема. Площина. Пряма. Промінь Мета: закріпити знання, здобуті на попередньому уроці, про властивості прямої, площини і променя; розвивати просторову уяву учнів; перевірити засвоєння матеріалу з тем “Відрізок” та “Площина. Пряма. Промінь” під час виконання самостійної роботи. Тип уроку: засвоєння навичок та вмінь. Хід уроку I. Перевірка домашнього завдання та актуалізація опорних знань Усні […]...
- Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...
- Площина. Пряма. Промінь Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 1. НАТУРАЛЬНІ ЧИСЛА 4. Площина. Пряма. Промінь Розміри вашого зошита не дають можливості будувати відрізки великої довжини. А уявіть собі, що аркуш зошита збільшився до розмірів стола, тенісного корту, навіть футбольного поля. Такий “аркуш” слугує прикладом частини площини. Площина нескінченна, тому її не можна зобразити. Цю […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Рівняння прямої Геометрія Декартові координати на площині Рівняння прямої Будь-яка пряма в декартових координатах x, y має рівняння виду: , де a, b, c – деякі числа. Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі “Алгебра. 8 клас” (“Лінійна функція”). Рівняння прямої, яка перетинає осі координат в точках і , […]...
- Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...
- Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Прямокутна система координат на площині УРОК № 22 Тема. Прямокутна система координат на площині Мета уроку: узагальнення та систематизація матеріалу про декартову прямокутну систему координат. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують прямокутну систему координат. Застосовують вивчені означення до розв’язування задач. Хід уроку I. Перевірка домашнього завдання […]...
- Геометричні фігури, точка, пряма, промінь Розділ 1. Елементарні геометричні фігури та їхні властивості § 1. Геометричні фігури, точка, пряма, промінь 1. 1) Прямій а належать точки А, В, С. 2) Прямій b належать точки Р i В. 3) Прямій а і прямій b належить точка В. 4) Точки А і С належать прямій а, але не належать прямій b. 5) […]...
- ГРАФІКИ Соціологія короткий енциклопедичний словник ГРАФІКИ – засоби наочного подання соціол. інформації, які забезпечують наочність та полегшують інтерпретацію, викладення результатів дослідження. Для подання одномірного розподілу ознаки використовують гістограму (зображення за допомогою стовпчиків), або полігон (багатокутник) розподілу. їх побудова схожа, проте має деякі відмінності. Якщо на площині зобразити прямокутну систему координат (абсцис та ординат) та умовитись, що […]...
- Симетрія відносно прямої Геометрія Рух Симетрія відносно прямої Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок . Точка називається Симетричною точці X відносно прямої А. Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а. Очевидно, […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Координатна пряма Урок № 6 3 Тема. Координатна пряма Мета: сформувати уявлення про зміст поняття координатна пряма, координата точки і виробити вміння за готовими рисунками визначати координати вказаних точок та будувати на координатній прямій точки із вказаними координатами. Тип уроку: засвоєння нових знань. Хід уроку І. Перевірка домашнього завдання @ Ігровий момент “Хто найуважніший?” Учитель читає текст, […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Лабораторна робота № 1 “Визначення ЕРС і внутрішнього опору джерела струму” 1-й семестр ЕЛЕКТРОДИНАМІКА 2. Електричний струм УРОК 5/16 Тема. Лабораторна робота № 1 “Визначення ЕРС і внутрішнього опору джерела струму” Мета уроку: навчитися вимірювати ЕРС і внутрішній опір джерела струму. Тип уроку: урок контролю й оцінювання знань. Обладнання: джерело струму (гальванічний елемент, батарейка або блок харчування), амперметр, вольтметр, реостат, ключ, сполучні проводи. ХІД РОБОТИ 1. […]...
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
- Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Перетворення подібності та його властивості Урок 50 Тема. Перетворення подібності та його властивості Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач. Обладнання: моделі куба і тетраедра. Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення контрольних запитань № 9-11 та розв’язування задач № 23-25 (1). 2. Математичний диктант. При […]...