Квадрат і куб від’ємного числа
Урок № 8 4
Тема. Квадрат і куб від’ємного числа
Мета: повторити поняття квадрата та куба числа (степінь з натуральним показником) та з’ясувати властивості квадрата і куба від’ємного числа; продовжити роботу на удосконалення умінь виконувати додавання та множення раціональних чисел із використанням їх властивостей.
Тип уроку: застосування знань, вмінь, навичок.
Хід уроку
I. Перевірка домашнього завдання
Самостійна робота
Варіант 1
1. Обчисліть значення виразу, обравши зручний порядок дій: а) -5 – 49,02; б) –
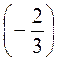-2
–
.2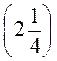. Розв’яжіть рівняння (2х + 0,2)(х – 0,5) = 0.
Варіант 2
1. Обчисліть, обравши зручний порядок дій: а) -8 – 36 – (-1,25); б)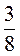 
–
–
–
.
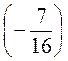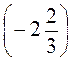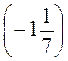2. Розв’яжіть рівняння (3x – 0,6)(х + 0,2) = 0.
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть:
А) (-2) – (-37) – (-5); б) (-25) – 106 – (-4); в) -1,23 – (-4) – (-5) – (-5); г) +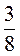 – (-8) – 
.
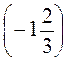2. Запишіть добуток у вигляді
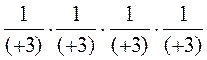; в)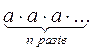 
.3. Обчисліть значення виразів: 52; 53; 22; (5 – 3)2; 52 – 32; 5 – 32; (5 – 3)3.
4. Яким буде знак добутку множників, якщо в ньому:
А) три множники від’ємні, а інші додатні;
Б) три додатні, два від’ємні;
В) два множники від’ємні, а інші додатні?
III. Засвоєння знань
@ Залежно від того, як було опрацьовано матеріал (квадрат і куб числа) у 5 класі, пояснення вчителя можуть бути більш або менш об’ємними (тобто, якщо учні забули зміст поняття “степінь”, то краще розпочати з пояснень того, що запис добутку однакових множників прийнято записувати у вигляді степеня, нагадати назви елементів цього запису, як обчислювати степінь, нагадати, що степені з показником 2 та 3 мають спеціальні назви – “квадрат” та “куб” числа).
Новими для знаннями учнів є властивість квадрата та куба від’ємного числа. Але якщо властивості добутків додатних чи від’ємних чисел (знак добутку залежить від кількості від’ємних множників) засвоєні учнями добре, то труднощів із засвоєнням цього моменту не повинно виникати.
Конспект 33 | |
Квадрат і куб від’ємного числа | |
Степінь додатного числа 1. а2 = аа – квадрат числа – число додатне! Якщо а < 0, то а2 > 0. a2 = (-a)2 (-1)2n = 1. 2. а3 = а – а – а – куб числа. Якщо а < 0, то а3 < 0 і а3 = -(-а)3; (-1)2n-1 = -1. | Приклад 1.(-3)2 = 32 = 9; 2. (-3)3 = -33 = – (3-3-3) = -27 |
@ Ще раз пояснити, що, обчислюючи значення квадрата або куба від’ємних чисел, треба спочатку визначити знак степеня, а потім підносити до степеня.
IV. Відпрацювання навичок
Усні вправи
1. Прочитайте: 32; (-3)2; 0,53; (-0,1)3; (-5 – 3)2; (-5 + 3)3.
2. Запишіть у вигляді степеня квадрата або куба: –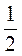
–
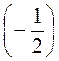; -0,3 – (-0,3) – (-0,3); 
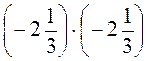; (-1) – (-1) – (-1).
3. Обчисліть значення степенів: (-1)2; (-1)3; (-2)3; (-2)2; (-0,2)2; (-0,2)3;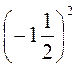 
; 
.
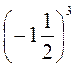Письмові вправи
Обчисліть:
1. а) (- 3)2; (- 3)4; (- 2)5; (- 1)10; б) (- 0,1)2; (- 0,2)3;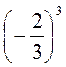 
; 
.
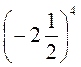2. а) 33 – (- 2)2; б) (0,5)2 – 33; в) (- 1 – 0,4)2 + 0,64; г) 2,52 – (- 3 + 2,5)2; д) (23 – (-5)2) – (-8); є) ((-0,01)3 – 0,23 ):0,1.
Додаткові вправи
3. а) Обчисліть: (-2,6)2 – (-3,2) –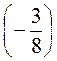 
+(-6,56).
Б) Знайдіть значення виразу 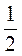B2 – 3с2, якщо b = -2, с = –.
В) Знайдіть значення виразу х2 – у2, якщо:
1) х = -6; у = -3; 2) х = –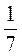
; у = –
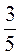; 3) х = 0,3; у = 0,1; 4) х = -0,7; у = -0,1; 5) х = -1
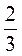; у = -1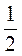; 6) х = 2
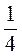; у = 1.
Г) Знайдіть пропущене число:
-7 |
| 49 |
-3 |
| 9 |
V. Підсумок уроку
Відомо, що 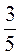– (-8) – 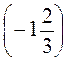,b > 0.
Які знаки (“>” або “<“) треба поставити замість *, щоб нерівності стали правильними: a2 * b; a * b3; b2 * b; b3 * а3; – а3 * b2.
VI. Домашнє завдання
Обчисліть:
1. а) (-5)2; (-3)3; (-4)4; (-1)7; б) (-0,4)2; (-0,1)3;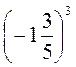 
.
2. а) (-2)3 – 32; б) (-2 + 0,5)3 – 22; в) (1 – 4)3: (-9)2.
3. Знайдіть добуток усіх цілих чисел які є розв’язками нерівності: а) -4 < х < 3; б) -50 < х < 100.
4. Обчисліть: а) 76 – 63 + 76 – 18 + 76 – 9; б) 637 – 36 – 165 – 36 + 36 – 28; в)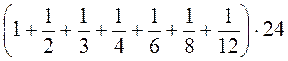 
.
(1 votes, average: 5.00 out of 5)
Loading...