Головна ⇒ 📌ГДЗ з математики ⇒ Лінійна функція

Лінійна функція

Розв’яжіть задачі

882. мал. 40.

883. 1) ні; 2) ні; 3) так.

884. 1) так; 2) ні; 3)так.

885. 1) ні; 2) ні; 3) так.

886. 1) ні; 2) ні; 3) так.

887. 1) ні; 2) ні; 3) так.

888. 1) 4; 2) -6; 3) 2/3.

889. 1) 3; 2) -0,5; 3) %.

890. 1) ні; 2) так; 3) ні.

891. 1) так; 2) ні; 3) ні.

892. 2) -3 = k • 0 + b; b = -3; b – від’ємне.

893. 1) 1,7 = 0 + b; b = 1,7 – додатне.

894. 1) гострий; k = 5 > 0; 2) гострий; k = 3 > 0; 3) тупий; k = -1,6 < 0.

895. 1) гострий; k = 2 > 0; 2) гострий; k = 0,5 > 0; 3) тупий; k = -1,2 < 0.

896. 1) х = -1; у = 3; x = 0; у = 2; x = 2,5; у = -0,5;

2) у = 0; х = 2; 3) x = -1,5; -1; -0,5; 4) x = 2,5; 3; 3,5; 5) –

6) функція спадна для будь-якого значення

х.

897. 1) х = -1; у = 0; х = 0; у = 1; х = 1; у = 2; х = 2,5; у = 2,5;

2) у = 0; х = -1; 3) х = 0; 1; 1,5; 4) x = -1,5; -2; -2,5;

5) для будь-якого значення х; 6) –

898. 1) А(1; 1); К(-1; 1) мал. 44; В(3; 3); L(-3; 3)мал. 44; С(4; 4); М(-4; 4) мал. 44; А(1; -1); K(-1; -1) мал. 45; В(3; -3); L(-3; -3) мал. 45; С(4; -4); М(-4; -4) мал. 45.

Ці точки мають протилежні абсциси.

2) оскільки в 1-му пункті; у = |х| задовольняє мал. 44; у = -|х| задовольняє мал. 45.

899. 1) (2; -2); 2) (-3; 3); 3) (-1; -1); 4) (7; -7); 5) (-1,25; 1,25); 6) (-4,1; 4,1).

900. 1) (-2; -2) є графіку функції y = -|х|;

2) (1; -1) є графіку функції у = -|х|;

3) (-1; 1) є графіку функції у = |х|;

4) (-1; -1) є графіку функції у = -|x|;

5) (-0,3; 0,3) є графіку функції у = |х|;

6) (1,5; 1,5) є графіку функції у = |х|.

901.

1) при х = -2, y = 2 • (-2) – 5 = -4 – 5 = -9;

2) при х = -1, у = 2 • (-1) – 5 = -2 – 5 = -7;

3) при х = 0,у = -5;

4) при х = 1, у = 2 • 1 – 5 = -3;

5) при х = 2, у = 2 • 2 – 5 = 4 – 5 = -1.

902. 1) при x = -2, y = -(-2) + 3 = 2 + 3 = 5;

2) при х = -1, y = -(-1) + 3 = 1 + 3 = 4;

3) при х = 0, у = 0 + 3 = 3;

4) при х = 1, у = -1 + 3 = 2;

5) при х = 2, y = -2 + 3 = 1.

Лінійна функція

905. 1) -3 ≠ 5 • 1 – 2; -3 ≠ 3. А не належить графіку функції;

2) 3 = 5 • 1 – 2; 3 = 3; В належить графіку функції;

3) 2 ≠ 5 • 0 – 2; 2 ≠ -2; С не належить графіку функції;

4) -7 = 5 • (-1) – 2; -7 = -7; D належить графіку функції.

906. 1) -3 ≠ 1 – 2; -3 ≠ -1; М не належить графіку;

2) 3 ≠ -1 – 2; 3 ≠ -3; N не належить графіку;

3) 4 ≠ -2 – 2; 4 ≠ -4; Р не належить графіку;

4) 0 = 2 – 2; 0 = 0; R належить графіку функції.

907. 1) (0; 7); (1; 5); (-1; 9); 2) (0; -1,5); (1; -1); (2; 0,5).

908. 1) 1 ≠ 4 – 3 • (-1); 1 ≠ 4 + 3; 1 ≠ 7; К не належить графіку;

2) 1 = 4 – 3 • 1; 1 = 4 – 3; 1 = 1; L належить графіку;

3) 2 ≠ 4 – 3 • 2; 2 ≠ 4 – 6; 2 ≠ -2; М не належить графіку;

4) -10 ≠ 4 – 3 • (-2); -10 ≠ 4 + 6; -10 ≠ 10; N не належить графіку.

909. 1) у = х – 1; графік – гіряма(0; -1); (1; 0)

Лінійна функція

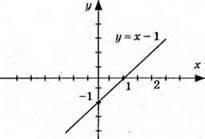
2) у = – х – 1; графік – пряма (0; -1); (1; -2)

Лінійна функція

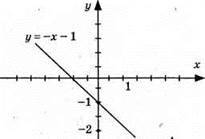
3) у = – х + 1; графік – пряма (0; 1); (1; 0)

Лінійна функція

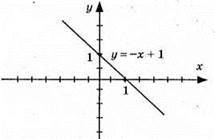
4) y = х + 1; графік – пряма (0; 1); (1; 2)

Лінійна функція

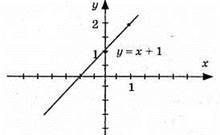
910. 1) у = 2х + 1, графік – пряма (0; 1); (1; 3)

Лінійна функція

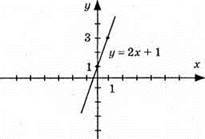
2) у = -2x + 1, графік – пряма (0; 1); (1; -1)

Лінійна функція

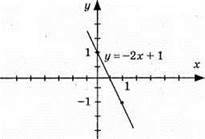
3) у = -2x – 1, графік – пряма (0; -1); (1; -3)

Лінійна функція

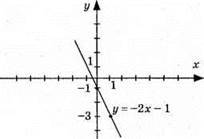
4) у = 2х – 1, графік – пряма (0; -1); (1; 1)

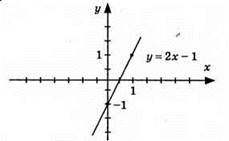
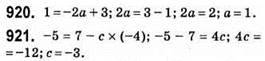
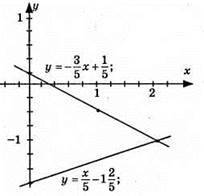
Лінійна функція

Лінійна функція

Лінійна функція

922. 1) у = 0,5x – 1,5, графік – пряма; (0; -1,5); (2; -0,5); а) у = 0, при х = 3; б) у > 0, при х > 3; в) у < 0, при х < 3;

Лінійна функція

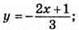2) Лінійна функція графік – пряма; (1; -1); (0; -1/3); a) у = 0, при x = -1/2; б) y > 0, при х < -1/2; в) у < 0, при х > -1/2;

Лінійна функція

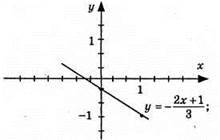
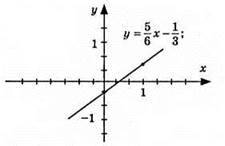
3) 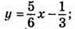Лінійна функція графік – пряма; (1; 1/2); (0; -1/3); а) у = 0, при х = 2/5; б) у > 0, при х > 2/5; в) y < 0, при х < 2/5.

Лінійна функція

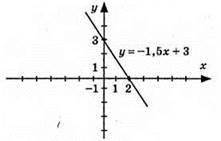
923. 1) y = -1,5х + 3, графік – пряма; (0; 3); (2; 0); а) у = 0, х = 2; б) у > 0, при х < 2; в) у < 0, при х > 2;

Лінійна функція

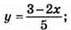2) Лінійна функція графік – пряма; (1,5; 0); (1; 1/5); а) у = 0, при х = 1,5; б) у > 0, при х < 1,5; в) у < 0, при x > 1,5;

Лінійна функція

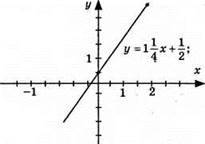
3) 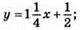Лінійна функція графік – пряма; (0; 1/2); (2; 3); а) у = 0, при х = -2/5; б) y > 0, при x > -2/5; в) у < 0, при x < -2/5.

Лінійна функція

924. 1) y = 2x – 0,5, графік – пряма; (0; -0,5); (0,5; 0,5); у = -0,5x + 2, графік – пряма; (0; 2); (2; 1); точка перетину: (1; 1,5);

Лінійна функція

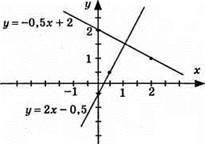
2) 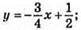Лінійна функція графік – пряма; (0; 1/2); (2; -1);

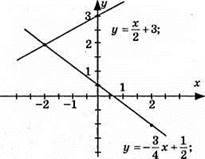
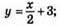Лінійна функція графік – пряма; (0; 3); (6; 6); (-2; 2); точка перетину: (-2; 2).

Лінійна функція

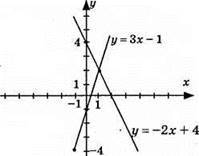
925. 1) у = 3x – 1, графік – пряма; (0; -1); (-1; -4)

У = -2х + 4, графік – пряма; (0; 4); (1; 2); точка перетину: (1; 2);

Лінійна функція

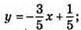2) Лінійна функція графік – пряма; (0; 1/5); (1; -2/5);

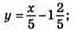Лінійна функція графік – пряма; (2; -1); 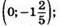Лінійна функція точка перетину: (2; 2).

Лінійна функція

Лінійна функція

927. 1) у – будь-яке значення; 2) у ≥ 0; 3) у ≥ 2; 4) y ≥ -3.

928. 1) у – будь-яке значення; 2) у ≥ -5.

929. 1. а) (0; 1) належить мал. 46; б) (0; -1) належить мал. 47;

2. а) А(1; 2); K(-1; 2); В(3; 4); L(-3; 4) з мал. 46; В(3; 2); L(-3; 2); С(4; 3); М(-4; 3) з мал. 47. Ці точки мають протилежні абсциси; б) Аналогічно пункту а);

3. а) у = |х| + 1 мал. 46; б) y = |X| – 1 мал. 47.

930. 1. а) (0; 1) мал. 49; б) (0; -1) мал. 48;

2. а) мал. 48: K(-1; -2); А(1; -2); L(-3; -4); В(3; -4);

Мал. 49; L(-2; -1); А(2; -1); М(-4; -3); В(4; -3).

Ці точки мають протилежні абсциси;

Б) див. пункт а);

3. а) у = -|х| + 1 мал. 49; б) у = -|х| – 1 мал. 48.

931. -3 = – а + b; -3 = – a + 2; а = 2 + 3; а = 5 і 2 = 0 + b; b = 2.

932. 1) у = 2x + 3; 2) у = x.

933. HСД(42; 91) = 7;

Лінійна функція

K = 7; -10 = 7 • (-1) + b; -10 + 7 = b; b = -3.

934. НСД(96; 112) = 2 • 2 • 2 • 2 = 16;

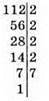
Лінійна функція Лінійна функція

А = 16; а = 16. 14 = 16 • 1 + с; с= 14 – 16; с = -2.

935. 1) у = x – 2, графік – пряма; (-1; -3); (-2; -4); у = 3х, графік – пряма; (0; 0); (1; 3). у = 2х + 4, графік – пряма (2; 8); (3; 10).

Лінійна функція

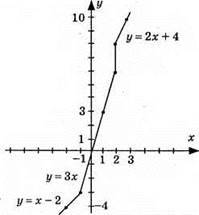
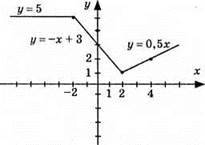
2) у = – х + 3, графік – пряма; (0; 3); (1; 2); у = 0,5x, графік – пряма; (2; 1); (4; 2) у = 5, графік – пряма, паралельна осі 0х;

Лінійна функція

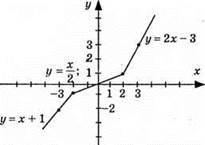
3) у = х + 1, графік – пряма; (-2; -1); (-3; -2); y = x/2; графік – пряма; (-2; -1); (0; 0); у = 2х – 3, графік – пряма (2;1); (3; 3);

Лінійна функція

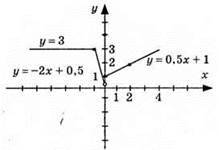
4) у = 3; графік – пряма, паралельна осі 0x; у = -2х + 0,5; графік – пряма; (-1; 2,5); (-0,5; 1,5); у = 0,5x + 1; графік – пряма; (0; 1); (2; 2).

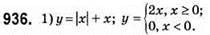
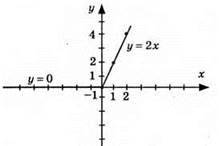
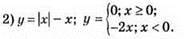
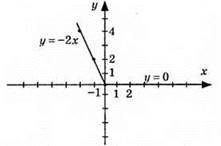
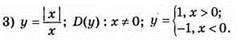
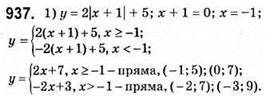
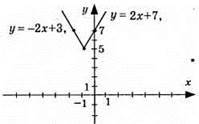
Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

Лінійна функція

2) у = |x – 1| + |x – 2|; нулі функції x = 1; x = 2;

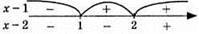
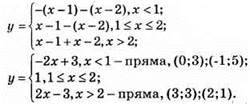
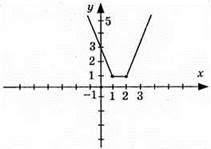
Лінійна функція

Лінійна функція

Лінійна функція

3) у = |x – 3| – |1 – x|; нулі функції x = 3; x = 1;

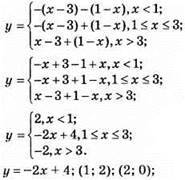
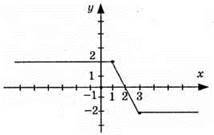
Лінійна функція

Лінійна функція

Лінійна функція

4) у = 2|х – 3| – 3|x + 2|; нулі функції: x = 3; x = -2;

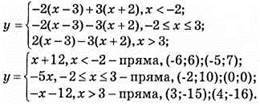
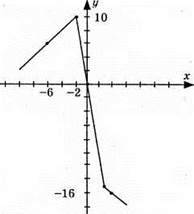
Лінійна функція

Лінійна функція

Лінійна функція

938. 1) |у| = х – 3; х – 3 ≥ 0; х ≥ 3; у = х – 3 або у = – х + 3; у = х – 3 – пряма, (3; 0); (4; 1); у = – х + 3, графік – пряма, (3; 0); (4; -1);

Лінійна функція

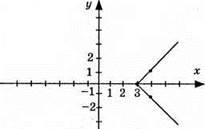
2) |x| + |у| = 1; х ≥ 0, у ≥ 0, х + у = 1, y = 1 – х; (0; 1); (2; -1);

Х < 0, у > 0, – х + у = 1, у = 1 + х; (0; 1); (-1; 0);

Х > 0, у < 0, х – у = 1, у = х – 1; (1; 0); (2; 1);

Х < 0, у < 0, – x – у = 1, у = – х – 1; (0; -1); (1; -2);

Лінійна функція

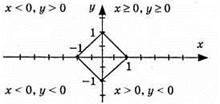
3) |x| – |у| = -1; x ≥ 0, у ≥ 0, x – у = -1, y = х + 1; (0; 1); (1; 2);

X < 0, у > 0, – x – у = -1, y = – х + 1; (0; 1); (1; 0);

Х < 0, у < 0, – х + у = -1, у = x – 1; (0; -1); (1; 0);

Х > 0, у < 0, х + у = -1, у = -1 – х; (0; -1); (1; -2).

Лінійна функція

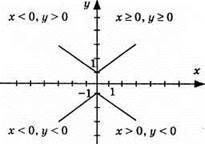
Ці зображення не можуть бути графіком якоїсь функції, бо одному значенню х (аргументу) відповідають 2 різні значення у (функції).

Застосуйте на практиці.

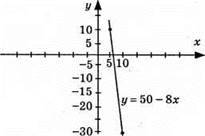
939. у = 50 – 8х; (графік – пряма); у – сума грошей після витрат; х – дні тижня; точки для побудови: (10; -30); (5; 10).

Лінійна функція

940. у = 1,7x, x – кількість халатів; у – загальна кількість погонних метрів;

1) у = 1,7 • 5 = 8,5 (м); 2) у = 1,7 • 8 = 13,6 (м); 3) у = 1,7 • 25 = 42,5 (м); 4) у = 1,7 • 100 = 170 (м).

Задачі на повторення.

Лінійна функція

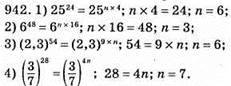
943. Нехай x – дане число, тоді:

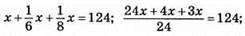
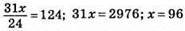Лінійна функція

Лінійна функція – шукане число.

944. Число 1350.

945. 40 % від 10 см = 10 • 0,4 = 4 см

10 см + 4 см = 14 см – сторона прямокутника після збільшення;

40 % від 15 см = 15 • 0,4 = 6 см

15 см – 6 см = 9 см – сторона після зменшення;

Р = 2 • (10 + 15) = 50 см – периметр даного прямокутника.

Р = 2 • (9 + 14) = 46 см – периметр зміненого прямокутника;

100 % – (46 : 50 • 100 %) = 100 % – 92 % = 8 %.

Периметр прямокутника на 8 % зменшився.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...

  2. Лінійна функція, її графік і властивості 849. Лінійною функцією є: 850. Прямою пропорційністю є функції: 851. y = 6x – 5 X -3 -2 -1 0 1 2 3 У -23 -17 -11 -5 1 7 13 852. 1) y = -2x + 5 Якщо x = -4, то у = -2 • (-4) + 5 = 13. Якщо x = […]...

  3. Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...

  4. ЛІНІЙНА ФУНКЦІЯ РОЗДІЛ 4 ФУНКЦІЇ &17. ЛІНІЙНА ФУНКЦІЯ У дослідженні реальних процесів і явищ функції відіграють особливу роль – математичних моделей. Найбільш важливим функціям математики дають власні назви. Однією з них є лінійна функція. Розглянемо приклади, що приводять до лінійної функції. Нехай 1 кг цукерок коштує 25 грн. Тоді залежність між масою т цукерок та їх вартістю […]...

  5. Лінійна функція та її графік Урок № 66 Тема. Лінійна функція та її графік Мета: сформувати свідоме розуміння учнями взаємозв’язку між взаємним розташуванням графіків двох лінійних функцій та співвідношенням їх кутових коефіцієнтів; виробити вміння: за даними рівняннями лінійних функцій робити висновки щодо взаємного розташування графіків; знаходити аналітичним способом координати точки перетину графіків двох лінійних функцій. Тип уроку: застосування знань, умінь […]...

  6. Лінійна функція, її графік та властивості Розділ 2. ФУНКЦІЇ & 21. Лінійна функція, її графік та властивості Приклад 1. Маса одного цвяха 4 г, а маса порожнього ящика – 600 г. Залежність між масою т (у г) ящика із цвяхами і кількістю цвяхів у ньому, що дорівнює х (х – натуральне число), можна задати формулою: M = 4x + 600. Приклад […]...

  7. Лінійна функція, її графік та властивості Урок № 65 Тема. Лінійна функція, її графік та властивості Мета: ознайомити учнів із “особливими випадками” лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (див. попередній урок) […]...

  8. Пряма пропорційність Розв’яжіть задачі 946. 1) ні; 2) так; 3) ні; 4) ні. 947. 1) ні; 2) ні; 3) ні; 4) ні; 5) так. 948. малюнок 57. 949. 1) ні; 2) так; 3) ні. 950. 1) k = 4; 2) k = -0,7; 3) k = 2/3. 951. 1) ні; 2) так; 3) ні. 952. 1) ні; […]...

  9. Координатна площина. Графік функції 824. 1) абсциса точки А дорівнює -3; 2) ордината точки А дорівнює 7. 825. Точка А в II чверті; В в IV чверті; С в IV чверті; D в II чверті; Е в І чверті; F у III чверті; K у II чверті; L у III чверті. 826. 1) ні; 2) ні; 3) ні. 827. […]...

  10. Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...

  11. Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...

  12. Функція у = х2, її властивості, графік Урок № 33 Тема. Функція у = х2, її властивості, графік Мета: домогтися засвоєння учнями властивостей функції у = х2 та виду і властивостей її графіка та способу застосування графіка функції у = х2 для графічного розв’язання рівнянь виду х2 = а; формувати вміння відтворювати зміст вивчених понять, відпрацювати навички роботи з графіком функції. Тин […]...

  13. Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...

  14. Функція y=k/x, її властивості і графік Урок № 30 Тема. Функція , її властивості і графік Мета: закріпити знання учнів щодо означення й основних властивостей функції та її графіка; сформувати сталі вміння застосувати набуті знання в розв’язуванні завдань базового, середнього та достатнього рівнів, зміст яких відповідає програмовим вимогам; поглибити знання учнів про сферу застосування властивостей функції (графіка функції) уявленням про графічний […]...

  15. Функції Урок № 68 Тема. Функції Мета: виявити рівень засвоєння обов’язкових знань та вмінь з теми “Функція”, передбачених програмою з математики та ступінь сформованості навичок. Тип уроку: контроль знань та вмінь. Форма проведення: тематична контрольна робота. Хід уроку І. Перевірка домашнього завдання II. Умова тематичної контрольної роботи Варіант 1 Варіант 2 1?. Функцію задано формулою У […]...

  16. Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...

  17. Функція y=vx, її властивості і графік Урок № 44 Тема. Функція , її властивості і графік Мета: домогтися засвоєння учнями змісту основних властивостей функції ; сформувати вміння відтворювати вивчені властивості, а також використовувати їх у розв’язуванні програмових задач. Тип уроку: засвоєння знань та вмінь. Наочність та обладнання: опорний конспект “Функції”. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання На цьому […]...

  18. Показникова функція, її графік і властивості УРОК 43 Тема. Показникова функція, її графік і властивості Мета уроку. Засвоєння учнями поняття показникової функції, її властивостей і графіка. Обладнання. Таблиця “Показникова функція”. І. Аналіз контрольної роботи II. Повідомлення теми уроку III. Сприймання і усвідомлення нового матеріалу Функція виду у = ах, де а > 0, а? 1, називається показниковою (з основою а). Усне […]...

  19. Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...

  20. Лінійна швидкість – Кінематика 5. Механіка 5.1. Кінематика 5.1.28. Лінійна швидкість Лінійна швидкість точки – це швидкість, що вимірюється відношенням довжини дуги, по якій рухається точка, до проміжку часу, за який цю дугу пройдено. Формула: Під час руху по колу:...

  21. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...

  22. 5 вправа 648-769 648. х – довжина сторони квадрата; S – площа квадрата; Х – незалежна змінна; у – залежна змінна. S = х2. 649. у = 5х; х – аргумент; у – функція. А) Якщо х = 2, то y = 5 • 2 = 10; якщо х = -1, то у = 5 • (-1) = […]...

  23. Степенева функція УРОК 41 Тема. Степенева функція Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками. І. Перевірка домашнього завдання 1. Перевірити наявність виконаного домашнього завдання. 2. Розв’язування вправ. А) Обчислити . Відповідь: 5. Б) Спростити вираз . Відповідь: ab. В) Спростити вираз . Відповідь: 2a. II. Сприймання і усвідомлення матеріалу про степеневу функцію Степеневою […]...

  24. Геометричні фігури, точка, пряма, промінь Розділ 1. Елементарні геометричні фігури та їхні властивості § 1. Геометричні фігури, точка, пряма, промінь 1. 1) Прямій а належать точки А, В, С. 2) Прямій b належать точки Р i В. 3) Прямій а і прямій b належить точка В. 4) Точки А і С належать прямій а, але не належать прямій b. 5) […]...

  25. Квадратична функція – Функції та графіки Математика – Алгебра Функції та графіки Квадратична функція Квадратним тричленом називається многочлен виду , де x – змінна, a, b і c – деякі числа, причому . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння . Теорема. Якщо і – корені […]...

  26. Логарифмічна функція, її графік і властивості УРОК 56 Тема. Логарифмічна функція, її графік і властивості Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправ № 13, 15, 20. 2. Розв’язування вправ, аналогічних домашнім. А) Обчисліть: ; . =====–=. ====–= 5. Б) Обчисліть . ==== 52 – 3-2 = 25 […]...

  27. Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...

  28. Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...

  29. Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...

  30. ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ ФУНКЦІЇ Цілі: – навчальна: сформувати поняття функції, аргументу та значення функції; домогтися засвоєння способів задання функції; сформувати вміння розв’язувати задачі, які передбачають застосування цих понять; – розвивальна: формувати культуру усного та писемного мовлення; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, працьовитість; Тип уроку : засвоєння нових знань, […]...

  31. Функція y=ax2+bx+c, її властивості та графік УРОК № 23 Тема. Функція , її властивості та графік Мета уроку: закріпити знання учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції. Дослідити властивості квадратичної функції та узагальнити ці спостереження, доповнивши ними знання про властивості квадратичної функції. Закріпити вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям віток […]...

  32. Графік функції Урок № 63 Тема. Графік функції Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”. Хід уроку I. Організаційний момент Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці. II. Перевірка домашнього […]...

  33. Завдання для перевірки знань за курс алгебри 7 класу 1. 1) х – 2 = 5; 7 – 2 = 5; 5 = 5; 7 – корінь рівняння; 2) 56 : х = 6; 56 : 7 = 8; 8 ≠ 6; 7 – не є корінь рівняння. 2. 1) p4 • p3 = р7; 2) t9 : t5 = t4. 3. 1) х […]...

  34. Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...

  35. ПРЯМА ПРОПОРЦІЙНІСТЬ РОЗДІЛ 4 ФУНКЦІЇ &18. ПРЯМА ПРОПОРЦІЙНІСТЬ Ви знаєте, що залежність вартості р цукерок від їх кількості т, якщо їх ціна становить 25 грн за кілограм, можна виразити формулою р = 25m, або в загальному вигляді у = kх. Така залежність є особливим випадком лінійної функції y = Kх + b, коли b = 0, a […]...

  36. Зв’язки між величинами. Функція 753. P = 3а – залежність функціональна. 754. S = а2 – залежність функціональна. 755. S = 60t – залежність функціональна; t – аргумент функції. 756. V = 300 – 2t – функція, t – аргумент, 0 ≤ t ≤ 150. V – область значень, 0 ≤ V ≤ 300. Область визначення: від 0 до […]...

  37. Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...

  38. Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....

  39. Що таке функція 783. 1) так; 2) ні; 3) ні. 784. 1) так; 2) ні; 3) ні. 785. у = 2x + 3. Область визначення (D(f)): будь-яке значення аргумента; Область значень (Е(f)): будь-яке значення функції. 786. у = х+1 X 1 -1 2 У 2 0 3 D(f) = D(y): -1; 1; 2; Е(у): 0; 2; 3. 787. […]...

  40. Виробнича функція. Двофакторна виробнича функція Кобба УРОК 10 Виробнича функція. Двофакторна виробнича функція Кобба – Дугласа: економічний зміст та графічна інтерпретація Мета уроку: визначити функціональну залежність між факторами й обсягом виробництва; подати графічну й економічну інтерпретацію двофакторної виробничої функції; формувати в учнів уявлення про підприємство як відкриту й багатоелементну систему. Основні поняття: функція, фактори виробництва, виробнича функція, ізокванта. Тип уроку: комбінований. […]...

Ви зараз читаєте: Лінійна функція
«
»