ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ
РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
&21. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ
Ви знаєте, що рівняння можуть бути як з однією змінною, так і з двома змінними. Наприклад, 5(2х + у) = 15 – це рівняння з двома змінними х і у.
На відміну від рівняння з однією змінною, рівняння з двома змінними може задовольняти лише пара значень змінних, які входять до нього. Наприклад, рівняння 5(2х + y) = 15 задовольняють такі пари значень х і у, як: -1 і 5, 0 і 3, 2 і -1 тощо. Узагалі для даного рівняння таких пар чисел – безліч. Справді, з даного рівняння випливає,
Зрозуміло, що пара чисел, яка задовольняє рівняння з двома змінними, є упорядкованою. Справді, рівняння 5(2х + у) = 15 задовольняє, наприклад, пара значень змінних х = 2 і у = -1:
5 ∙ (2 ∙ 2 + (-1)) = 15.
А от пара значень змінних х = -1 і у = 2 не задовольняє дане рівняння:
5 ∙ (2 (-1) + 2) ≠ 15.
Упорядковану пару чисел а і b коротко записують так: (а; b).
Зверніть увагу:
Для рівнянь із двома (чи більше) змінними термін “корінь”
Запам’ятайте!
Упорядкована пара чисел, що задовольняє рівняння з двома змінними, називається розв’язком цього рівняння.
Щоб описати всі розв’язки рівняння з двома змінними, шукають так званий загальний розв’язок, тобто формулу,
Яка виражає залежність однієї змінної від іншої в цьому рівнянні. Наприклад, для рівняння 5(2x + у) = 15 загальний розв’язок має вигляд: 2х + у = 3 або, що те саме, у = -2х + 3 чи x = – Y +
Y + .
.
Серед рівнянь із двома змінними виділяють особливий їх вид – лінійні рівняння.
Рівняння виду ах + by + с = 0, де х і у – змінні, а, b і с – деякі числа, називається лінійним рівнянням із двома змінними.
Числа а, b і с називають коефіцієнтами лінійного рівняння з двома змінними. Число с інакше називають вільним членом даного рівняння.
? Чи можна вважати лінійним рівнянням із двома змінними рівняння виду ах + by = d? Так. Це інша форма запису лінійного рівняння з двома змінними.
Залежно від того, яких значень набувають коефіцієнти а, b і с, лінійне рівняння з двома змінними ах + by + с = 0 може мати розв’язки або не мати їх.
Рівняння aх + bу + с= 0 не має розв’язків лише тоді, коли а = 0, b = 0, а вільний член с ≠ 0. Справді, за таких значень коефіцієнтів дане рівняння набуває вигляду: 0х + 0 ∙ y + с = 0. Але не існує такої пари значень х і у, яка б задовольняла це рівняння.
В усіх інших випадках рівняння aх + bу + с= 0 має безліч розв’язків. Проте лише тоді, коли а ≠ 0 і b ≠ 0, значення х і у залежать одне від одного. У цьому випадку загальний розв’язок рівняння ax + by + c = 0 можна подати або як залежність у від х, або як залежність х від у: y = –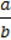 X –
X – 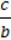 або х = –
або х = – Y –
Y –  .
.
Якщо хоча б один із коефіцієнтів а чи b дорівнює 0, то відповідно або у набуває, лише одного числового значення, або х, а друга змінна може набувати будь-яких значень:
Якщо а = 0, то у = 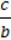 , х – будь-яке число;
, х – будь-яке число;
Якщо 5 = 0, то х =  , у – будь-яке число.
, у – будь-яке число.
Якщо всі три коефіцієнти рівняння ах + bу + с = 0 дорівнюють 0, то це рівняння задовольняє будь-яка пара чисел і таких пар – безліч.
Лінійні рівняння з двома змінними, що мають одні й ті самі розв’язки, називають рівносильними. Рівняння з двома змінними, які не мають розв’язків, також вважають рівносильними. Властивості рівносильності лінійних рівнянь із двома змінними аналогічні таким самим властивостям рівнянь з однією змінною. Сформулюйте їх самостійно.
Шукаючи розв’язки лінійного рівняння з двома змінними, використовують властивості рівносильності рівнянь і тотожні перетворення виразів.
Задача 1. Знайдіть три розв’язки рівняння 5х + 2у – 11 =0.
Розв’язання. Задачу можна розв’язати двома способами.
Спосіб 1. Оберемо довільно три значення змінної х, а потім знайдемо значення змінної у, розв’язуючи відповідне рівняння:
1) нехай х = 0, тоді 5 ∙ 0 + 2у – 11 = 0, звідси 2у = 11 і у = 5,5;
2) нехай х = 4, тоді 5 ∙ 4 + 2у – 11 = 0, звідси 2у = -9 і у = -4,5;
3) нехай х = -1, тоді 5 ∙ (-1) + 2у -11 = 0, звідси 2у = 16 і у = 8.
Отже, серед розв’язків даного рівняння є пари чисел: (0; 5,5), (4;-4,5) і (-1; 8).
Спосіб 2. Знайдемо загальний розв’язок даного рівняння. Для і цього виразимо, наприклад, у через х:
5х + 2у -11 = 0,
2у = -5X + 11, | :2
У = -2,5х + 5,5.
Тоді:
1) якщо х = 0, то у = -2,5х + 5,5 = -2,5 ∙ 0 + 5,5 = 5,5;
2) якщо х = 4,то у = -2,5х + 5,5 = -2,5 ∙ 4 + 5,5 = -4,5;
3) якщо x = -1,тo у = -2,5x + 5,5 = -2,5 ∙ (-1) + 5,5 = 8.
Отже, серед розв’язків даного рівняння є пари чисел: (0; 5,5), (4; -4,5) і (-1; 8).
Зверніть увагу:
Щоб знайти загальний розв’язок лінійного рівняння з двома змінними х і у, достатньо розв’язати це рівняння відносно однієї з його змінних:
– розв’язати відносно у рівняння ах + bу + с = 0 – означає перетворити дане рівняння так, щоб усамітнити змінну у, тобто виразити у через я;
– розв’язати відносно х рівняння aх + bу + с = 0 означає перетворити дане рівняння так, щоб усамітнити змінну х, тобто виразити х через у.
Рівняння з двома змінними, так само, як і рівняння з однією змінною, можна поділити на види і за іншою основою – залежно від степеня многочлена, який породжує дане рівняння. Якщо многочлен першого степеня, то і відповідне рівняння є рівнянням першого степеня.
? Чи кожне лінійне рівняння з двома змінними є рівнянням першого степеня? Ні. Наприклад, лінійні рівняння 0 ∙ х + 0 ∙ у + с = 0 і 0 ∙ x + 0 ∙ у + 0 = 0 не є рівняннями першого степеня.
Дізнайтеся більше
1. “Коротка книга поповнення і протиставлення” (від арабського кітаб аль-джебр валь-мукабале) – відома книга арабського вченого Мухаммеда ібн Муси аль-Хорезмі, від назви якої започаткували термін “алгебра”.
Ця книга є важливою віхою становлення алгебри як науки про розв’язування рівнянь. Вона століттями визначала характер алгебри як практичної науки. Книга ділиться на три частини: рівняння першого та другого степенівіз вправами; практична тригонометрія; розв’язування задач на поділ спадщини. На малюнку 63 наведено першу сторінку книги. Аль-Хорезмі в цій книзі започаткував традицію поводитися з рівняннями так, як торговець поводиться з гирями на терезах. Він запропонував рівняння розглядати як рівність мас на обох шальках терезів. А для них можна проводити такі перетворення: докладати на обидві шальки терезів гирі однакові маси або знімати їх.

Мал. 63
2. Розглядаючи особливості лінійних рівнянь з однією чи двома змінними, ми записували такі рівняння в загальному вигляді: ах + b = 0 та ах + by + с = 0. їх коефіцієнти а і b та а, b і с ми вважали деякими числами (а не змінними!), які можуть набувати будь-яких значень. Якщо змінювати значення коефіцієнтів у загальному рівнянні, щоразу будемо отримувати нове конкретне рівняння, але того самого вигляду: 3х + 1 =0, -2х + 5 = 0 чи0,25х – 8 = 0 тощо. У математиці такі фіксовані, але невідомі для даного загального рівняння числа, інакше називають параметрами. Отже, будь-яке рівняння, записане в загальному вигляді, можна вважати рівнянням з параметрами (одним чи кількома).
Розв’язати рівняння з параметрами означає: 1) знайти всі набори значень параметрів (їх називають контрольними значеннями параметрів), за яких дане рівняння або має розв’язок, або не має його, або має якісь особливості розв’язку, що відрізняють цей розв’язок від інших розв’язків; 2) для кожного значення параметра (набору значень параметрів, якщо параметрів – кілька) знайти всі корені або вказати, за яких значень параметра рівняння коренів не має. Отже, розв’язування рівняння з параметрами розбивають на кілька випадків (залежно від контрольних значень параметрів), щоб для кожного з них записати відповідь через параметри однозначно. Розглянемо приклади.
Задача 1. Розв’яжіть рівняння ах = 10 відносно х.
Розв’язання. У рівнянні ах = 10 параметр а є коефіцієнтом біля змінної х. Тому, якщо а = 0, то рівняння стане особливим – воно не матиме розв’язку. Справді, у цьому випадку дане рівняння набуде вигляду: 0 ∙ х = 10. А таке рівняння не має коренів.
Для всіх інших значень параметра а розв’язок існує і його можна подати в загальному вигляді: х =  . Коротко розв’язання задачі можемо записати так.
. Коротко розв’язання задачі можемо записати так.
1. Нехай а = 0, тоді 0 ∙ х = 10 – коренів немає.
2. Нехай а ≠ 0, тоді х =  – корінь рівняння.
– корінь рівняння.
Відповідь: ЯКЩО а ≠ 0, то х =  ; якщо а = 0, то коренів немає.
; якщо а = 0, то коренів немає.
Задача 2. За яких значень параметра а рівняння (a – 2)у = a2 – 4 має безліч коренів?
Розв’язання. Рівняння (а – 2)у – = а2 – 4 є лінійним рівнянням з однією змінною у. Таке рівняння матиме безліч коренів, якщо набуде вигляду 0 ∙ у = 0 Отже, для розв’язання задачі достатньо розглянути один випадок, коли одночасно а – 2 – 0 i а2 – 4 = 0. Із першої рівності отримуємо: а = 2. Другу рівність перетворимо так: (а – 2)(а + 2) = 0, звідси дістанемо: а = 2 або а = -2. Рівності a – 2 = 0 і a2 – 4 = 0 справджуються одночасно лише тоді, коли а = 2. Справді, якщо а = -2, то задане рівняння набуває вигляду: -4 ∙ у = 0. А таке рівняння має єдиний корінь – 0, що не передбачено вимогою задачі. Отже, лише за a = 2 рівняння (а – 2)у = a2 – 4 має безліч коренів.
Відповідь: а =2.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке лінійне рівняння з двома змінними?
2. Що є розв’язком лінійного рівняння з двома змінними?
3. Скільки розв’язків може мати лінійне рівняння з двома змінними?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
1055. Назвіть коефіцієнти лінійного рівняння з двома змінними:
1)2х + 3y – 16 = 0;
2)5х – у + 12 = 0;
3)х – 2у – 1 = 0;
4)5х – 15y = 0.
Яке число є вільним членом даного рівняння?
1056. Чи є лінійним рівнянням із двома змінними таке рівняння:
1) 3х + 4y = 1;
2) 2у + 2 = 0;
3) 3x –  Y + 5 = 0;
Y + 5 = 0;
4) 3х – 8 = 0?
Відповідь поясніть.
1057. Чи є розв’язком рівняння х – у + 5 = 0 є пара чисел:
1) (-2; 3); 2) (0; -5); 3) (1; 4); 4)(0; 5)?
1058. Складіть лінійне рівняння з двома змінними, якщо відомі його коефіцієнти:
1) а = 8, b = -5, с = 4; 3) a = 1, b =- 1, с = -1;
2) a =  , b = -0,2, с = 2,5; 4) а = 2, b = -5, с = 0.
, b = -0,2, с = 2,5; 4) а = 2, b = -5, с = 0.
1059. Складіть лінійне рівняння з двома змінними, якщо відомі його коефіцієнти:
1) а = -4, b = 2, с = 0; 2) а = 5, b = -1, с = 1.
1060. Складіть лінійне рівняння з двома змінними, розв’язком якого є пара чисел:
1)(2; 8); 2) (-1; 5).
1061. Складіть лінійне рівняння з двома змінними, розв’язком якого є пара чисел (-4; 0).
1062. Виразіть змінну у через змінну х у рівнянні:
1) 3х + у-5 = 0; 3) 3х – 3у + 10 = 0;
2) -4х + 2у + 7 = 0; 4)3х –  у – 2 = 0
у – 2 = 0
Знайдіть три будь-які розв’язки цього рівняння.
1063. Виразіть змінну у через змінну х у рівнянні:
1) 4х + у + 7 = 0; 2) 16х – 4у + 5 = 0.
Знайдіть два будь-які розв’язки цього рівняння.
1064. Запишіть загальний розв’язок даного рівняння, розв’язавши його відносно х:
1) х + 2у – 8 = 0; 3)-8х – 16y + 2,4 = 0;
2) 2х – 2у + 7 = 0; 4)4х – 1 У – 2 = 0.
У – 2 = 0.
Знайдіть три будь-які розв’язки цього рівняння.
1065. Запишіть загальний розв’язок даного рівняння, розв’язавши його відносно у:
1)х – 5у + 12 = 0; 2) -7х – 14у + 1 = 0.
= 0.
Знайдіть два будь-які розв’язки цього рівняння.
1066. Знайдіть три будь-які розв’язки рівняння:
1) 4х + 2(у – 1) = 0; 3) 5(2y – х) – 8 = 0;
2) 6(х + 2) – 2у + 12 = 0; 4) 9(y –  Y) + 6 = 0.
Y) + 6 = 0.
Розв’яжіть задачу двома способами.
1067. Знайдіть два будь-які розв’язки рівняння:
1) 2(2х – у) -3 = 0; 2)8х – 5(у – 8х – 5(y –  ) = 0) = 0.
) = 0) = 0.
Розв’яжіть задачу двома способами.
1068. Розв’язком рівняння 4х + 0,1у – 1,3 = 0 є пара чисел (1; b). Знайдіть b.
1069. Розв’язком рівняння 0,5х + 2у – 1,5 = 0 є пара чисел (а; -1). Знайдіть а.
1070. Серед розв’язків рівняння 2х + у = 12 знайдіть таку пару, яка б складалася із: 1) двох однакових чисел; 2) двох чисел, одне з яких удвічі більше за інше.
1071. Серед розв’язків рівняння х – 3у = 16 знайдіть таку пару, яка б складалася із: 1) двох протилежних чисел; 2) двох чисел, одне з яких утричі менше від іншого.
1072. Складіть лінійне рівняння з двома змінними, розв’язок якого має вигляд:
1) (х; 5х – 1); 2) (у; 2у + 4).
1073. За якого значення п пара чисел (-2; 1) є розв’язком рівняння:
1) 2х + nу – 4 = 0; 3) х + 0,5у – n = 0;
2) nх + 3у – 2,5 = 0; 4) 5х + (n – 1 )у – 2 = 0.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1074. Складіть лінійне рівняння з двома змінними за такими даними: 1) периметр прямокутника зі сторонами а см і b см дорівнює 80 см; 2) 2 кг цукерок і 3 кг печива коштують 125 грн; 3) за 3 год до зустрічі два автобуси проїхали відстань 300 км; 4) книжка дорожча за зошит на 12 грн.
1075. Складіть задачу, подібну до попередньої, про: 1) кількість дівчат і хлопців у вашому класі; 2) покупку зошитів у лінійку і в клітинку.
ЗАДАЧІ НА ПОВТОРЕННЯ
1076. Обчисліть значення виразу 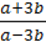 якщо:
якщо:
1) а = 4, b = -2; 2)а = -0,5, b =  .
.
1077. Знайдіть три послідовні непарні числа, сума яких дорівнює 369.