ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ
РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
&20. ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ
Ви вже знаєте, що рівняння можна поділити на види за кількістю змінних. У цьому параграфі розглядатимемо рівняння з однією змінною.
Запам’ятайте!
Рівняння виду ах + b = 0, де х – змінна, а і b – деякі числа, називається лінійним рівнянням з однією змінною.
Числа a i b називають коефіцієнтами лінійного рівняння. Число b інакше називають вільним членом даного рівняння.
? Чи можна вважати лінійним рівнянням з однією змінною рівняння виду aх =
Усі інші рівняння з однією змінною, які рівносильні рівнянню ах + b = 0, зводяться до лінійного рівняння шляхом тотожних перетворень. Наприклад, рівняння mх + nх + р = 0 можна звести до лінійного рівняння так: (m +n) х + р = 0, kx + р = 0, де k = m + n.
Залежно від того, яких значень набувають коефіцієнти а і b, лінійне рівняння з однією змінною може мати різну кількість коренів (табл. 25).
Таблиця 25
Значення а і b | Вигляд рівняння | Розв’язання | Кількість |
А ≠ 0, B ≠ 0 | Ах + b = 0 | Ах = – b, х= – | 1 корінь |
А ≠ 0, B = 0 | Aх = 0 | Х = 0 : а, х = 0 | 1 корінь |
А = 0, B ≠ 0 | 0 ∙ x + b = 0 | 0 ∙ х = – b, не існує числа, яке в добутку з числом 0 дасть число – b. Тому рівняння коренів не має | Немає коренів |
A = 0, B = 0 | 0 ∙ x = 0 | 0 ∙ x = 0, замість x можна підставити будь-яке число й отримати число 0. Тому будь-яке значення х є коренем рівняння | Безліч коренів |
Ви знаєте, що рівняння можна поділити на види й за іншою основою – залежно від степеня многочлена, який породжує дане рівняння. Якщо многочлен – першого степеня, то і відповідне рівняння є рівнянням першого степеня.
? Чи кожне лінійне рівняння з однією змінною є рівнянням першого степеня? Ні. Наприклад, лінійні рівняння 0 ∙ x + b = 0 і 0 ∙ x = 0 не є рівняннями першого степеня.
Зверніть увагу:
– лінійне рівняння з однією змінною є рівнянням першого степеня лише тоді, коли а ≠ 0;
– лінійне рівняння з однією змінною може мати або 1 корінь, або безліч коренів, або не мати коренів;
– рівняння першого степеня з однією змінною завжди має 1 корінь.
Розв’язування багатьох рівнянь з однією змінною зводиться до розв’язування лінійних рівнянь.
Задача 1. Розв’яжіть рівняння -3(х – 12) = 2х + 11.
Розв’язання. Зведемо дане рівняння до лінійного. Для цього застосуємо властивості рівносильності рівнянь і тотожні перетворення. Розкриємо дужки в лівій частині рівняння:
-3х + 36 = 2х + 11.
Перенесемо доданки в ліву частину рівняння та зведемо подібні доданки:
-3х – 2х + 36 – 11 = 0.
Отримали лінійне рівняння:
-5х + 25 = 0
Звідси -5х = -25 і х = 5.
Отже, число 5 є коренем рівняння -3(х – 12) = 2х + 11.
За допомогою рівнянь можна розв’язувати різноманітні задачі. Для цього за умовою задачі складають рівняння, розв’язавши яке, дістають відповідь. Такий спосіб розв’язування задач називають алгебраїчним. Він передбачає наступні етапи: 1) аналіз умови задачі та складання рівняння; 2) розв’язування рівняння; 3) запис відповіді.
Задача 2. Із двох пунктів, відстань між якими дорівнює 250 км, виїхали назустріч один одному два автобуси. Швидкість одного з них на 5 км/год більша за швидкість іншого. Знайдіть швидкість кожного автобуса, якщо вони зустрілися через 2 год після початку руху.
Розв’язання. Нехай х км/год – швидкість першого автобуса, тоді (х + 5) км/год – швидкість другого автобуса. Складемо короткий запис даних задачі у вигляді таблиці 26.
Таблиця 26
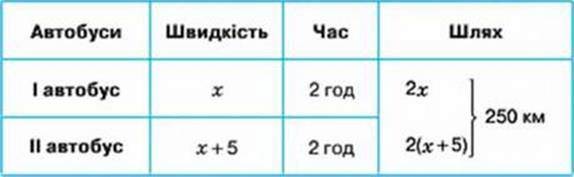
Складемо та розв’яжемо рівняння:
2х + 2(х + 5) = 250,
2х + 2х + 10 = 250,
4х = 250 – 10,
4х = 240, | : 4 х = 60.
Отже, швидкість першого автобуса дорівнює 60 км/год. Тоді швидкість другого автобуса становить х + 5 = 60 + 5 = 65 (км/год).
Дізнайтеся більше
1. Найдавніші давньоєгипетські математичні тексти відносять до початку II тис. до н. е. Математика тоді використовувалася в астрономії, мореплавстві, вимірюванні земельних ділянок, під час будівництва будинків, гребель, каналів і військових укріплень. Грошових розрахунків, як і самих грошей, у Єгипті не було. Єгиптяни писали на папірусі. Однією з історичних пам’яток, які дійшли до нас, є папірус Рінда. Це давньоєгипетський навчальний посібник з арифметики та геометрії періоду Середнього царства, переписаний (бл. 1650 до н. е.) на папірус, який зберігся дотепер, переписувачем на ім’я Ахмес. Усі завдання з папірусу Рінда мають прикладний характер і пов’язані з практикою будівництва, розмежуванням земельних ділянок тощо. Запис рівняння x ( +
+  +
+  + 1) = 37 у цьому папірусі має такий вигляд (мал. 62):
+ 1) = 37 у цьому папірусі має такий вигляд (мал. 62):

Мал. 62
2. Ім’я Мирона Онуфрійовича Зарицького (1889-1961) – талановитого математика, обдарованого педагога і популяризатора математичних знань, майже невідоме в Україні, хоча свого часу на праці українського вченого посилалися або цитували їх окремі положення французький математик Фреше, німецький математик Гільберт, професор з Варшави Серпінський та ін. Наукові інтереси М. О. Зарицького охоплюють здебільшого теорію множин з алгеброю логіки та теорію функцій дійсної змінної. Мирон Онуфрійович був великим знавцем історії математики, особливо античної, читав курси лекцій з історії математики у Львівському університеті, опублікував кілька праць з історії точних наук.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Яке рівняння називається лінійним?
2. Що таке коефіцієнти лінійного рівняння?
3. Яке число називають вільним членом лінійного рівняння?
4. Скільки коренів може мати лінійне рівняння?
5. Поясніть, як розв’язати задачу алгебраїчним методом
1017. Назвіть коефіцієнти лінійного рівняння з однією змінною:
1) 4х + 16 = 0; 3) -0,5х – 15 = 0;
2) 1у – 28 = 0; 4) – Y +
Y +  = 0.
= 0.
Яке число є вільним членом рівняння?
1018. Чи є лінійним рівнянням з однієї змінною таке рівняння:
1) 5х = 25;
2) 2у + 2 = 8;
3) 3х – 4у = 12;
4) 5у2 – 2у = 0?
Відповідь поясніть.
1019. Яке із чисел -8, -3, -2, 2, 3 чи 8 є коренем рівняння:
1) 10х + 20 = 0;
2) 4y – 12 = 0;
3) 0,3x + 2,4 = 0;
4) -3у – 9 = 0?
1020. Скільки коренів має рівняння:
1) -6х + 6 = 6;
2) 0y + 25 = 0;
3) 5х = 5х;
4) 8у + 2 = 0?
1021. Складіть лінійне рівняння з однією змінною, якщо:
1) а = 8, b = -5; 2) а = 1 , b = -0,2. Розв’яжіть отримане рівняння.
, b = -0,2. Розв’яжіть отримане рівняння.
1022. Складіть лінійне рівняння з однією змінною, якщо а = -4, b = 2,8. Розв’яжіть отримане рівняння.
1023. Знайдіть корінь рівняння:
1) 20 – 5х = 0; 4) 11 у – 0,6 = -0,6;
2) 0,4 у + 6 = 0; 5)  х + 5 = -5;
х + 5 = -5;
3) 1,8х + 9 = 9; 6) -24у – 20 = -2,25у.
1024. Знайдіть корінь рівняння:
1) 15х – 12 = 0; 3)  Х + 15 = 15;
Х + 15 = 15;
2) 20 – 0,5 у = 0; 4)  У + 2,7 = 0,4y.
У + 2,7 = 0,4y.
1025. Складіть лінійне рівняння з однією змінною, коренем якого 2 є число:
1)-4; 2) 2 .
.
1026. Складіть лінійне рівняння з однією змінною, коренем якого є число:
1)7; 2)-2,2.
1027. У двох 7-х класах навчаються 59 учнів, причому в 7-А класі на 5 учнів більше, ніж у 7-Б класі. Скільки учнів навчається в кожному класі?
1028. На двох полицях стоять 63 книжки, причому на одній із них на 9 книжок менше, ніж на іншій. Скільки книжок стоїть на кожній полиці?
1029. У трьох цехах фабрики працює 1040 робітників. У другому цеху працює на 50 робітників більше, ніж у першому, а в третьому – на 20 робітників менше, ніж у другому. Скільки робітників працює в кожному цеху?
1030. У трьох сувоях 800 м тканини. У другому сувої тканини на 20 м менше, ніж у першому, і на 15 м більше, ніж у третьому. Скільки метрів тканини в кожному сувої?
1031. Периметр прямокутника дорівнює 80 см. Знайдіть довжини його сторін, якщо одна з них утричі більша за іншу.
1032. Периметр прямокутника дорівнює 70 см. Знайдіть довжини його сторін, якщо одна з них на 5 см більша за іншу.
1033. Зведіть рівняння до лінійного та розв’яжіть його:
1) (х + 1) = 4(1 – х) +4;
2) 0,7(3у – 1,5) = 3,2(1 – 2у);
3) -2(х – 2) + (6х – 1) 2 = 10х – 14;
4) 6у – 0,5(4 – y) = 5 -1,5y;
5) 2 –  (7 – 2х) = (х – 3)
(7 – 2х) = (х – 3)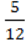 ;
;
6)  (у – 9) – 0,3(9 – у) =
(у – 9) – 0,3(9 – у) =  (2у – 3);
(2у – 3);
7) 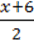 +
+ 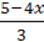 +
+ 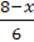 ;
;
8) 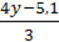 –
– 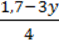 =
= 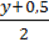 ;
;
9) (х – 1 )(х + 1) + 2(х – 3) = х2;
10) 5у(5у – 2) = (5у – 1 )(5 у + 1);
11) (у – 6)2 – у(у + 8) = 2;
12) (3z + 1)2 = 9z(z + 2) – 2.
1034. Зведіть рівняння до лінійного та розв’яжіть його:
1) 5 – 2(3 – у) = 3(1 -2у); 4) (у – 2)(у + 4) = (у + 6)2;
2) 0,4(3х – 4) = 3,2(х – 2); 5) (х – 4)2 – (х + 4)2 = 16;
3)  (
( X + 0,5) – 3 = –
X + 0,5) – 3 = – X – 1,5; 6) 3у2 + 12у -3(у + 1 )2 = 21.
X – 1,5; 6) 3у2 + 12у -3(у + 1 )2 = 21.
1035. За якого значення змінної:
1) значення виразу 4(х – 2)(х + 2) дорівнює значенню виразу (2х – 1)2 – 1;
2) значення виразу 5(у + 3)(у – 1) на 4 більше за значення виразу (3 + 2 у)2 + у2;
3) значення виразу 3(х – 1)2 на 3 менше від значення виразу (х – 6)(х + 6) + 2х2;
4) значення виразу у(у – 2) у 16 разів менше відзначення виразу (4у – 5)2 + 7?
1036. За якого знамення змінної:
1) значення виразу х(х – 3) на 12 менше від значення виразу (х – 6)(x + 2);
2) значення виразу (у – 5)2 дорівнює значенню виразу у(у -1) – 2?
1037. Два автомобілі виїхали одночасно назустріч один одному із двох пунктів А і В, відстань між якими дорівнює 455 км, і зустрілись через 3,5 год. Знайдіть швидкість кожного автомобіля, якщо швидкість одного з них на 10 км/год більша за швидкість іншого.
1038. Відстань між пунктами А і В дорівнює 310 км. Два автомобілі одночасно виїхали з цих пунктів назустріч один одному і зустрілись через 2 год. Знайдіть швидкість кожного автомобіля, якщо швидкість одного з них на 5 км/год менша від швидкості іншого.
1039. Два автобуси одночасно і в протилежних напрямках виїхали з двох містечок, відстань між якими становить 40 км. Швидкість одного автобуса на 10 км/год менша від швидкості іншого. Знайдіть швидкість кожного автобуса, якщо через 2 год відстань між ними становила 260 км.
1040. Автомобілі виїхали одночасно із пункту А в протилежних напрямках. Один автомобіль їхав зі швидкістю, на 10 км/год більшою, ніж інший. Знайдіть швидкість кожного автомобіля, якщо через 2,5 год відстань між ними становила 375 км.
1041. Мотоцикліст за 3 год проїжджає ту саму відстань, що автомобіліст за 1,5 год. Знайдіть швидкість мотоцикла і швидкість автомобіля, якщо швидкість автомобіля на 40 км/год більша, ніж швидкість мотоцикла.
1042. Велосипедист за 1,5 год проїжджає ту саму відстань, що турист проходить за 5 год. Знайдіть швидкість велосипедиста і швидкість туриста, якщо швидкість велосипедиста на 7 км/год більша, ніж швидкість туриста.
1043. Катер долає відстань між двома пристанями за течією річки за 2 год, а проти течії – за 3 год. Знайдіть відстань між цими пристанями, якщо власна швидкість катера дорівнює 15 км/год.
1044. Знайдіть відстань між двома пристанями, якщо моторний човен долає цю відстань за течією річки за 3 год, а проти течії – за 4 год. Швидкість течії річки дорівнює 5 км/год.
1045. Знайдіть чотири послідовні натуральні числа, якщо добуток перших двох із цих чисел на 18 менший від добутку двох наступних чисел.
1046. Знайдіть три послідовні натуральні числа, якщо квадрат більшого із цих чисел на 10 більший за добуток інших двох чисел.
1047. Знайдіть корені рівняння:
1) х2 + 2х = 0; 3) х3 – 4х2 – х + 4 = 0;
2) у2 + 3у – 5у – 15 = 0; 4) 5у2 + 3у2 = 20у + 12.
1048. Розв’яжіть рівняння:
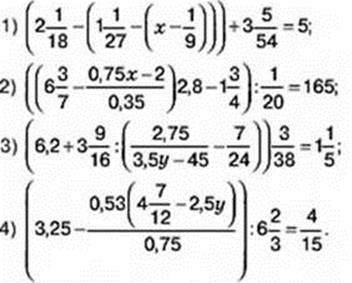
1049. Розв’яжіть рівняння, якщо а ≠ 0:
1) ах + 1 = 5 – 2х; 3) (а2 – 4)х + 2 = а;
2) (а – 1)х + 2 = а + 1; 4) a(y – b) = b (а – 2) + 2у.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1050. Мотузку завдовжки 48 м треба розрізати на 3 частини, довжини яких відносяться, як 2 : 3 : 7. Знайдіть довжину кожної частини мотузки.
1051. Садову ділянку, довжина якої у 2 рази більша за ширину, обгородили парканом завдовжки 240 м. Визначте розміри цієї ділянки.
1052. Чи можна визначити, яка з двох ділянок землі матиме більшу площу, якщо: 1) довжина першої ділянки вдвічі більша за її ширину, а довжина другої – утричі більша за її ширину; 2) обидві ділянки мають огорожу однакової довжини?
ЗАДАЧІ НА ПОВТОРЕННЯ
1053. Oбчисліть значення виразу 2b – 5(2 – 4b) + 2(6 – 9b) – 2, якщо:
1) b = 0,5; 2) b = -20.
1054. Точка С лежить на відрізку AВ, AВ = 20 см, АС – СВ = 2 см. Знайдіть довжину відрізків АС і СВ.
