Головна ⇒ 📌Довідник з математики ⇒ Логарифм числа
Логарифм числа
Математика – Алгебра
Логарифмічна функція
Логарифм числа
Логарифмом числа N за основою а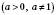 називається показник степеня x, до якого треба піднести a, щоб дістати число N.
називається показник степеня x, до якого треба піднести a, щоб дістати число N.
Позначення: 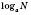 . Якщо
. Якщо 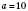 , одержуємо десятковий логарифм, який позначається
, одержуємо десятковий логарифм, який позначається 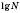 . Натуральний логарифм, тобто логарифм за основою e, позначається
. Натуральний логарифм, тобто логарифм за основою e, позначається 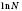 .
.
Основна логарифмічна тотожність:
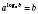
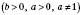 .
.
Властивості логарифмів
Для будь-яких 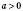 ,
, 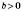 ,
, 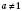 ,
, 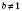 і будь-яких додатних х і у:
і будь-яких додатних х і у:
1) 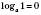 .
.
2) 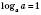 .
.
3) 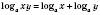 .
.
4) 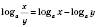 .
.
5) 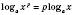 .
.
6) 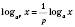 .
.
7) 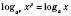 .
.
8) 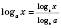 .
.
9) 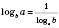 .
.
Related posts:
- Основні властивості кубічного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості кубічного кореня Для будь-яких дійсних чисел a й b: 1) а = ()3; 2) = а; 3) = ; 4) якщо b ≠ 0, то ; 5) = тільки тоді, коли а = b; 6) < тільки тоді, коли а < b; 7) < тільки тоді, […]...
- Логарифм числа. Основна логарифмічна тотожність Тема. Логарифм числа. Основна логарифмічна тотожність Мета уроку. Формування поняття логарифма числа. Познайомити учнів з основною логарифмічною тотожністю. І. Аналіз контрольної роботи II. Сприймання і усвідомлення поняття логарифма числа, основної логарифмічної тотожності Рівняння ах = b, де a > 0, а? 1, b > 0 (рис. 162) має єдиний корінь. Цей корінь називається логарифмом числа […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Основні властивості логарифмів УРОК 54 Тема. Основні властивості логарифмів Мета уроку. Вивчення основних властивостей логарифмів. Познайомити учнів з логарифмуванням і потенціюванням виразів. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправ № 4, 6, 18. 2. Усне розв’язування вправ на обчислення логарифмів з використанням таблиці 22 для усних обчислень. Таблиця 22 1 2 3 4 5 1 […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Логарифмічні функції Математика – Алгебра Логарифмічна функція Логарифмічні функції Функцію називають Логарифмічною функцією з основою a. Логарифмічна та показникова функції є взаємно оберненими. Властивості логарифмічної функції : Графіки показникової (рисунок 1) і логарифмічної (рисунок 2) функцій з однаковою основою симетричні відносно прямої . Рис. 1 Рис. 2...
- Тригонометричний запис комплексного числа – КОМПЛЕКСНІ ЧИСЛА Формули й таблиці МАТЕМАТИКА КОМПЛЕКСНІ ЧИСЛА Тригонометричний запис комплексного числа Z = r (cosα + isinα) R = – модуль комплексного числа; α – аргумент комплексного числа; Значення α, узяте в межах одного кола, -π < α < π називається головним значенням аргументу....
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- Натуральні числа і дії над ними Математика – Алгебра Натуральні числа і дії над ними Числа, які використовуються при лічбі предметів, називаються Натуральними числами. Натуральний ряд чисел є нескінченним. Він записується так: 1, 2, 3, … 0 не є натуральним числом. Зазвичай прийнято користуватись Позиційною десятковою системою числення. Тобто кожне число може бути записане за допомогою десяти цифр (0, 1, 2, […]...
- Дії з комплексними числами – КОМПЛЕКСНІ ЧИСЛА Формули й таблиці МАТЕМАТИКА КОМПЛЕКСНІ ЧИСЛА Числа виду а + ib, де а і b – будь-які дійсні числа, і – уявна одиниця, називаються комплексними. І2 = -1 – уявна одиниця. Z = a + ib. ReZ = a – дійсна частина числа Z. LmZ = ib – уявна частина числа Z. B – коефіцієнт […]...
- ВІДНІМАННЯ ДРОБУ ВІД НАТУРАЛЬНОГО ЧИСЛА Цілі: – навчальна: удосконалити вміння застосовувати правила віднімання дробу від натурального числа до розв’язування задач; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; – виховна: виховувати інтерес до вивчення математики, позитивне ставлення до навчання; Тип уроку: застосування знань і вмінь. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ ____________________________________________ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...
- Основна тригонометрична тотожність – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основна тригонометрична тотожність Для будь-якого x...
- Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Урок № 37 Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості […]...
- Перетворення звичайних дробів на десяткові – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Перетворення звичайних дробів на десяткові Щоб перетворити звичайний дріб на десятковий, треба ділити чисельник на знаменник за правилом ділення десяткових дробів. У деяких випадках отримаємо скінченний десятковий дріб. Приклад . В інших випадках дістанемо нескінченний періодичний десятковий дріб, тобто такий, у записі якого одна чи декілька цифр […]...
- Модуль числа Математика – Алгебра Раціональні числа Модуль числа Відстань від початку відліку до точки, що зображає число на координатній прямій, називається Модулем даного числа. Позначення: – модуль а. Очевидно, що для додатних чисел і 0 , для від’ємних . для будь-якого числа а. Модулі протилежних чисел рівні: . Приклади 1) ; ; . 2) Розв’яжіть рівняння. […]...
- Перетворення звичайного дробу в десятковий і навпаки Математика – Алгебра Порівняння та округлення натуральних чисел і десяткових дробів Перетворення звичайного дробу в десятковий і навпаки Будь-який десятковий дріб можна записати як звичайний із знаменником виду 10, 100, 1000 і так далі: ; ; . Щоб перетворити звичайний дріб на десятковий, треба чисельник поділити на знаменник за правилом ділення десяткових дробів. Інколи таке […]...
- Взаємно обернені числа Математика – Алгебра Множення і ділення звичайних дробів Взаємно обернені числа Два числа, добуток яких дорівнює 1, називають Взаємно оберненими. Наприклад, взаємно оберненими є числа: і ; 5 і ; 4 і 0,25; і . Число 1 є оберненим до самого себе. Число 0 не має оберненого....
- ЧИСЛО 10. ПОНЯТТЯ “ДЕСЯТИЙ”. ДОПОВНЕННЯ ДО 10. УТВОРЕННЯ ЧИСЛА 10. НАТУРАЛЬНІ ЧИСЛА ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 36. ЧИСЛО 10. ПОНЯТТЯ “ДЕСЯТИЙ”. ДОПОВНЕННЯ ДО 10. УТВОРЕННЯ ЧИСЛА 10. НАТУРАЛЬНІ ЧИСЛА Мета: ввести поняття “десятий”; ознайомити учнів з утворенням числа 10 і написанням числа за допомогою цифр 1 і 0; учити порівнювати предмети, доповнювати до 10; закріплювати вміння співвідносити […]...
- Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...
- Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193) Тема. Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193). Мета. Ознайомити учнів з правилом записування будь-якого чотирицифрового числа; закріплювати вміння учнів читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною, розв’язувати задачі двома способами. Обладнання. Нумераційна таблиця; таблиця […]...
- Дільники натурального числа. Прості і складені числа Урок № 1 Тема. Дільники Натурального Числа. Прості І Складені Числа Мета: систематизувати знання учнів про зміст дії ділення натуральних чисел; розширити знання учнів про властивості ділення натуральних чисел, доповнити їх уявленням про такі поняття, як дільник числа, кратне числу, прості і складені числа; сформувати вміння учнів знаходити дільник числа та класифікувати натуральні числа залежно […]...
- ЧИСЛО І ЦИФРА 6. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “ШОСТИЙ”. “СУСІДИ” ЧИСЛА. СКЛАД ЧИСЛА 6. НАПИСАННЯ ЦИФРИ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 23. ЧИСЛО І ЦИФРА 6. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “ШОСТИЙ”. “СУСІДИ” ЧИСЛА. СКЛАД ЧИСЛА 6. НАПИСАННЯ ЦИФРИ 6 Мета: ознайомити учнів з утворенням числа б прилічуванням та цифрою 6, з поняттям “шостий”; вчити називати “сусідів” числа, склад числа б, писати […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...
- ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 34. ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ Мета: ознайомити учнів з поняттям “одноцифрові числа”; узагальнити поняття “число” і “цифра”; учити порівнювати числа, складати приклади за числовими променями; розвивати мислення; виховувати інтерес до математики. Хід уроку […]...
- Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934) Тема. Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934). Мета. Ознайомити учнів із множенням трицифрових чисел на двоцифрові; закріплювати вміння учнів розв’язувати задачі на знаходження числа за двома різницями; удосконалювати вміння учнів розв’язувати задачі на знаходження дробу від […]...
- Квадрат і куб числа Математика – Алгебра Натуральні числа і дії над ними Квадрат і куб числа Добуток двох однакових множників записують : . Вираз читають: а у квадраті. Приклади ; ; . Добуток трьох однакових множників записують : . Вираз читають: а в кубі. Приклади ; ; ; ....
- Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь з раціональним показником N ) Для будь-якого невід’ємного числа а й натурального числа n (n ≥ 2) існує одне невід’ємне число b, при якому bn = а й позначається . Звідси випливає: 1. = 0 тільки при а = 0; 2. = 1 тільки при а = […]...
- ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...
- Логарифмічна функція, її графік і властивості УРОК 56 Тема. Логарифмічна функція, її графік і властивості Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправ № 13, 15, 20. 2. Розв’язування вправ, аналогічних домашнім. А) Обчисліть: ; . =====–=. ====–= 5. Б) Обчисліть . ==== 52 – 3-2 = 25 […]...