Основна тригонометрична тотожність – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ

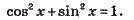
Related posts:

1. Формули перетворення добутків у суми – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення добутків у суми Для будь-яких α і β...
2. Формули перетворення сум у добутки – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення сум у добутки Для будь-яких α і β...
3. Формули подвійного і потрійного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули подвійного і потрійного аргументу Для будь-якого α Якщо Якщо...
4. Формули зниження степеня – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули зниження степеня Для будь-якого α Якщо , то Якщо α ≠ kπ, то...
5. Основні тригонометричні тотожності – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні тотожності...
6. Співвідношення між прямими й оберненими тригонометричними функціями – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між прямими й оберненими тригонометричними функціями...
7. Формули половинного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули половинного аргументу Для будь-якого α Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то Для тангенса й котангенса половинного аргументу є ще й інші формули, що не містять радикалів. Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то...
8. Формули додавання – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули додавання Для будь-яких α, β Для будь-яких α й β, якщо то А якщо то...
9. Співвідношення між тригонометричними функціями одного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між тригонометричними функціями одного аргументу Для будь-якого Для будь-якого Для будь-якого Для будь-якого Для будь-якого...
10. Основні тригонометричні рівняння – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні рівняння Sin x = 0 X = πk, k Z Cos x = 0 X = π/2 + 2πk, k Z Sin x = 1 X = π/2 + 2πk, k Z Cos x = 1 X = 2πk, k Z Sin x = -1 X […]...
11. Логарифм числа. Основна логарифмічна тотожність Тема. Логарифм числа. Основна логарифмічна тотожність Мета уроку. Формування поняття логарифма числа. Познайомити учнів з основною логарифмічною тотожністю. І. Аналіз контрольної роботи II. Сприймання і усвідомлення поняття логарифма числа, основної логарифмічної тотожності Рівняння ах = b, де a > 0, а? 1, b > 0 (рис. 162) має єдиний корінь. Цей корінь називається логарифмом числа […]...
12. Рівняння х2 = а. Основна тотожність квадратного кореня Урок № 36 Тема. Рівняння х2 = а. Основна тотожність квадратного кореня Мета: повторити та узагальнити знання учнів щодо способу розв’язання рівняння виду х2 = а (записати алгоритм розв’язання рівняння із використанням знань учнів про арифметичний квадратний корінь з невід’ємного числа); використовуючи означення арифметичного квадратного кореня з невід’ємного числа, сформулювати основну тотожність для квадратного кореня; […]...
13. Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
14. Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
15. ТОТОЖНІСТЬ РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ &4. ТОТОЖНІСТЬ Ви знаєте, що два вирази зі змінними можуть бути тотожно рівними. Наприклад, такими є пари виразів 3а – а і 2а, 3xy ∙ (- 5z)і – 15xyz, 55nm: 11 i 5nm для будь-яких значень змінних, що входять до них. Якщо в кожній із цих пар вирази поєднати знаком […]...
16. ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
17. Тотожність Розв’яжіть задачі 132. 1) Ні; 2) ні; 3) так. 133. 1) Ні; 2) ні; 3) так. 134. 1) Ні; 2) так. 135. Так. Наприклад: 12 = 12. 136. 1) Ні; 2) ні; 3) так; 4) ні; 5) так; 6) так, при а, с ≠ 0. 137. 1) Ні; 2) ні; 3) так; 4) так, 138. […]...
18. Основні властивості кубічного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості кубічного кореня Для будь-яких дійсних чисел a й b: 1) а = ()3; 2) = а; 3) = ; 4) якщо b ≠ 0, то ; 5) = тільки тоді, коли а = b; 6) < тільки тоді, коли а < b; 7) < тільки тоді, […]...
19. Визначення структурної формули – Визначення формули АНАЛІЗ ОРГАНІЧНИХ СПОЛУК 1.4 . Визначення структурної формули Для знайденої молекулярної формули спочатку записують усі можливі ізомерні структури. Далі перевіряють типові властивості цих речовин, щоб встановити, яка структурна формула підходить до визначуваної речовини. Приклад. Для молекулярної формули С2Н60 маємо дві можливі структурні формули. Етанол розчиняється у воді (водневий зв’язок), а етер не розчиняється. Етанол на […]...
20. Основні властивості арифметичного квадратного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості арифметичного квадратного кореня Для будь-яких дійсних чисел а й b: 1) якщо а ≥ 0, , то а = ()2; 2) = |a|; 3) якщо а ≥ 0 й b ≥ 0, то = ; 4) якщо а ≥ 0 й b > 0, то ; […]...
21. Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Розділ 1. ЦІЛІ ВИРАЗИ & 2. Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Знайдемо значення виразів 2(х – 1) і 2х – 2 для деяких даних значень змінної х. Результати запишемо в таблицю: Х -4 -3 -2 -1 0 1 2 3 4 2(х – 1) -10 -8 -6 -4 -2 0 2 4 […]...
22. Дії з дробами Формули й таблиці МАТЕМАТИКА Дії з дробами...
23. Формули Математика – Алгебра Натуральні числа і дії над ними Формули Якщо співвідношення між якимись змінними записане у вигляді рівності, така рівність називається Формулою. Приклади Формула периметра квадрата , де P – периметр квадрата, а – сторона ква­драта. Формула відстані , де s – відстань, v – швидкість, t – час. Формула площі прямокутника , де […]...
24. Тотожні вирази. Тотожність. Тотожні перетворення Урок № 15 Тема. Тотожні вирази. Тотожність. Тотожні перетворення Виразів Мета: систематизувати й узагальнити знання учнів про перетворення виразів, набуті учнями в 5-6 класах; поглибити знання про види виразів (тотожні вирази); оволодіти новою термінологією. Тип уроку: засвоєння знань. Хід уроку І. Перевірка домашнього завдання № 2 – зібравши зошити, перевіряємо якість виконання завдань. Розв’язання і […]...
25. Формули скороченого множення Математика – Алгебра Многочлен Формули скороченого множення – Формула різниці квадратів. Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів. – Формула квадрата суми. Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу. – Формула квадрата різниці. Квадрат різниці двох виразів дорівнює квадрату […]...
26. Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції з раціональними показниками...
27. Теорема Вієта – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Теорема Вієта Щоб числа x1 та х2 були розв’язками рівняння ах2 + bх + с = 0, необхідно й достатньо, щоб:...
28. Формули зведення УРОК 14 Тема. Формули зведення Мета уроку: вивчення формул зведення, формування умінь учнів застосовувати вивчені формули для спрощення ви­разів та обчислень. І. Перевірка домашнього завдання 1. Відповіді на питання учнів, що виникли в процесі виконан­ня домашнього завдання. 2. Самостійна робота. 1. Спростіть . (3 бали) 2. Знайдіть tg 2?, якщо tg? = – 0,4. (3 […]...
29. Основна властивість дробу – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Основна властивість дробу Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме натуральне число, дістанемо дріб, що дорівнює даному. Рівні дроби – це різні записи одного й того ж числа. Застосування основної властивості дробу Скорочення дробу Ділення чисельника і знаменника дробу на їхній […]...
30. Формули в органічній хімії ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ III. ОРГАНІЧНА ХІМІЯ 10. Теоретичні основи органічної хімії 10.3. Формули в органічній хімії В органічній хімії використовують декілька типів формул. 1. Електронні формули схематично відображують механізм утворення ковалентного хімічного зв’язку в молекулах: 2. Молекулярні формули показують якісний і кількісний склад речовини. У свою чергу, молекулярні формули […]...
31. СТРУКТУРА ТЕКСТУ: ЗАЧИН, ОСНОВНА ЧАСТИНА, КІНЦІВКА; ВІДОМЕ Й НОВЕ. ТЕМА Й ОСНОВНА ДУМКА ТЕКСТУ Мета: навчальна: повторити, поглибити, систематизувати й узагальнити знання, уміння та навички; розвивальна: розвивати вміння орієнтуватися, аналізувати та створювати тексти, дотримуючи встановленої структури; виховна: інтерес до текстів, їхньої тематики і основної думки. Внутрішньопредметні зв’язки: мова і мовлення, граматика, орфографія, пунктуація. Міжпредметні зв’язки: мови, література та інші шкільні предмети. Тип уроку: систематизація й узагальнення вивченого матеріалу. ПЕРЕБІГ […]...
32. Основна властивість дробу. Скорочення дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Основна властивість дробу. Скорочення дробів Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз, то дістанемо дріб, який тотожно дорівнює даному. Це дозволяє скорочувати дроби й приводити їх до нового знаменника. Приклади 1) . Зверніть увагу: щоб скоротити дріб, його чисельник і знаменник треба розкласти […]...
33. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...
34. Числові і буквені вирази. Формули УРОК 25 Тема. Числові і буквені вирази. Формули Мета: сформувати уявлення учнів про формули як ключ до розв’язання цілого класу задач; продовжувати формування вмінь учнів знаходити значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі. Тип уроку: засвоєння навичок та вмінь. Обладнання: таблиця-схема “Формули. Вирази”. Хід уроку І. Перевірка домашнього […]...
35. Прямокутний паралелепіпед – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Прямокутний паралелепіпед...
36. Правильна трикутна зрізана піраміда – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Правильна трикутна зрізана піраміда...
37. Правильна шестикутна призма – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Правильна шестикутна призма...
38. Тотожності УРОК № 2 Тема. Тотожності sin 2 ? + cos 2 ? = 1; sin (180°- ?) = sin?; cos (180°- ?) = – cos?; sin (90°- ?) = cos?; cos (90°- ?) = sin? Мета уроку: виведення формул sin2? + cos2? = 1; sin(180°- ?) = sin?; cos(180°- ?) = – cos?; sin(90°- ?) […]...
39. Кругове кільце – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Кругове кільце...
40. Правильна шестикутна піраміда – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Правильна шестикутна піраміда...