Основне рівняння кінетичної теорії газів
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 4 ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ГАЗІВ
4.5. Основне рівняння кінетичної теорії газів
Молекулярно-кінетична теорія дає змогу вивести всі закони ідеального газу (в тому числі й рівняння Менделєєва – Клапейрона) теоретично як висновки основного рівняння кінетичної теорії газів. Це рівняння виводиться на основі уявлень про хаотичний рух молекул.
Густина газу дуже мала, тому частина загального об’єму посудини, зайнятої молекулами, незначна порівняно з об’ємом
Характерною
Розглянемо тепер деякий газ, що складається з п молекул і міститься в посудині у вигляді куба з ребром Δl. Якщо довжина ребра Δl, то площа однієї грані куба Δs = Δl2, об’єм куба V = Δl3. Оскільки в посудині міститься n молекул газу, то середнє значення густини молекул газу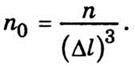 
Визначимо тиск газу на стінки посудини. В момент зіткнення молекули зі стінкою посудини вона передає їй імпульс ти, якщо удар непружний, і 2mυ у разі пружного удару. Приклад пружного удару – удар м’яча об тверду стінку, непружного – удар об стінку шматка мокрої глини. Пружний удар можна розглянути спрощено. Спочатку молекула зупиняється, причому її імпульс ти передається стінці, потім, “відштовхуючись” від стінки, знову надає їй такий самий імпульс ти. Якщо удар непружний, то весь процес удару закінчується першою стадією, молекула не відскакує від стінки, як м’яч, а прилипає до неї, як шматок глини. Зіткнення молекул газу зі стінками посудини вважатимемо пружними. Запишемо другий закон Ньютона для випадку пружного зіткнення молекули зі стінкою посудини:
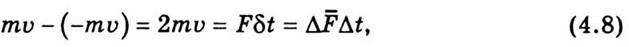
Де 2mυ – зміна імпульсу молекули; Fδt – імпульс сили, що визначається добутком сили, яка діє в момент зіткнення, на час зіткнення. Величину Fδt можна прирівняти до імпульсу сили Δ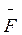
Δt, де Δ 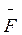– середнє значення сили на проміжок часу Δt, поки молекула пройде відстань між стінками посудини туди й назад 2Δl. Отже,
Підставимо значення Δt і у рівність (4.8):
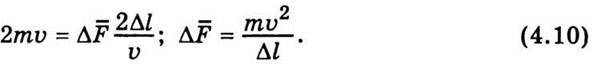
Якщо молекули рухаються в напрямі до стінки зі швидкостями υ1, υ2,…,υn’ і мають масу m, то загальну силу, з якою вони діють на стінку куба, можна записати у такому вигляді:
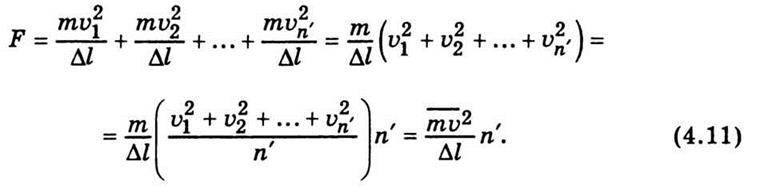
Величина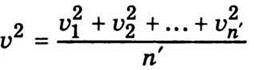 
Є середнім значенням квадратів швидкостей. Підставивши значення n’ = 
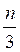та поділивши ліву й праву частини виразу (4.11) на площу Δl2 (саме на неї діє сила F), дістанемо вираз для тиску
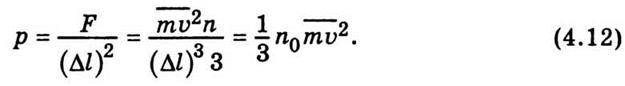
Це і є вираз для тиску, який створюють молекули газу на стінку посудини. Помноживши та поділивши праву частину рівності (4.12) на 2, дістанемо зв’язок між тиском та середньою кінетичною енергією поступального руху молекули газу:
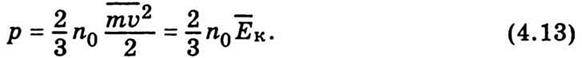
Отже, відповідно до (4.13) тиск газу дорівнює двом третинам кінетичної енергії поступального руху молекул, що містяться в одиниці об’єму. Рівняння (4.13) є основним у кінетичній теорії газів. Помножимо ліву і праву частини рівності (4.13) на об’єм моля V0. Тоді
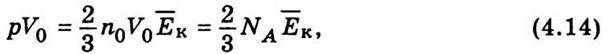
Де NА – число Авогадро. Виходячи з рівняння Менделєєва – Клапейрона (4.6), у виразі (4.14) зробимо заміну рV0 = RT. Отже,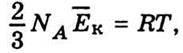 
звідси можна визначити середню кінетичну енергію молекули:
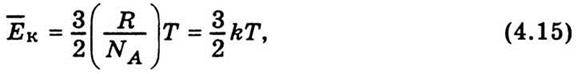
K – стала Больцмана:
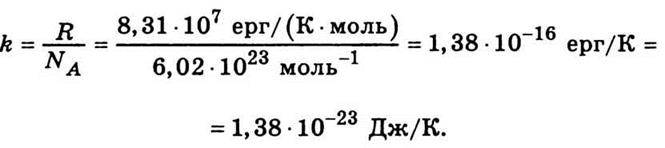
При одержанні рівняння (4.15) було враховано лише поступальні ступені вільності. Якщо врахувати обертальні та коливальні ступені вільності, то вираз для середньої кінетичної енергії молекули набирає такого вигляду:
Де і – загальне число ступенів вільності.
Ступені вільності – це незалежні (вільні) переміщення тіла в просторі, або незалежні координати, що визначають положення тіла в просторі. Число ступенів вільності для молекул одноатомного газу дорівнює 3 – це поступальні ступені вільності, які враховано у формулі (4.15). Для багатоатомних молекул слід ураховувати також обертальні ступені вільності. Тому для жорстких двохатомних молекул і = 5, для багатоатомних і = 6. Із (4.16) випливає, що середня кінетична енергія молекули прямо пропорційна абсолютній температурі.
(1 votes, average: 5.00 out of 5)
Loading...