Основні властивості числових нерівностей
УРОК № 4
Тема. Основні властивості числових нерівностей
Мета уроку: домогтися засвоєння учнями змісту поняття “оцінити значення виразу”; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв’язування вправ на порівняння буквених виразів та на доведення відповідних нерівностей, а також виробити вміння оцінювати
Тип уроку: доповнення знань, вироблення вмінь, відпрацювання навичок.
Наочність та обладнання: опорний конспект № 4.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Учні перевіряють правильність розв’язування вправ домашнього завдання самі у себе за зразком.
Сильні учні під час перевірки виконують індивідуальні завдання.
III. Формулювання мети і завдань уроку.
Мотивація
Для усвідомлення учнями необхідності вивчення основного питання уроку (використання властивостей числових нерівностей для оцінки значення виразу) можна виконати відповідне завдання практичного змісту, яке вимагало б від учнів дій, пов’язаних з оцінюванням значення виразу з використанням даної подвійної нерівності та властивостей числових нерівностей. Аналізуючи зміст та можливі шляхи розв’язання цього завдання, учні мають прийти до висновку про існування певного виду практичних завдань, виконання яких вимагає від них умінь застосовувати властивості числових нерівностей. Таким чином формулюється мета уроку: сформувати уявлення про вид завдань (на оцінювання значення виразу) та загальну схему дій при їх розв’язуванні.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. Порівняйте числа а і b, якщо:
1) a – b = -3;
2) а – b = 3,5;
3) а – b = 0.
2. Відомо, що m > n. Визначте, чи є правильним твердження:
1) числа m і n на числовій прямій розміщені так, як показано на рисунку:
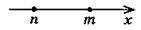
2) m > 0 і n < 0;
3) n < m;
4) 3 + m > 3 + n;
5) 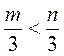 ;
;
6) 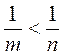 .
.
3. Нехай а – довжина сторони квадрата. Який зміст має вираз:
1) 4а; 2) а2; 3) а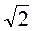 ?
?
V. Формування знань
План вивчення нового матеріалу
1. Зміст поняття “оцінити значення виразу”.
2. Послідовність дій при виконанні завдання на оцінювання значення виразу. Приклад розв’язання.
Опорний конспект № 4
Якщо точне значення величини х не відоме, але можна визначити, між якими числами а і b це значення міститься на числовій прямій (тобто a < х < Ь ), то кажуть, що значення величини оцінено х. |
Приклад. Відомо, що -1 < х < 3. Оцінимо значення виразу 2x – 5. |
Розв’язання |
Встановимо послідовність дій у виразі 2х – 5: спочатку х помножимо на 2, а потім додамо до цього виразу -5: х |
Помножимо всі частини одержаної нерівності -1 < х < 3 на 2 > 0, при цьому знак нерівності не зміниться: -2 < 2х < 6. |
Додамо до всіх частин нерівності число -5, при цьому знак нерівності не зміниться: -7 < 2х – 5 < 1. |
Методичний коментар
При формуванні уявлення учнів про зміст поняття “оцінити значення виразу” вчитель має нагадати їм про те, що на відміну від абстрактних ситуацій, що розглядаються в математичних задачах, у реальному житті ми в основному маємо справи не з точними значеннями величин (які ми можемо отримати при виконанні обчислень), а з наближеними значеннями величин (які ми можемо отримати в результаті вимірювань). Саме тому при розв’язуванні практичних задач краще ставити питання не про обчислення значення виразів, а про оцінювання значення виразів, тобто про визначення границь (чисел), за які не виходитиме наближене значення певної величини. Таким чином формулюється уявлення учнів про зміст поняття “оцінити значення виразу” і його відмінність від змісту завдання “знайти значення виразу”.
Для кращого засвоєння учнями послідовності дій при розв’язуванні відповідного завдання на оцінювання значення виразу перед вивченням матеріалу уроку на етапі актуалізації опорних знань та вмінь учнів бажано розв’язати усні вправи на повторення змісту властивостей числових нерівностей та способів міркувань при їх застосуванні для порівняння виразів і доведення нерівностей (див. вище).
VI. Формування вмінь
Усні вправи
1. Відомо, що 4 < а < 6. Оцініть значення виразу:
1) 2а; 2) 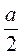 ; 3) a + 1; 4) а – 2; 5) 2а – 1; 6) – а.
; 3) a + 1; 4) а – 2; 5) 2а – 1; 6) – а.
2. Відомо, що а > b. Яка з нерівностей є правильною:
1) -3а > -3b;
2) -3 + а > -3 + b;
3) 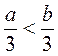 ;
;
4) а + 2 > b + 3?
Письмові вправи
Для реалізації дидактичної мети уроку учні мають розв’язати вправи такого змісту:
1) оцінити значення виразу, що містить дану змінну, якщо за умовою дано подвійну нерівність для оцінювання значення даної змінної;
2) довести нерівність із використанням властивостей числових нерівностей;
3) порівняти значення виразів, використовуючи властивості числових нерівностей.
Методичний коментар
Властивості числових нерівностей становлять ту базу, на якій надалі буде грунтуватися розв’язування лінійних та нелінійних нерівностей з однією змінною. Тому на даному уроці паралельно з виробленням умінь використовувати властивості числових нерівностей для оцінювання значення виразу продовжується робота із закріплення знань про зміст властивостей числових нерівностей та вмінь щодо способів застосування цих властивостей для порівняння значень виразів і доведення числових нерівностей.
VII. Підсумки уроку
Учні виконують завдання, аналогічні завданням тестів 1, 3, 4 експрес-контролю [9].
VIII. Домашнє завдання
1. За опорним конспектом № 4 вивчити зміст основних понять уроку.
2. Виконати вправи, що передбачають: застосування властивостей числових нерівностей для порівняння значень виразів, доведення нерівностей та оцінювання значення виразу.
3. На повторення: властивості числових рівностей та їх застосування (на прикладі розв’язування системи лінійних рівнянь з однією змінною).
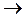 2 • х
2 • х