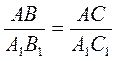Означення подібних трикутників
Урок № 26
Тема. Означення подібних трикутників
Мета: сформувати в учнів уявлення про подібні трикутники; працювати над засвоєнням учнями означення подібних трикутників, змісту поняття коефіцієнта подібності. Сформувати вміння:
– відтворювати зміст вивчених тверджень;
– виконувати записи цих тверджень математичною мовою за допомогою символу ” ~ “;
– використовувати виконані записи для обчислення невідомих елементів подібних трикутників.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Цей етап уроку проводимо у формі перевірки домашнього завдання за зразком або пропонуємо учням виконати тестове завдання.
Тестове завдання
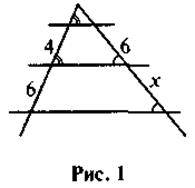
1. За даними рисунка 1 знайдіть х.
а) 4; б) 8; в) 9; г) 12.
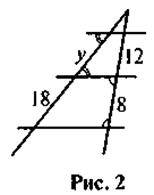
2. За даними рисунка 2 знайдіть у.
а) 27; б) 24; в) 30; г) 16.
III. Формулювання мети і завдань уроку
Для розуміння учнями вивчення матеріалу уроку пропонуємо розглянути рис. 3 та дати відповіді на такі запитання:
1) Які геометричні фігури (крім
2) Чи є трикутники АВВ1 і ACC1 рівними? Які елементи цих трикутників відповідно рівні? Чому ви так вважаєте?
3) Що можна сказати про відповідні сторони АВ і АС та АВ1 і АС1 цих трикутників?
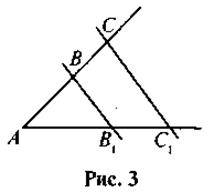
Здобуті відповіді дають учням можливість усвідомити, що узагальнена теорема Фалеса приводить до появи іншого, ніж рівність, виду відношень між фігурами (нового для учнів). Вчителю залишається сформулювати мету уроку як необхідність вивчення означення цього нового виду відношень між геометричними фігурами на прикладі найпростішого многокутника, а також дослідження властивості цього відношення та оволодіння способами його застосування під час розв’язування задач.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями означення, а також доведення властивостей подібних трикутників, учням слід активізувати знання і вміння щодо понять “рівні трикутники”, “відповідні елементи трикутників”, “периметр трикутника”, пригадати властивості кутів трикутника.
Для цього пропонуємо учням виконати усні вправи.
Виконання усних вправ
1. Відомо, що? МАС = ?BDF. Запишіть рівності, що з цього випливають: МС = …; BD = …; АС = …;  MCA = …;
MCA = …;  BDF = …;
BDF = …;  CMA = …
CMA = …
2. Яким – гострокутним, прямокутним чи тупокутним – є трикутник, якщо:
А) один із його кутів дорівнює сумі двох інших;
Б) один із його кутів більший від суми двох інших;
В) один із його кутів менший від суми двох інших?
V. Засвоєння знань
План вивчення нового матеріалу
1. Уявлення про подібні фігури.
2. Означення подібних трикутників.
3. Властивості відповідних елементів подібних трикутників.
@ Донедавна поняття подібності фігур уводилось після вивчення перетворення подібності, і тому подібні фігури визначали як такі, що переводяться одна в іншу перетворенням подібності. У чинній програмі з математики для дванадцятирічної школи порівняно з програмою 11-річної школи суттєво змінився порядок вивчення деяких розділів. Це стосується і розділу “Подібність фігур”. З огляду на це, поняття подібності фігур у новому підручнику не визначається (формується уявлення про подібні фігури на інтуїтивному рівні), а одразу формулюється означення подібних трикутників (раніше розглядалось як наслідок того, що для подібних трикутників виконуються властивості перетворення подібності).
Після формулювання математичною мовою означення подібних трикутників корисно записати, як виражаються сторони одного з подібних трикутників через коефіцієнт подібності та сторону іншого трикутника (тобто якщо в подібних трикутниках ABC і А1В1С1 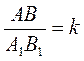 , то АВ = k • А1В1), а також сформулювати властивість, що випливає з рівності трьох відношень відповідних сторін подібних трикутників: якщо
, то АВ = k • А1В1), а також сформулювати властивість, що випливає з рівності трьох відношень відповідних сторін подібних трикутників: якщо 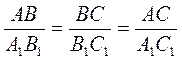 , то АВ : ВС : АС = А1В1 : В1С1 : А1С1.
, то АВ : ВС : АС = А1В1 : В1С1 : А1С1.
Також у новому підручнику порівняно з традиційним підручником геометрії приділяється набагато більше уваги властивостям подібних трикутників: вони сформульовані у вигляді опорної задачі та твердження, що міститься в теоретичній частині (див. с. 106). До властивостей, сформульованих у підручнику, автор запропонував би додати властивість радіусів вписаного в трикутник та описаного навколо трикутника кіл (див. конспект 11). Властивості відповідних лінійних елементів подібних трикутників можна запропонувати для доведення на уроці або як додаткове домашнє завдання для “сильних” учнів.
Конспект 11 | |
Подібність трикутників Означення. Два трикутники називаються подібними, якщо кут и одного з них відповідно дорівнюють кутам іншого, а відповідні сторони цих трикутників пропорційні. |
|
| |
K – коефіцієнт подібності. | |
Властивості подібних трикутників | |
1. Якщо? АВС ~ ?А1В1С1 і 2. Якщо? АВС ~ ?A1B1C1 і k – коефіцієнт подібності, то
| |
Ознаки подібності трикутників | |
Якщо в? АВС і? A1B1C1: | |
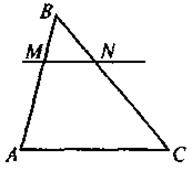
1) 2) 3) Наслідок. Якщо у? АВС: MN || AC (MN перетинає АВ і ВС), то? АВС ~ ?MВN. |
|
VI. Формування первинних умінь
Виконання усних вправ
1. Відомо, що? АВС ~ ?KMN. Назвіть відповідно рівні кути цих трикутників.
2. Трикутник ABC і трикутник з вершинами D, Е, F подібні, причому 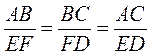 . Закінчіть запис? АВС ~ ?…
. Закінчіть запис? АВС ~ ?…
3. Чи можуть бути подібними прямокутний і тупокутний трикутники?
4. Два трикутники подібні з коефіцієнтом 0,25. У скільки разів сторони одного трикутника більші за відповідні сторони іншого?
Виконання письмових вправ
1. На рисунку 4 ?АВС ~ ?А1В1С1. За даними рисунка знайдіть х і у.
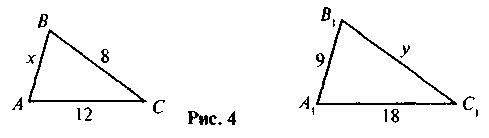
2. Відомо, що? АВС ~ ?DEF. Знайдіть кут С, якщо  A = 45°,
A = 45°,  Е = 110°.
Е = 110°.
3. Відомо, то? АВС ~ ?DEF, причому  D = 70°,
D = 70°,  B = 55°. Доведіть, що АВ = АС.
B = 55°. Доведіть, що АВ = АС.
4*. Відомо, що? АВС ~ ?KMN, причому  A +
A +  M = 90°. Доведіть, що АВ – найбільша сторона трикутника ABC.
M = 90°. Доведіть, що АВ – найбільша сторона трикутника ABC.
5 (додатково). Кут при основі рівнобедреного трикутника дорівнює 70°. На продовженні основи взяли точку і з’єднали її з вершиною даного трикутника. Виявилось, що? ADB подібний до даного трикутника (рис. 5). Знайдіть кути трикутника CBD.
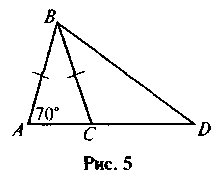
VII. Підсумки уроку
Два трикутники подібні. Чи відповідають цьому твердженню наведені умови?
1. Два кути одного трикутника дорівнюють 40° і 60°, а в іншому із трикутників є кут 80°.
2. Сторони одного із трикутників дорівнюють 1 м, 1,5 м, 2 м, а сторони іншого з трикутників дорівнюють 10 м, 15 м, 20 м.
VIII. Домашнє завдання
Вивчити означення подібних трикутників та властивості подібних трикутників (з доведенням). Розв’язати задачі.
1. На рисунку 6 ?АВС ~ ?А1В1С1. Заданими рисунка знайдіть х і у.

2. Відомо, що? АВС ~ ?DEF. Знайдіть кут F, якщо  B = 80°,
B = 80°,  A =
A =  C.
C.
3. Сторони трикутника дорівнюють 2,5 см, 4 см і 5 см. Знайдіть сторони трикутника, подібного даному, якщо його найменша сторона дорівнює найбільшій стороні даного трикутника.
4. (додатково). Периметр одного трикутника дорівнює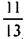 периметра іншого, подібного до нього трикутника. Різниця відповідних сторін цих трикутників дорівнює 1 м. Знайдіть ці сторони.
периметра іншого, подібного до нього трикутника. Різниця відповідних сторін цих трикутників дорівнює 1 м. Знайдіть ці сторони.
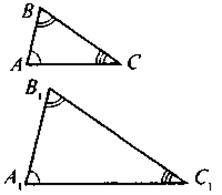
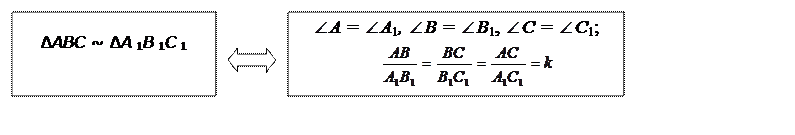

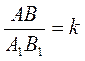 , то
, то 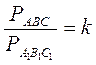
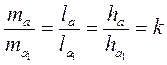
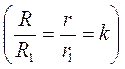
 ?АВС ~ ?A1B1C1: або
?АВС ~ ?A1B1C1: або