Переміщення та його властивості. Рівні фігури
УРОК № 33
Тема. Переміщення та його властивості. Рівні фігури
Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13].
Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення і властивості до розв’язування задач.
Хід уроку
І. Перевірка домашнього
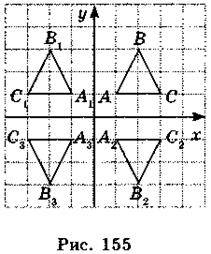
1. Правильність виконання домашнього завдання перевірити за записами, зробленими на дошці до початку уроку (рис. 155). 2. Фронтальна бесіда 1) Поясніть, що таке перетворення фігури F на фігуру F1. 2) Наведіть приклади перетворення фігур.
II. Поетапне сприймання й усвідомлення нового матеріалу
Поняття переміщення та рівних фігур
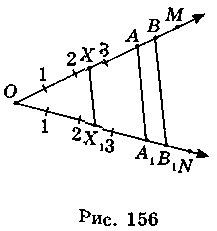
Розглянемо два відрізки ОМ і ON, які мають однакову довжину (рис. 156). Задамо перетворення відрізка ОМ на відрізок ON. Для цього на прямих ОМ і ON введемо координати, вибравши однакові одиничні відрізки і спільний початок
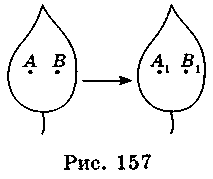
Перетворення однієї фігури на іншу називають переміщенням або рухом, якщо воно зберігає відстань між точками, тобто переводить будь-які дві точки А і В першої фігури у точки А1 і В1 другої фігури так, що АВ = А1В1 (рис. 157).
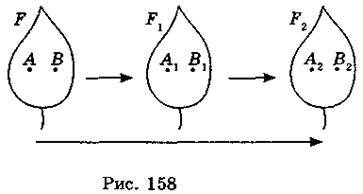
Два переміщення, виконані послідовно, дають знову переміщення (рис. 158). Якщо фігура F переводиться переміщенням у фігуру F1, а фігура F1 переводиться переміщенням у фігуру F2, то перетворення фігури F на фігуру F2 також є переміщенням.
Якщо перетворення переводить фігуру F у фігуру F1, то існує перетворення, яке переводить фігуру F1 у фігуру F, яке називається оберненим до даного. Перетворення, обернене до переміщення, також є переміщенням.
Дві фігури називаються рівними, якщо вони переводяться переміщенням одна в одну.
Доведемо теорему: при переміщенні точки, які лежать на прямій, переходять у точки, які лежать на прямій, і порядок їх взаємного розміщення зберігається.
Доведення
Нехай на прямій АВ точка С (рис. 159) лежить між точками А і В, а точки A1, B1, C1 – образи точок А, В, С, отримані в результаті переміщення. Доведемо, що точка С1 лежить на прямій A1B1 між точками А1 і В1.
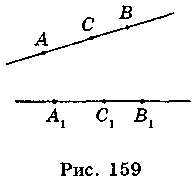
Якщо точка С лежить між точками А і В, то АВ = АС + СВ. За означенням переміщення АВ = А1В1, АС = A1С1, СВ = С1В1, отже, А1В1 = A1С1 + C1B1, а це означає, що точка С1 лежить між точками A1 і В1, тобто точки А1? В1, С1 лежать на одній прямій.
Властивості переміщення
Із останньої теореми випливає, що при переміщенні:
А) прямі переходять у прямі;
Б) промені – у промені;
В) відрізок – у відрізок;
Г) зберігаються кути між променями;
Д) півплощина переходить у півплощину.
Розв’язування вправ
1. Дано два відрізки АВ = 3 см і CD = 3,1 см. Чи існує переміщення, яке відображає відрізок АВ на CD? Чому? 2. Трикутник ABC рівносторонній. Чи існує переміщення, яке відображає:
А) відрізок АВ на ВС; б) кут В на кут С?
3. Доведіть, що при переміщенні кути між променями зберігаються.
III. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Доведіть, що при переміщенні подібні трикутники переходять у подібні трикутники. 2. Доведіть, що внаслідок переміщення паралельні прямі переходять у паралельні прямі.
IV. Домашнє завдання
1. Вивчити означення і властивості переміщення. 2. Розв’язати задачу.
Довести, що при переміщенні паралелограм переходить у паралелограм.
V. Підбиття підсумків уроку
Запитання до учнів
1. Дайте означення переміщення. 2. Назвіть властивості переміщення. 3. Який зв’язок переміщення має з рівністю фігур?