Головна ⇒ 📌Довідник з математики ⇒ Перетворення графіків функцій – Функції та графіки
Перетворення графіків функцій – Функції та графіки
Математика – Алгебра
Функції та графіки
Перетворення графіків функцій
1. Графіки функцій 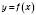 і
і 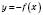 є симетричними відносно осі Ox.
є симетричними відносно осі Ox.
2. Щоб побудувати графік функції 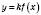
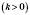 , треба графік функції
, треба графік функції 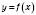 розтягнути від осі Ox в k разів, якщо
розтягнути від осі Ox в k разів, якщо 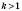 , або стиснути його в k разів до осі Ox, якщо
, або стиснути його в k разів до осі Ox, якщо 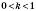 .
.
3. Щоб побудувати графік функції 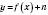 , треба
, треба
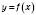 перенести на n одиниць в напрямі осі Oy, якщо
перенести на n одиниць в напрямі осі Oy, якщо 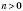 , або в протилежному напрямі, якщо
, або в протилежному напрямі, якщо 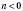 .
.4. Щоб побудувати графік функції
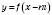 , треба графік функції
, треба графік функції 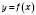 перенести на m одиниць у напрямі осі Ox, якщо
перенести на m одиниць у напрямі осі Ox, якщо 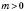 , або в протилежному напрямі, якщо
, або в протилежному напрямі, якщо 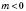 .
.На рисунках, поданих нижче, наведені приклади перетворення графіків.
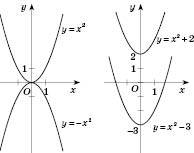
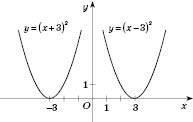
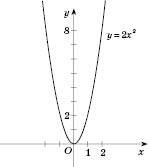
5. Щоб
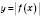 ,
,треба з’ясувати, що
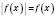 , коли
, коли 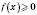 , а
, а 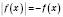 , коли
, коли 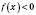 .
.Тобто ту частину графіка функції
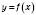 (рисунок нижче зліва), де
(рисунок нижче зліва), де 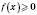 , треба залишити без змін, а ту частину, де
, треба залишити без змін, а ту частину, де 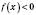 ,- замінити на симетричну відносно осі Ox (рисунок справа).
,- замінити на симетричну відносно осі Ox (рисунок справа).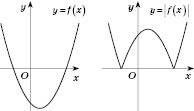
6. Щоб побудувати графік функції
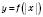 , треба ту частину графіка функції
, треба ту частину графіка функції 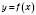 (рисунок 1), де
(рисунок 1), де 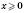 , залишити без змін і відобразити її симетрично відносно осі Oy. Ту частину графіка
, залишити без змін і відобразити її симетрично відносно осі Oy. Ту частину графіка 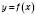 , де
, де 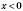 , треба відкинути (рисунок 2).
, треба відкинути (рисунок 2).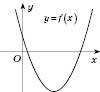
Рис. 1
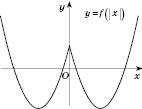
Рис. 2
Related posts:
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій УРОК 3 Тема. Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій Мета уроку: Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = […]...
- Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
- Квадратична функція – Функції та графіки Математика – Алгебра Функції та графіки Квадратична функція Квадратним тричленом називається многочлен виду , де x – змінна, a, b і c – деякі числа, причому . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння . Теорема. Якщо і – корені […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...
- Парність функції Математика – Алгебра Числові функції Парність функції Функція називається Парною, якщо: 1) ; 2) . У парних функцій протилежним значенням аргументу відповідають рівні значення функції. Графік парної функції симетричний відносно осі Oy. Функція називається Непарною, якщо: 1) ; 2) . У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції. Графік непарної функції симетричний відносно […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції УРОК № 19 Тема. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії […]...
- Функції та графіки Математика – Алгебра Функції та графіки Функція може задаватися описом, таблицею, графіком, формулою тощо. Область визначення функції зручно записувати за допомогою числових проміжків. Приклади 1) ; ; 2) ; ; 3) ; ; 4) ; . Пояснимо, як ми знайшли область визначення в останньому прикладі. Функція визначена для тих і тільки тих значень x, які […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Квадратичні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Квадратичні функції Графіком квадратичної функції є парабола, яка отримується з графіка функції у = ах2 за допомогою двох паралельних перенесень: – перенесення уздовж осі ОХ на m одиниць ліворуч, якщо m < 0, і праворуч, якщо m > 0; – перенесення уздовж осі OY на у0 одиниць […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Логарифмічні функції Математика – Алгебра Логарифмічна функція Логарифмічні функції Функцію називають Логарифмічною функцією з основою a. Логарифмічна та показникова функції є взаємно оберненими. Властивості логарифмічної функції : Графіки показникової (рисунок 1) і логарифмічної (рисунок 2) функцій з однаковою основою симетричні відносно прямої . Рис. 1 Рис. 2...
- Графіки залежності кінематичних величин від часу в разі рівномірного прямолінійного руху 1-й семестр МЕХАНІКА 1. Кінематика Урок 5/7 Тема. Графіки залежності кінематичних величин від часу в разі рівномірного прямолінійного руху Мета уроку: ознайомити учнів з графічною інтерпретацією рівномірного прямолінійного руху Тип уроку: вивчення нового матеріалу План уроку Контроль знань 5 хв. 1. Прямолінійний рівномірний рух. 2. Відносність механічного руху. 3. Закон додавання швидкостей. 4. Правило додавання […]...
- Функції Урок № 68 Тема. Функції Мета: виявити рівень засвоєння обов’язкових знань та вмінь з теми “Функція”, передбачених програмою з математики та ступінь сформованості навичок. Тип уроку: контроль знань та вмінь. Форма проведення: тематична контрольна робота. Хід уроку І. Перевірка домашнього завдання II. Умова тематичної контрольної роботи Варіант 1 Варіант 2 1?. Функцію задано формулою У […]...
- РІВНЯННЯ РУХУ. ГРАФІКИ РІВНОМІРНОГО ПРЯМОЛІНІЙНОГО РУХУ Роздiл 2 МЕХАНІЧНИЙ РУХ &18. РІВНЯННЯ РУХУ. ГРАФІКИ РІВНОМІРНОГО ПРЯМОЛІНІЙНОГО РУХУ Рівномірний прямолінійний рух тіла дуже зручно представляти і вивчати у вигляді графіків залежності шляху, пройденого тілом, від часу його руху (графік руху) і залежності швидкості тіла від часу його руху (графік швидкості). Розглянемо приклад. Нехай автомобіль рухається з Києва до Одеси зі швидкістю 100 […]...
- ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ Розділ ІІ Механічний рух & 14. ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ Визначення шляху на графіку швидкості У фізиці й математиці використовують три способи подання інформації про зв’язок між різними величинами: а) у вигляді формули, наприклад, s =v ∙ t; б) у вигляді таблиці; в) у вигляді графіка (малюнка). Залежність швидкості від часу v(t) – графік швидкості, […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Графік функції Урок № 63 Тема. Графік функції Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”. Хід уроку I. Організаційний момент Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці. II. Перевірка домашнього […]...
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних тригонометричних функцій і формул перетворення добутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...
- Таємнича мова графіки Художній образ у графіці, живописі та скульптурі 2. Таємнича мова графіки Графіка – найпоширеніший вид образотворчого мистецтва. Мова графіки лаконічна. Художник-графік передає свої думки й почуття за допомогою точок, ліній, штрихів і плям. Г. Нарбут. Українська абетка Л. Леві-Дюрмер. Автопортрет А. Даур. Г. К. Андерсен Л. Ільїна Щастя О. Козакова. Чарівна троянда (фрагмент) П. Пікассо. […]...