Перетворення Лоренца
ФІЗИКА
Частина 4
ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ
Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ
14.5. Перетворення Лоренца
Розвиваючи свою гіпотезу, X. Лоренц показав, що для подолання суперечностей, які виникли при поясненні досліду Майкельсона та інших, треба ввести нові рівняння для перетворення координат при переході від системи координат, що перебуває в стані спокою, до системи координат, яка рухається рівномірно і прямолінійно відносно першої. До цього фізики користувались перетвореннями
Розглянемо дві системи відліку К і К’ (рис. 14.5), просторові координати яких є прямокутними, декартовими. Позначимо їх відповідно через х, у, z і х’ у’, z’. Нехай система відліку К’ рухається відносно системи К прямолінійно і рівномірно вздовж координати х зі швидкістю υ. Координатні осі х і х’ збігаються за напрямом, осі у, z і у’, z’ відповідно паралельні. У момент часу t = t’ = 0 початок координат
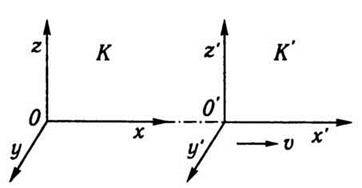
Рис. 14.5
Виявляється, що за цих умов координати тієї самої події в обох системах пов’язані такими формулами:
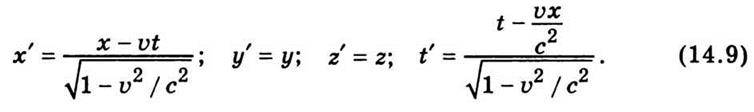
Ці формули дають змогу визначити координати х’, у’, z’, t’ деякої події в системі К’, якщо відомі її координати в системі К. Зворотний перехід від системи К до системи К’ визначають такими формулами:
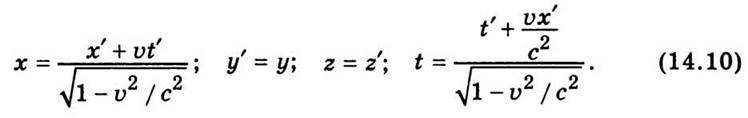
Формули (14.9) і (14.10) називають перетвореннями Лоренца, оскільки їх вперше вивів X. Лоренц. До речі, відомі рівняння Максвелла, не інваріантні перетворенням Галілея, виявилися інваріантними перетворенням Лоренца. Розглядаючи ці формули, насамперед помічаємо, що координати у, z не змінюються; це відповідає відсутності поперечного лоренцового скорочення. Формули перетворень симетричні, лише швидкість υ замінена на -υ. Це, звичайно, відповідає рівноправності всіх систем відліку. Основним є те, що змінюється не лише просторова координата х, а й час t. Це свідчить про відносність не тільки просторових координат, а й часу. Як зазначалося в ньютонівській механіці, час не змінювався при переході від однієї системи координат до іншої: t = t’. Неважко помітити, що коли швидкість и відносного руху систем відліку мала порівняно зі швидкістю світла с, перетворення Лоренца переходять у перетворення Галілея. Це означає, що релятивістська механіка не відкидає класичну, яка є граничним випадком релятивістської механіки, коли υ ” с.