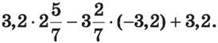Подібні доданки та їх зведення
Розділ 4 Раціональні числа і дії мідними
§46. Подібні доданки та їх зведення
Розподільна властивість множення дає можливість виносити спільний множник за дужки.
Приклад 1. Спрости вираз 7x – 6x + 3x.
Розв’язання. Усі доданки мають спільний множник х. Маємо: 7x – 6x + 3x = (7 – 6 + 3) ∙ х. У дужках записано суму коефіцієнтів усіх доданків, вона дорівнює 4.
Тому 7x – 6x + 3x = 4x.
У виразі 7x – 6x + 3x доданки 7x, -6x, 3x мають спільну буквену частину і відрізняються один від одного лише коефіцієнтами. Такі доданки називають подібними.
–
Додавання подібних доданків називають зведенням подібних доданків.
– Щоб звести подібні доданки, достатньо додати їх коефіцієнти і знайдений результат помножити на спільну буквену частину.
Приклад 2. Звести подібні доданки: 1) 4а + а – 6а; 2) 7b – 3b – 4b.
Розв’язання. 1)У цьому прикладі всі доданки подібні, оскільки в них спільна частина а. Додаючи коефіцієнти, маємо: 4 + 1 – 6 = -1. Отже, 4а + а – 6а = -1 ∙ а = – а; 2) 7b – 3b – 4b = 0 ∙ b = 0.
Вираз може містити доданки з різними буквеними частинами. Тоді доданки можна об’єднати
Приклад 3. Спростити вираз 4а + 5b – 7а + 4 + 3b.
Розв’язання.
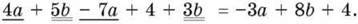
Приклад 4. Розв’язати рівняння 4(x + 2) – (x – 2) = 13. Розв’язання. Розкриємо дужки: 4x + 8 – x + 2 = 13. Зведемо подібні доданки 3x + 10 = 13. Далі 3x = 13 – 10; 3x = 3; x = 3 : 3; x = 1.
Які доданки називають подібними? Як звести подібні доданки?
1248. Назви подібні доданки у виразі:
1) 3а + 2а – 4; 2) 7b + 9 – 9b; 3) 3x + у – у.
1249. Перепиши та підкресли подібні доданки:
1) 7m + 2m – 5; 2) 4p – 3 – 2р; 3) 7t + 9k – 7t.
1250. (Усно) Зведи подібні доданки:
1) 7x – 3x; 2) 9b + 7b; 3) 9у – 9у; 4) -5m + 4m.
1251. Зведи подібні доданки:
1) 5x + 4x; 2) 3у – у; 3) 7m + m; 4) 4b + b – 2b;
5) -2a – 3a; 6) 2p + 2p; 7) -2n + n; 8) 7m – 2m – 5m.
1252. Зведи подібні доданки:
1) 7у + 3у; 2) 5m – m; 3) 2t + t; 4) 7у + у – 6у;
5) -3p – 5p; 6) 3b + 3b; 7) -3a + a; 8) 4x – x – 3x.
1253. (Усно) Спрости вираз та знайди його значення:
1) -2x – 8x, якщо x = 1,3; 2) 4m – 5m, якщо m = -2. 1254. Спрости вираз та обчисли його значення:
1) 4x – 2x, якщо x = -2,7; 2) -6m + 9m, якщо m = -4;
3) -8у – 6у, якщо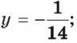 
4) 9p – 8p, якщо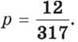 
1255. Спрости вираз та знайди його значення:
1) 9а – 6а, якщо а = -3,4; 2) -7p – 9p, якщо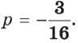 
1256. (Усно) Зведи подібні доданки:
1) 4m + а – 2m + 3а; 2) -5b + 9 + 4b;
3) -3x + 2у – 3у + 4x; 4) 7 – 2m + 3m.
1257. Зведи подібні доданки:
1) 7а – 3b – 5а + 4b;
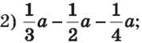
3) -5x + 9у – 7x – 8у; 4) 0,47m – 0,49m – 0,52m;
5) 18,2p + 9,2x – 9,7p; 6) a + b + a – b.
1258. Зведи подібні доданки:
1) 5m – 4n – 3m + 2n;
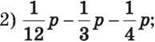
3) -2x + 3у – 3x + 5у; 4) 0,12a – 0,48a – 0,37a;
5) 12,9b + 13,7c – 4,5b; 6) m + t – m + t.
1259. На малюнку 85 AB = 3a; BC = 2a. Склади вираз для обчислення довжини відрізка АС. Спрости цей вираз та знайди його значення, якщо: 1) а = 3 см; 2) а = 8 дм.
Мал. 85
1260. На малюнку 85 AC = 7m; BC = 3m. Склади вираз для обчислення довжини відрізка AB. Спрости цей вираз та знайди його значення, якщо: 1) m = 4 см; 2) m = 5 дм.
1261. Розкрий дужки і зведи подібні доданки:
1) 2(3x – 5) + 4x; 2) – ( 7a + 8) + 3a;
3) 7x + (x – 3); 4) 2у – 3(у – 5).
1262. Розкрий дужки і зведи подібні доданки:
1) -2(3x – 5) + 8(2 – 4x); 2) -9(4a + m) + 5(m – 9a);
3) (4x – 0,5) ∙ 0,2 + (2x + 0,3) ∙ (-0,5);
4) 3,2(4b – 3a) – 2,8(b + 2a).
1263. Розкрий дужки і зведи подібні доданки:
1) -4(7 – 2x) + 6(3x – 5); 2) 2(a – 2b) – 7(2a + 3b);
3) (3m – 2) ∙ (-0,7) + (4 – 2m) ∙ 0,5;
4) 4,2(5x – 2у) – 2,7(3x – у).
1264. Спрости вираз та знайди його значення:
1) – (2m – 0,2) + 2(4m – 0,1), якщо m = 0,7;
2) 3(2x – 0,8) – (6x + 0,4), якщо x = 1,83.
1265. Спрости вираз та знайди його значення:
1) – (3а – 1,2) + 3(2а – 0,4), якщо а = 0,2;
2) 4(2m – 0,9) – (8m – 0,2), якщо m = 0,132.
1266. Спрости вираз:
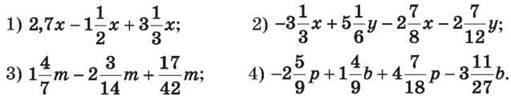
1267. Спрости вираз:
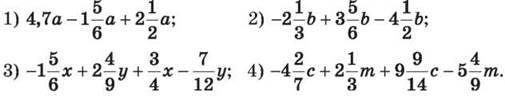
1268. Спрости вираз:
1) (-1,8а + 2,5b) ∙ 4 – 3(3,2а + 0,9b – 2) – (2,8а – 7);
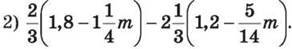
1269. Спрости вираз:
1) (-0,7x + 0,6у) ∙ 5 – 3(0,4у – 1,5x – 1) – (2,7x – 8);
1270. Розв’яжи рівняння:
1) 0,6x + 0,4x – 0,84x = 0,832;
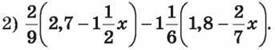
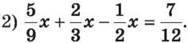
1271. Розв’яжи рівняння:
1) 0,47x – 0,5x + 1,3x = 15,24;
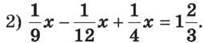
1272. Доведи, що значення виразу (2x – 3) ∙ 0,2 – (3x – 4) ∙ 0,5 – (2,6 – 1,1x) не залежить від значення змінної.
1273. Доведи, що значення виразу (3у – 0,8) ∙ 0,4 – 0,2(5 – 2у) – (1,6у – 0,8) не залежить від значення змінної.
1274. Знайди периметр многокутника, зображеного на малюнку 86. Спрости отриманий вираз та знайди його значення, якщо b = 8 см, c = 9 см.
1275. Доведи, що значення виразу 4(0,3x – 5,1) – 0,3(4x – 2,5) при будь-якому значенні змінної набуває від’ємного значення.
1276. Доведи, що значення виразу 0,6(18x – 7) – 1,8(6x – 4) при будь-якому значенні змінної набуває додатного значення.
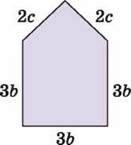
Мал. 86
1277. Доведи, що при будь-якому натуральному значенні n значення виразу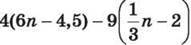 
кратне числу 7.
1278. Доведи, що при будь-якому натуральному значенні m значення виразу 9(3m – 8) + 2(25 – 11m) + 23 не ділиться на 5.
1279. Знайди значення виразу 9a – (3a + 2b), якщо 3a – b = 0,9.
1280. Знайди значення виразу -2x – (6y – 5x), якщо x – 2y = 0,4.
1281. Запиши три дроби, що дорівнюють дробу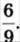 
1282. Порівняй числа:
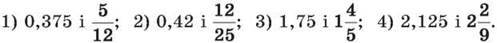
1283. Яка ймовірність того, що навмання вибране від 1 до 25 натуральне число буде простим?
1284. На малюнку 87 зображено цеглину. Як за допомогою трьох таких цеглин і лінійки (або рулетки) виміряти довжину відрізка AB?
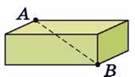
Мал. 87
Завдання для перевірки знань № 8 (§ 43 – § 46)
1. Знайди добуток: 1) 37 ∙ (-5); 2) -25 ∙ (-9).
2. Назви коефіцієнт буквеного виразу:
1) 7b; 2) -5а; 3) -0,8t; 4) p.
3. Зведи подібні доданки: 1) 4m – 5m; 2) 2у + 3у – 9у.
4. Виконай дії зручним способом:
1) -0,2 ∙ 39 ∙ (-5); 2) 4 ∙ 29 – 14 ∙ 29.
5. Обчисли: 1) (-4,2)2; 2) (-0,8)3.
6. Спрости: 1) -1,5а ∙ (-2b); 2) -5x + 3у + 7x – 9у.
7. Доведи, що значення виразу -0,6(x – 3,7) + 0,2(3x – 5) не залежить від значення змінної.
8. Розв’яжи рівняння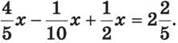 
9. Знайди значення виразу -8а – (4а – 6b), якщо b – 2а = -4.
Додаткові вправи
10. Розв’яжи рівняння (x – 1)(x + 2) = 0.
11. Знайди корінь рівняння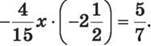 
12. Обчисли зручним способом 
(1 votes, average: 5.00 out of 5)
Loading...