Поворот
УРОК № 36
Тема. Поворот
Мета уроку: формування поняття повороту та вивчення властивостей повороту; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13].
Вимоги до рівня підготовки учнів: описують поворот; будує фігури, у які переходять дані фігури при повороті; застосовують вивчені означення і властивості до розв’язування задач.
Хід уроку
І. Перевірка домашнього завдання
Перевірити
Фронтальна бесіда
1) Дайте означення симетрії відносно прямої. 2) Які фігури називаються симетричними відносно осі (прямої)? Наведіть приклади. 3) Укажіть координати точки, яка симетрична точці А(а; b) відносно:
А) осі Ох; б) осі Оу.
4) Скільки осей симетрії має:
А) відрізок;
Б) промінь;
В) кут;
Г) пряма?
II. Поетапне сприймання й усвідомлення нового матеріалу
Поняття повороту
Поворотом фігури F навколо точки О на кут а називається таке перетворення, при якому будь-яка точка X фігури
XOX1= ? (рис. 167).
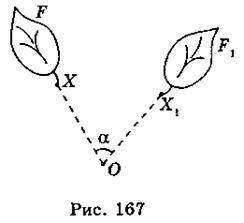
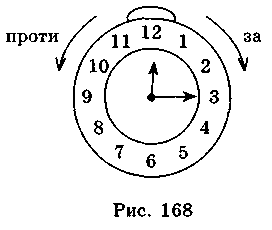
Поворот може здійснюватися за годинниковою стрілкою або проти годинникової стрілки (рис. 168). Поворот фігури задається кутом повороту і центром повороту.
Властивості повороту
1) Перетворення повороту є переміщенням. 2) Центральна симетрія є поворотом на 180°. 3) При повороті пряма переходить у пряму; кут – у рівний кут; відрізок – у рівний відрізок; будь-яка фігура переходить у рівну їй фігуру. 4) Правильний трикутник під час повороту навколо центра трикутника на 120° переходить у себе. Квадрат при повороті навколо центра квадрата на 90° (180°, 270°) переходить у себе. Правильний шестикутник при повороті навколо свого центра на 60° (120°, 180°, 240°, 270°) переходить у себе. Правильний многокутник при повороті навколо свого центра на кут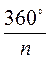 
переходить у себе. 5) Якщо точка В(х1; у1) є образом точки А(х; у) при повороті на 90° відносно початку координат:
А) за годинниковою стрілкою, то виконується умова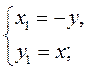 
Б) проти годинникової стрілки, то виконується умова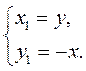 
Виконання вправ
1. Побудуйте довільні точки А, В, О. Виконайте поворот точок А і В навколо точки О на кут, який становить:
А) 45° за годинниковою стрілкою;
Б) 60° проти годинникової стрілки.
2. Побудуйте трикутник ABC і виберіть точку О поза ним. Виконайте поворот трикутника ABC навколо точки О на кут 90°:
А) за годинниковою стрілкою;
Б) проти годинникової стрілки.
III. Самостійна робота
Самостійну роботу навчального характеру можна виконати за посібником [14], тест 12 “Центральна та осьова симетрія”.
IV. Закріплення та осмислення нового матеріалу
Розв’язування задач
1. Дано коло (х – 1)2 + (у – 1)2 = 4. Запишіть рівняння кола, яке утворюється з даного внаслідок його повороту навколо початку координат на кут 90°:
А) за годинниковою стрілкою;
Б) проти годинникової стрілки.
2. Доведіть властивості повороту. 3. Дано пряму х + у = 1. Запишіть рівняння прямої, яка утвориться з даної внаслідок її повороту навколо початку координат на кут 90°:
А) за годинниковою стрілкою;
Б) проти годинникової стрілки.
V. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачу.
Запишіть рівняння кола, яке утворюється з кола (х + 1)2 + (у + 2)2 = 9 унаслідок його повороту навколо початку координат на кут 90°:
А) за годинниковою стрілкою;
Б) проти годинникової стрілки.
VI. Підбиття підсумків уроку
Запитання до класу
1. Яке переміщення називається поворотом? 2. Сформулюйте властивості повороту.
(1 votes, average: 5.00 out of 5)
Loading...