Головна ⇒ 📌Формули й таблиці ⇒ Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ
Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ
Формули й таблиці
МАТЕМАТИКА
ПРОПОРЦІЇ. ВІДСОТКИ
Правила диференціювання
Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних:
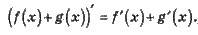
Правило 2. Якщо функція у = f(x) має похідну в точці х, то і функція y = kf(х) має похідну в точці х, до того ж:
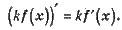
Правило 3. Якщо функції y = f(x) і у = g(x) мають похідну в точці x, то і їхній добуток має похідну в точці х, до того ж:
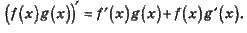
Правило 4. Якщо функції у = f(х) і у = g(x) мають похідну в точці х, у якій g(x) ≠ 0, то й частка f(x)/g(x) має похідну в точці х, до того ж:
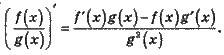
Related posts:
- Правила знаходження первісних – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила знаходження первісних Правило 1. Якщо функції у = f(x) і у = g(x) мають на числовому проміжку X первісні, відповідно у = F(x) й у = G(x), то і сума функцій у = f(x) + g(x) має на проміжку X первісну у= =F(x) + G(x). (Первісна суми дорівнює […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
- Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...
- Похідні елементарних функцій – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Похідні елементарних функцій Y = f(x) Y = f'(x) Y = f(x) Y = f'(x) Y = c (c = const) Y’ = 0 У = ax + b Y’ = a Y = xn Y’ = nxx-1 Y = x Y’ = 1 Y = 1/x Y’ = […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Відношення та пропорції Математика – Алгебра Множення і ділення звичайних дробів Відношення та пропорції Відношенням двох чисел називається частка цих чисел. Відношення показує, у скільки разів одне число більше від другого або яку частину становить одне число від другого. Щоб знайти відношення двох величин, вони мають бути виміряні однією й тією ж одиницею вимірювання. Наприклад, відношення 3 км […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Пропорція, члени пропорції. Основні властивості пропорції Урок № 4 0 Тема. Пропорція, члени пропорції. Основні властивості пропорції Мета: сформувати уявлення учнів про зміст понять пропорція, члени пропорції, основна властивість пропорції та виробити вміння застосовувати ці поняття під час розв’язування типових завдань, що передбачають їх застосування. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань @ […]...
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....
- Розв’язування рівнянь на основі властивостей пропорції Урок № 4 1 Тема. Розв’язування рівнянь на основі властивостей пропорції Мета: закріпити знання, набуті на попередньому уроці, виробити вміння і відпрацювати стійки навички розв’язування рівнянь на основі властивості пропорції. Тип уроку: формування вмінь і навичок. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Закінчіть речення: “Рівністю двох відношень називають…” [Якщо […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Пропорція. Основна властивість пропорції Розділ 3 Відношення і пропорції §21. Пропорція. Основна властивість пропорції Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність Рівність двох відношень називають пропорцією. Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так: Ці […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ВІДСОТКИ Цілі: – навчальна: удосконалити вміння застосовувати поняття відсотка, правила знаходження відсотків від числа та числа за його відсотками до розв’язування задач; перевірити рівень засвоєння знань учнів з теми “Відсотки” шляхом проведення самостійної роботи; – розвивальна: розвивати творчі здібності, кмітливість учнів; – виховна: виховувати інтерес до вивчення математики, відповідальність за результати роботи; Тип уроку: застосування знань, […]...
- МАТЕМАТИКА Формули й таблиці МАТЕМАТИКА Натуральні числа Натуральні – числа 1, 2, 3, що використовуються для рахунку предметів. Позначається буквою N. Просте число – натуральне число, що має тільки 2 дільники: самого себе й одиницю. Таких чисел нескінченна множина. Якщо число n – це добуток двох чисел: n = m · k, то воно ділиться без […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- ВІДСОТКИ. СЕРЕДНЄ АРИФМЕТИЧНЕ ЗАДАЧІ НА ПОВТОРЕННЯ ВІДСОТКИ. СЕРЕДНЄ АРИФМЕТИЧНЕ 120. 52% всіх учнів музичної школи навчаються грати на фортепіано, 28% – на скрипці. Скільки учнів навчаються по класу фортепіано, а скільки – по класу скрипки, якщо всього у школі 250 дітей? 121. Поле площею 150 га на 72% засаджено цукровими буряками. Скільки гектарів поля засаджено буряками? 122. Площа […]...
- Відсотки. Знаходження відсотків від числа Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 5. ДЕСЯТКОВІ ДРОБИ 37. Відсотки. Знаходження відсотків від числа На практиці люди часто користуються сотими частинами величин. Наприклад, сота частина гектара – 1 ар (1 сотка), сота частина століття – 1 рік, сота частина гривні – 1 копійка, сота частина метра – 1 сантиметр. Для сотої […]...
- Диференціювання клітин, зародкових листків, тканин МЕДИЧНА БІОЛОГІЯ Розділ 1 БІОЛОГІЧНІ ОСНОВИ ЖИТТЄДІЯЛЬНОСТІ ЛЮДИНИ 1.3. Онтогенетичний рівень організації життя 1.3.3. Біологія індивідуального розвитку 1.3.3.6. Диференціювання клітин, зародкових листків, тканин Диференціювання – це процес, внаслідок якого клітина стає більш спеціалізованою, тобто набуває морфологічних і функціональних особливостей. Це зміни, які відбуваються у клітині впродовж одного, нерідко термінального, клітинного циклу. Прикладом може бути диференціювання […]...
- ДОВЕДЕННЯ ТОТОЖНОСТЕЙ Цілі: – навчальна: удосконалити вміння учнів доводити тотожності; – розвивальна: формувати вміння міркувати за аналогією; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати упевненість у власних силах, уміння самоорганізовуватися, спостережливість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ […]...
- ПОВТОРЕННЯ. ВІДСОТКИ. СЕРЕДНЄ АРИФМЕТИЧНЕ Цілі: – навчальна: повторити поняття відсотка; відтворити вміння знаходити відсотки від числа та число за його відсотками, розв’язувати задачі на відсотки; повторити поняття середнього арифметичного та середнього значення величин; відтворити вміння розв’язувати задачі, які передбачають використання цих понять; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип […]...
- Тематичне оцінювання № 9 по темі “Відсотки” Урок № 62 Тема. Тематичне оцінювання № 9 по темі “Відсотки” Мета уроку. Діагностика та контроль якості засвоєння відсотків. Хід уроку I. Організаційна частина На розсуд вчителя. II. Запис та виконання вправ і задач учнями ВАРІАНТ 1. 1).° Запишіть у вигляді звичайного і десяткового дробів: 9%, 31%, 105%, 180%. 2).° Записати у відсотках: 7/100, 3/10, […]...
- Завдання для перевірки знань до §§ 19-21 1. 1) у = х2 + х; 3) – функції. 2. 1) у = 3х – 7; 3) у = 4 – лінійні функції. 3. 1) у = -2х + 6; k = -2; l = 6; 2) у = 7,4x; k = 7,4; l = 0. 4. у = -2х + 7; 1) х […]...