Головна ⇒ 📌Довідник з геометрії ⇒ Правильні многокутники
Правильні многокутники
Геометрія
Многокутники
Правильні многокутники
Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні.
Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола.
Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним навколо кола.
Вписане й описане кола правильного многокутника мають один і той самий центр, який називається Центром многокутника.
– центральний кут многокутника.
;
;
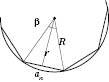
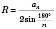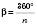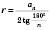.Теорема 2. Правильні опуклі n-кутники подібні. Зокрема, якщо у них сторони рівні, то такі n-кутники рівні.
Правильний трикутник (рівносторонній)
На рисунку:
;
;
; 
;
;
: 
; 
;
; 
;
; 
;
; 
; 
;
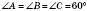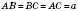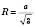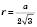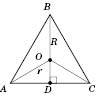
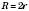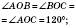
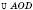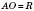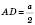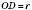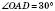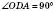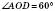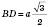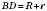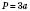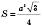.Правильний чотирикутник (квадрат)
На рисунку:
;
;
; 
;
; 
; 
;
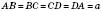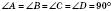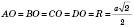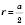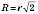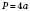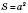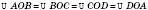– рівнобедрені прямокутні трикутники.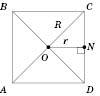
Правильний шестикутник
На рисунку:
;
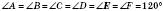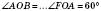; сторона а;
; 
;
; 
;
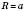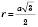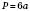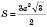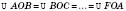– рівноcторонні трикутники;ABCD – рівнобічна трапеція з кутами
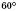і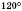 
;
, 
;
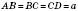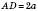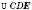– рівнобедрений;
; 
;
; 
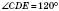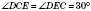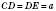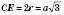.Діагональ
.
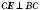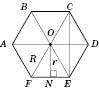
Зверніть увагу: якщо з’єднати послідовно середини сторін правильного n-кутника, отримаємо правильний n-кутник (див. рисунки).
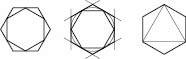
Якщо через вершини правильного n-кутника провести дотичні до описаного навколо нього кола, отримаємо правильний n-кутник.
Якщо з’єднати через одну вершини правильного 2n-кутника, отримаємо правильний n-кутник.
Related posts:
- Правильні многокутники УРОК № 17 Тема. Правильні многокутники Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 4. Вимоги до рівня підготовки учнів: формують означення правильного многокутника; застосовують вивчені означення до розв’язування задач. Хід уроку І. Перевірка домашнього завдання […]...
- Многокутники Геометрія Многокутники Ламаною … називається фігура, яка складається з точок , , ,…, і відрізків, що їх послідовно сполучають. Точки , , , …, називаються Вершинами ламаної, а відрізки ; ; …; – Ланками ламаної. Ламана називається Простою, якщо вона не має самоперетинів. Довжиною ламаної називається сума довжин її ланок. На рисунку 1 зображена проста […]...
- Многокутники. Рівні фігури Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 13. Многокутники. Рівні фігури На рисунках 107 і 108 зображено три фігури, кожна з яких обмежена замкненою ламаною, що складається з чотирьох ланок: АВ, ВС, CD і DA. Чим відрізняються межі фігур на рисунку 107 від межі фігури на рисунку […]...
- Формули радіусів вписаних і описаних кіл правильних многокутників УРОК № 18 Тема. Формули радіусів вписаних і описаних кіл правильних многокутників Мета уроку: Виведення формул для радіусів вписаних і описаних кіл правильного многокутника. Формування вмінь застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 5, 6. Вимоги до рівня підготовки учнів: записують і пояснюють формули радіусів вписаного та описаного кіл […]...
- Многокутники. Розв’язування задач і вправ Урок № 47 Тема: Многокутники. Розв’язування задач і вправ Мета. Дати означення ламаної, ввести поняття многокутника, ознайомити з видами многокутників, видами трикутників за сторонами, формувати навички застосовувати вивчений матеріал до розв’язування задач, сприяти формуванню логічного мислення, виховувати вміння самостійно аналізувати і робити висновки. Форми роботи: самостійна робота з підручником, усне опитування “Мозковий штурм”, метод інтерактивної […]...
- Многокутники. Розв’язування задач Урок № 49 Тема: Многокутники. Розв’язування задач Мета. Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал, до розв’язування задач, розвивати навички самостійної пізнавальної роботи, розвивати вміння самостійної роботи, розвивати вміння аналізувати, робити висновки. Форми роботи: математичний диктант, бесіда, розв’язування задач і виконання вправ. Обладнання: лінійка, кольорова крейда, косинець. Тип уроку: урок узагальнення і […]...
- Правильні многогранники 862. Якщо у піраміді всі ребра рівні, то з них можна скласти правильний октаедр. АB = а; AM = а; Відповідь: 863. А) так; б) так. 864. А) ні; б) так; в) ні. 865. Якщо з однієї вершини куба провести три діагоналі бічних граней і їх кінці з’єднати відрізками, то утворена піраміда буде тетраедром. 866. […]...
- Побудова правильних многокутників УРОК № 19 Тема. Побудова правильних многокутників Мета уроку: ознайомлення учнів з правилами побудови правильних многокутників (зокрема трикутників, чотирикутників і шестикутників). Тип уроку: комбінований. Вимоги до рівня підготовки учнів: будують правильний трикутник, чотирикутник і шестикутник. Хід уроку І. Перевірка домашнього завдання Двоє учнів відтворюють за відкидними дошками розв’язування домашніх задач 1 і 2, а в […]...
- Правильні багатокутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Правильні багатокутники N – число кутів; R1 – радіус описаного кола; R2 – радіус вписаного кола; α – центральний кут; β – внутрішній кут; γ – зовнішній кут; Правильним називається багатокутник, у якому всі сторони і всі внутрішні кути рівні між собою....
- Властивість точки, рівновіддаленої від сторін многокутника Урок 36 Тема. Властивість точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, вписане в многокутник” Хід уроку 1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку. Нехай ABCD […]...
- МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 9. МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ Подивіться на малюнок 98. Ви бачите, як від точки А послідовно відкладали відрізки АВ, ВС, CD і DE, а точки А і Е сполучили відрізком АЕ. Будь-які два із цих відрізків не перетинаються і не є частинами однієї прямої. […]...
- Ламана і многокутник Урок № 42 Тема. Ламана і многокутник Мета: сформувати в учнів поняття: – ламана та її елементи; – проста ламана; – многокутник та його елементи; – периметр многокутника; – опуклий многокутник; – внутрішній та зовнішній кути многокутника; – многокутник, вписаний у коло та многокутник, описаний навколо кола. Формувати вміння відтворювати означення вивчених понять; на готовому […]...
- Багатокутники. Рівні фігури УРОК 37 Тема. Багатокутники. Рівні фігури Мета: формування поняття многокутника, рівних фігур; навчити розпізнавати многокутники, наводити приклади рівних фігур. Тип уроку: засвоєння нових знань. Обладнання: індивідуальні набори карток для практичної роботи. Хід уроку І. Актуалізація опорних знань Запитання до класу 1. Яка з ліній на рис. 54 є ламаною? замкненою ламаною? Назвіть вершини і ланки […]...
- Сума кутів опуклого многокутника Урок № 43 Тема. Сума кутів опуклого многокутника Мета: закріпити знання змісту понять, вивчених на попередньому уроці. Працювати над засвоєнням учнями змісту та доведення теореми про суму кутів опуклою многокутника. Сформувати вміння: – відтворювати зміст вивченої теореми; – застосовувати теорему під час розв’язування задач на знаходження градусної міри кутів многокутників. Тип уроку: засвоєння нових знань, […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- СКЛАДАННЯ ПРИКЛАДІВ НА ДОДАВАННЯ І ВІДНІМАННЯ ЗА МАЛЮНКАМИ. МНОГОКУТНИКИ. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 33. СКЛАДАННЯ ПРИКЛАДІВ НА ДОДАВАННЯ І ВІДНІМАННЯ ЗА МАЛЮНКАМИ. МНОГОКУТНИКИ. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ Мета: формувати в учнів уміння складати рівності на додавання і віднімання за малюнками, порівнювати числа, розпізнавати многокутники у конфігурації декількох фігур; розвивати навички каліграфічного письма; виховувати старанність. Хід […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Рівні фігури Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 23. Рівні фігури Геометричні фігури можуть бути рівними. Якщо вирізану з картона деяку геометричну фігуру, наприклад многокутник, покласти на аркуш паперу, обвести по периметру і вирізати ще один многокутник, то одержимо рівні многокутники (рис. 159). Дві фігури, які можна накласти одна на […]...
- Властивість точки, рівновіддаленої від вершин многокутнику Урок 32 Тема. Властивість точки, рівновіддаленої від вершин многокутнику Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, описане навколо многокутника”. Хід уроку 1. Перевірити розв’язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку. Розв’язання […]...
- Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...
- Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
- ПРАВИЛЬНІ І НЕПРАВИЛЬНІ ДРОБИ Цілі: – навчальна: удосконалити вміння розв’язувати задачі, які передбачають використання поняття правильного і неправильного дробу; – розвивальна: формувати вміння аналізувати інформацію, узагальнювати її; – виховна: виховувати свідоме ставлення до навчання; Тип уроку: удосконалення знань і вмінь. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ ____________________________________________ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ 1. Перевірка завдання, заданого […]...
- Багатогранники. Правильні багатогранники 3. Найменша кількість ребер, що сходиться в одній вершині багатогранника – три. 4. В одній вершині багатогранника може сходитися безліч ребер. Розглянемо піраміду з n-кутником в основі. Яким би великим не було число п, Завжди можна побудувати піраміду, основа якої має n + 1 вершин. 5. Розглянемо трикутну піраміду. Кількість її ребер шість. Шість – […]...
- Геометричні тіла і многокутники 868. ABCD – тетраедр, 6 ребер, 4 вершини, 4 грані. 869. Многогранник A1A2A3A4A5, 5 граней, 5 вершин, 8 ребер. 870. Многогранник, 5 граней, 6 вершин, 9 ребер. 872. 873. Див. рис. з № 872 S пов. тетр.=36 см2, S грані = 36 : 4 = 9, SABCD = 9 см2, а = ? 874. ABCDA1B1C1D […]...
- Правильні і неправильні дроби. Порівняння дробів Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 4. ЗВИЧАЙНІ ДРОБИ 26. Правильні і неправильні дроби. Порівняння дробів Чи може чисельник дробу дорівнювати його знаменнику? Так, може. На рисунку 194 прямокутник поділили на 7 рівних частин і всі частини заштрихували. Отже, заштрихованими виявились площі прямокутника, тобто весь прямокутник. Таким чином, прямокутника дорівнюють 1 прямокутнику, […]...
- Многогранник Геометрія Многогранники Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається Опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини й поверхні опуклого многокутника називається Гранню. На рисунку нижче зліва зображений неопуклий многогранник; на рисунку справа – опуклий. […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...