Приклади графіків залежностей між величинами
Урок № 114
Тема. Приклади графіків залежностей між величинами
Мета: формувати в учнів уявлення про зміст поняття “графік залежності”, сформувати уміння “читати таблиці” й виконувати побудову графіків простих залежностей за даними, розміщеними в таблиці
Тип уроку: засвоєння нових знань
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Збираємо зошити із творчими роботами на перевірку
ІІІ. Актуалізація опорних знань
Усні вправи
1. Обчисліть:
Б) 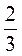 –
–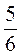
В) 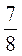 :
: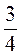
Г) 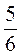 :
: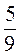
2 –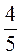
3 – 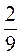
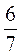 : 3
: 3
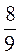 :
: 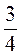
0,509 – 100
40 – 0,8
6,03 : 0,3
0,8 : 0,01
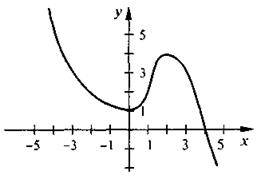
2. На координатній площині побудована лінія (див рис.):
А) Знайдіть на цій лінії точку, абсциса якої -3;
Б) Знайдіть точку, ордината якої
В) При яких значеннях х ордината у має найбільше (найменше) значення?
3. Ігровий момент
На магнітній дошці зображено систему координат До дошки викликається учень, який повинен швидко розмістити (приблизно) точку (магніт) у системі координат, щоб й координати задовольняли умови, які називає вчитель
Питання вчителя
А) х > 0, у > 0,
Б) х < 0, у < 0,
В) х > 0, у = 0,
Г) х = 0, у > 0,
Д) х < 0, у > 0,
Е) х = 0, у <0,
Є)* 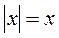 ,
,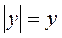 .
.
4. Температуру вимірювали впродовж доби через кожні 2 години За результатами вимірювань склали таблицю
Час доби год | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
Температура °С | 5 | 2 | 0 | -3 | -4 | -2 | 2 | 6 | 8 | 5 | 4 | 3 | 3 |
За результатами, занесеними в таблицю назвіть яка була температура о 6, 16, 24 год? О котрій годині температура була 3°С, 2°С, 8°С?
IV. Мотивація навчальної діяльності
Учитель. Друзі! Ви вже знаєте, що координатна площина відрізняється від звичайної площини тим, що на ній задано систему координат Система координат не дозволяє задати положення будь-якої точки на площині за допомогою двох чисел (її координат) Але виявляється, що цим фактом не обмежується “користь” системи координат У нашому повсякденному житті, в науці и техніці постійно розглядаються величини та залежності між ними мабуть, ваші батьки, спостерігаючи, як ви підростаєте, роблять помітки, якого зросту ви були в один, два, три і т. д. років, на уроках природознавства спостерігаєте за зміною температури упродовж місяця і т. ін.
Ви, мабуть, знаєте, що такі спостереження можна записувати у вигляді таблиці Тепер виникає питання, а чи можна “побачити” ці залежності (як міняється одна величина залежно від зміни іншої).
На це питання ми и будемо шукати відповідь далі.
V. Формування знань
Приклад 1. Температуру вимірювали через кожні дві години упродовж доби. За результатами вимірів дістали таку таблицю.
Час доби, год | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
Температура °С | 5 | 2 | 0 | -3 | -4 | -2 | 2 | 6 | 8 | 5 | 4 | 3 | 3 |
Якщо тепер побудувати систему координат, на осі абсцис позначити значення часу, а на осі ординат – температуру, дістанемо 13 точок, координати яких є відповідними числами з таблиці (0, 5), (2, 2), (4, 0), (6, -3), (8, -4), (10, -2), (12, 2), (14, 6), (16, 8), (18, 5), (20, 4), (22, 3), (24, 3). Маємо рисунок.
Якщо б ми вимірювали температуру частіше, скажімо кожні 15 хв або 5 хв, то дістали б набагато більше точок. Температура змінюється безперервно, але безперервно вимірювати її неможливо. Якщо припустити, що різких перепадів температури не було, ми зможемо здобуті точки сполучити неперервною лінією. Так ми дістали лінію, яку будемо називати графіком температури.
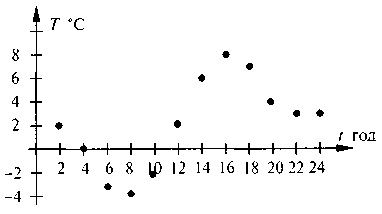
Приклад 2. Велосипедист рухався з постійною швидкістю 20 км/год Зобразити графік цього руху.
Відстань, яку проїхав велосипедист, маємо обчислити за формулою s = 20t (s = vt, де v = 20 км/год) Тепер знайдемо відстань, яку подолав велосипедист, наприклад, за 1 год, 2 год, 3 год, 4 год, 5 год, і запишемо ці числа в таблицю:
Час, год | 0 | 1 | 2 | 3 | 4 | 5 |
Відстань, км | 0 | 20 | 40 | 60 | 80 | 100 |
На осі абсцис будемо відкладати значення часу (1 од. відр. – 1 год), на осі ординат – відстань (1 од. відр. – 20 км) На координатній площині позначимо точки, координати яких є відповідними значеннями з таблиці. Отримані точки лежать на одній прямій. Сполучимо точки відрізками і дістанемо графік руху велосипедиста.
Отже, як побудувати графік будь-якої залежності, заданої у вигляді таблиці або формулою?
1. Знайдіть пари відповідних значень двох величин.
2. Побудуйте в системі координат точки, координати яких є відповідними значеннями двох змінних величин.
3. Сполучіть отриманні точки лінією – дістали шуканий графік.
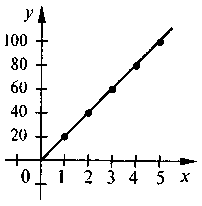
VI. Закріплення знань, вироблення вмінь
1. Побудуйте графік температури за даними таблиці:
Час, год | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Температура, °С | 4 | 2 | -1 | -2 | -3 | -3 | -1 | -1 |
2. Побудуйте графік руху за таблицею:
Час, год | 0 | 1 | 2 | 3 | 4 | 5 |
Відстань від початкового пункту, км | 0 | 2 | 4 | 6 | 8 | 10 |
3. Середня місячна температура повітря, °С:
Місто | Місяці | |||||||||||
І | ІІ | III | IV | V | VI | VII | VII | ІХ | X | XI | XII | |
Перм | -15 | -13 | -7 | 3 | 10 | 16 | 18 | 16 | 9 | 2 | -7 | -12 |
Рязань | -11 | -10 | -5 | 4 | 13 | 17 | 19 | 17 | 11 | 4 | -3 | -8 |
Мінськ | -7 | -6 | -2 | 5 | 13 | 16 | 18 | 16 | 12 | 6 | 0 | -5 |
Ростов-на-Дону | -5 | -7 | 0 | 9 | 11 | 20 | 23 | 22 | 16 | 9 | 3 | -4 |
Побудуйте графік середньомісячних температур для кожного міста.
(Вказівка. По осі Ох відкладайте час, прийнявши один одиничний відрізок за один місяць, а по осі Оу відкладайте значення температури, прийнявши за один одиничний відрізок 3°С.)
Додатково (на повторення)
Один робітник може виконати завдання за 10 год, а другий – за 60 % цього часу. Яка частина завдання залишиться невиконаною після трьохгодинної сумісної роботи обох робітників?
VII. Підсумки уроку
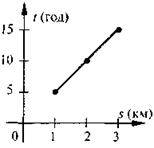
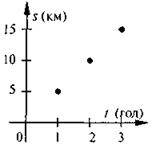
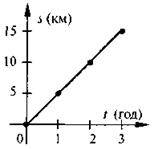
На якому з рисунків правильно побудовано таблицю і графік шляху пішохода зі швидкістю 5 км/год протягом 3 год?
1) s = 5t | 2) s = 5t | 3) s = 5t | |||||||||
T | 1 | 2 | 3 | T | 1 | 2 | 3 | T | 1 | 2 | 3 |
S | 5 | 10 | 15 | S | 5 | 10 | 15 | S | 5 | 10 | 15 |
VIII. Домашнє завдання
Вивчіть алгоритм побудови графіків температури та руху, виконайте задачі.
1. Побудуйте графік зміни температури заданими таблиці:
Час, год (координатах) | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
Температура, °С (координата у) | -3 | -5 | -6 | -4 | 0 | 1 | 3 |
2. Побудуйте графік руху пішохода за таблицею
Час, год (координатах) | 0 | 1 | 2 | 3 | 4 | 5 |
Відстань, км (координата у) | 0 | 6 | 12 | 18 | 24 | 30 |
(на осі Оу 1 од. відр. – 6 км)
3. Від села до міста легкова машина доїхала за 2 год, а вантажівка – за 5 год. Знайдіть швидкість руху кожної машини, якщо швидкість вантажівки на 48 км/год менша від швидкості легкового автомобіля (складіть рівняння).