Пряма й обернена теореми
Геометрія
Основні властивості найпростіших геометричних фігур
Пряма й обернена теореми
Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком.
Приклади
1) Якщо кути суміжні, то їх сума дорівнює 180°.
Умова Висновок
2) У прямокутному трикутнику центр описаного кола – середина гіпотенузи.
Умова: трикутник є прямокутним.
Висновок: центр описаного кола – середина
3) Дві прямі, паралельні третій, паралельні одна одній.
Дано (умова): прямі a, b, c;
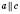 ;
;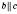 .
.Довести (висновок):
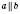 .
.Якщо умови й висновок теореми поміняти місцями, отримаємо теорему, яка називається Оберненою до даної (“прямої”) теореми. Такі дві теореми називають Взаємооберненими. Кожну з них можна назвати прямою, тоді інша буде оберненою. Інколи із цих двох теорем правильною є тільки одна.
Приклад
Пряма теорема. Якщо кути вертикальні, то вони рівні. (Правильно.)
Обернена теорема. Якщо кути рівні, то вони вертикальні.
Бувають випадки, коли правильними є обидві теореми.
Приклад
Пряма теорема. Кути при основі рівнобедреного трикутника рівні. (Правильно.)
Обернена теорема. Якщо два кути трикутника рівні, то він рівнобедрений. (Правильно.)
У таких випадках використовують словосполучення “тоді й тільки тоді”, “необхідно й достатньо”.
Приклади
1) Катет прямокутного трикутника тоді й тільки тоді дорівнює половині гіпотенузи, коли протилежний йому кут дорівнює
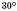 . (Це твердження містить одночасно пряму й обернену теореми.)
. (Це твердження містить одночасно пряму й обернену теореми.)2) Для того щоб прямі були паралельними, необхідно й достатньо, щоб внутрішні різносторонні кути були рівними.
Треба розуміти, що твердження “для того щоб прямі були паралельними, необхідно, щоб внутрішні різносторонні кути були рівними” означає властивість паралельних прямих.
Твердження “для того щоб прямі були паралельними, достатньо, щоб внутрішні різносторонні кути були рівними” означає ознаку паралельних прямих.