Головна ⇒ 📌Довідник з геометрії ⇒ Ознака паралельності площин
Ознака паралельності площин
Геометрія
Стереометрія
Ознака паралельності площин
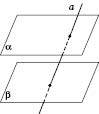
Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні.
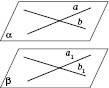
Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні.
Зверніть увагу: прямі мають обов’язково перетинатися. Дійсно, в площині  може бути скільки завгодно прямих, паралельних
може бути скільки завгодно прямих, паралельних
 , і при цьому площини
, і при цьому площини  і
і  не будуть паралельними.
не будуть паралельними.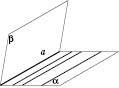
Теорема 3. Якщо пряма перетинає одну з двох паралельних площин, то вона перетинає й другу (див. рисунок).
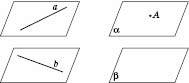
Теорема 4. Через дві мимобіжні прямі можна провести паралельні площини (рисунок нижче зліва).
Теорема 5. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну (рисунки нижче).
Теорема 6. Якщо дві площини паралельні третій, то вони паралельні одна одній.




 (3 votes, average: 5.00 out of 5)
(3 votes, average: 5.00 out of 5)Related posts:
- Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Урок 15 Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин. Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”. Хід уроку 1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Ознака паралельності прямих Геометрія Стереометрія Ознака паралельності прямих Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). Зверніть увагу: якщо ABCD – просторовий чотирикутник, то його діагоналі AC і BD – мимобіжні прямі....
- Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Ознака паралельності прямих Урок 9 Тема. Ознака паралельності прямих Мета уроку: вивчення ознаки паралельності прямих, формування умінь застосовувати ознаку паралельності до розв’язування задач. Обладнання: моделі прямокутного паралелепіпеда і куба. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язання задач № 5 (1, 3) та 7 (1, 3). 2. Проведення тесту на визначення істинності математичних тверджень. Тест […]...
- Паралельність прямих і площини Геометрія Стереометрія Паралельність прямих і площини Дві прямі в просторі називаються Паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються Мимобіжними. Зверніть увагу: “не лежать в одній площині” і “лежать у різних площинах” – це різні твердження. Наприклад, паралельні прямі a і b лежать у різних […]...
- Властивості паралельних площин Урок 18 Тема. Властивості паралельних площин Мета уроку: формування знань учнів про властивості паралельних площин. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування задачі № 24, у цей час клас пише математичний диктант. 2. Математичний диктант. Дано зображення куба: варіант 1 – рис. 64, варіант 2 – рис. 65. […]...
- Перпендикулярні площини. Ознака перпендикулярності площин Урок 38 Тема. Перпендикулярні площини. Ознака перпендикулярності площин Мета уроку: формування поняття перпендикулярності площин. Вивчення ознаки перпендикулярності площин. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Перевірити виконання задач № 49, 50 за записами, зробленими до початку уроку на дошці. Нехай AB?; А?, d?; АВ = b, ACD, AC = a (рис. […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- Існування площини, паралельної даній площині Урок 17 Тема. Існування площини, паралельної даній площині Мета уроку: вивчення теореми про існування єдино! площини, яка паралельна даній площині і проходить через дану точку, що не належить даній площині. Обладнання: стереометричний набір. Хід уроку Перевірка правильності розв’язування задачі № 25. Через дану точку А проведемо дві довільні прямі а і b, паралельні площині а […]...
- Ознака мимобіжності прямих Урок 10 Тема. Ознака мимобіжності прямих Мета уроку: вивчення ознаки мимобіжності прямих, формування вмінь застосовувати ознаку мимобіжності двох прямих до розв’язування задач. Обладнання: стереометричний набір, моделі тетраедра і куба. 1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час виконання цих завдань. 2. Самостійна робота. 1) Трикутник АВС і паралелограм […]...
- Розв’язування задач на застосування ознаки перпендикулярності площин Урок 39 Тема. Розв’язування задач на застосування ознаки перпендикулярності площин Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності площин до розв’язування задач. Обладнання: стереометричний набір. Хід уроку Фронтальна бесіда за контрольними запитаннями № 11-12 та перевірка виконання задач № 59 (2; 4; 6), 60. Розв’язання задачі № 59 (напівусне) Перпендикулярні площини? і? перетинаються […]...
- Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Урок 8 Тема. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Мета уроку: вивчення теореми про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Які прямі в просторі називаються паралельними? 2) Вкажіть […]...
- ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...
- Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...
- Тематичне оцінювання № 1 Урок 12 Тема. Тематичне оцінювання № 1 Мета уроку: перевірка навчальних досягнень учнів з тем “Вступ до стереометрії” та “Взаємне розміщення прямих у просторі”. Хід уроку Тематичне оцінювання № 1 можна провести, враховуючи результати виконання самостійної роботи на уроці № 6 та результати контрольної роботи. 1. Тематична контрольна робота № 1 Варіант А Варіант 1 […]...
- Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...
- Взаємне розміщення двох прямих у просторі Урок 7 Тема. Взаємне розміщення двох прямих у просторі Мета уроку: вивчення взаємного розташування двох прямих у просторі: прямі, що перетинаються; паралельні прямі; мимобіжні прямі. Формування понять: паралельні прямі, мимобіжні прямі. Обладнання: стереометричний набір, каркасна модель куба, схема “Взаємне розміщення двох прямих у просторі”. Перевірку правильності виконання домашньої задачі провести шляхом фронтальної бесіди за записами, […]...
- Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Паралельні прямі. Властивості паралельних прямих Урок № 110 Тема. Паралельні прямі. Властивості паралельних прямих Мета: закріпити знання учнів про властивості паралельних прямих; відпрацювати навички розв’язування задач, що передбачають застосування набутих з теми знань; продовжувати роботу з повторення вивченого у 6 класі матеріалу. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Математичний диктант […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Урок 27 Тема. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Мета уроку: формування поняття прямої, перпендикулярної до площини. Вивчення ознаки перпендикулярності прямої і площини. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Відповіді на запитання, які виникли в учнів при виконанні домашнього завдання. 2. Самостійна робота. Варіант 1 1) Промені OВ, ОС, OD […]...
- Кут між мимобіжними прямими Геометрія Стереометрія Кут між мимобіжними прямими Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює за означенням. Кут між паралельними прямими вважаємо таким, що дорівнює нулю. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним […]...
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Паралельне проектування та його властивості. Зображення просторових фігур на площині Урок 21 Тема. Паралельне проектування та його властивості. Зображення просторових фігур на площині Мета уроку: формування знань про паралельне проектування. Вивчення властивостей паралельного проектування. Дати уявлення про зображення просторових фігур на площині. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Відповісти на запитання, які виникли в учнів при розв’язуванні домашньої задачі. 2. Самостійна […]...
- Побудова перпендикулярних прямих і площин Урок 29 Тема. Побудова перпендикулярних прямих і площин Мета уроку: формування вмінь учнів будувати перпендикулярні прямі і площини. Обладнання: стереометричний набір. Хід уроку 1. Перевірити правильність виконання задачі № 8 за записами (з пропусками), зробленими на дошці до початку уроку. Нехай у трикутнику АВС (C = 90°) АС = … , ВС = … , […]...
- Паралельні прямі Розділ 4 Раціональні числа і дії мідними §52. Паралельні прямі Дві різні прямі, побудовані на аркуші паперу або дошці, можуть перетинатися в одній точці (мал. 104) або не перетинатися (мал. 105). Аркуш паперу, дошка дають уявлення про площину. Також уявлення про площину дають поверхня стола, шибка тощо. Мал. 104 Мал. 105 Мал. 106 – Дві […]...
- Існування площини, яка проходить через три дані точки УРОК 4 Тема. Існування площини, яка проходить через три дані точки Мета уроку: вивчення теореми про існування єдиної площини, яка проходить через три дані точки, які не лежать на одній прямій. Обладнання: стереометричний набір, моделі куба і тетраедра. Хід уроку 1. Один із учнів відтворює розв’язування задачі № 10, решта класу пише математичний диктант. 2. […]...
- Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...
- Властивості прямої і площини, перпендикулярних між собою Урок 30 Тема. Властивості прямої і площини, перпендикулярних між собою Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин. Обладнання: стереометричний набір, схема “Властивості прямо і площини, перпендикулярних між собою” (с. 116). Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення розв’язування задачі № 10. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Властивості паралельних прямих Урок № 8 Тема. Властивості паралельних прямих Мета: домогтися засвоєння учнями змісту таких понять: “теорема”, “доведення теореми”, “умова і висновок теореми”, а також алгоритму доведення методом від супротивного; використовуючи метод доведення “від супротивного”, довести терему про дві прямі, паралельні третій. Сформувати вміння: – відтворювати означення основних понять уроку; – застосовувати названі поняття під час розв’язування […]...
- Кут між мимобіжними прямими Урок 53 Тема. Кут між мимобіжними прямими Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими. Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда. Хід уроку II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання. III. Сприйняття й […]...
Одяг »