Головна ⇒ 📌Математика ⇒ ПРЯМА ПРОПОРЦІЙНІСТЬ

ПРЯМА ПРОПОРЦІЙНІСТЬ

РОЗДІЛ 4 ФУНКЦІЇ

&18. ПРЯМА ПРОПОРЦІЙНІСТЬ

Ви знаєте, що залежність вартості р цукерок від їх кількості т, якщо їх ціна становить 25 грн за кілограм, можна виразити формулою р = 25m, або в загальному вигляді у = kх. Така залежність є особливим випадком лінійної функції y = Kх + b, коли b = 0, a k ≠ 0. Кожне значення такої функції пропорційне відповідному значенню її аргументу з коефіцієнтом пропорційності к.

Запам’ятайте!

Функція, яку можна задати формулою виду у = kх, де х – аргумент, k – число (k ≠ 0), називається прямою пропорційністю.

?

Чому не можна вважати прямою пропорційністю функцію у = kx, якщо k = 0? Тому що за такого значення коефіцієнта k дана функція є сталою. Тобто зі зміною аргументу значення функції не змінюється, а отже, немає пропорційної залежності у від х.

Оскільки пряма пропорційність є різновидом лінійної функції, то вона має всі властивості останньої. Розглянемо особливі властивості прямої пропорційності.

1. Пара чисел (0; 0) задовольняє формулу у = kx за будь-якого значення k. Тому графік прямої пропорційності завжди проходить через початок координат (мал. 50).

2. Графік прямої пропорційності не може збігатися з віссю ординат,

оскільки будь-яка пряма, перпендикулярна до осі абсцис, не відображає функціональної залежності.

3. Графік прямої пропорційності не може збігатися з віссю абсцис, оскільки функція у = 0 не є прямою пропорційністю.

Звідси випливає, що кожна пряма, яка проходить через початок координат і не збігається з осями координат, с графіком прямої пропорційності.

ПРЯМА ПРОПОРЦІЙНІСТЬ

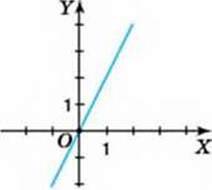
Мал. 50

Запам’ятайте!

Властивості функції у = kх:

1) область визначення – усі числа;

2) область значень – усі числа;

3) функція зростає, якщо k > 0;

4) функція спадає, якщо k < 0;

5) графіком є пряма, що проходить через початок координат;

6) графік не збігається з осями координат.

? Чи можна вважати число k кутовим коефіцієнтом прямої пропорційності? Так, оскільки пряма пропорційність є окремим випадком лінійної функції.

Подивіться на малюнки 51 і 52. Ви бачите графік функції у = 0,5х (мал. 51) і графік функції у = -0,5x (мал. 52). Перший графік утворює з додатним променем осі ОХ гострий кут, а другий графік – тупий кут. Формули, що задають ці функції, відрізняються знаком коефіцієнта k: у першої функції k > 0, а в другої – k < 0.

ПРЯМА ПРОПОРЦІЙНІСТЬ

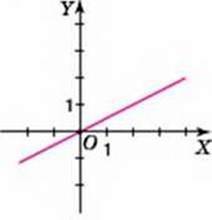
Мал. 51

ПРЯМА ПРОПОРЦІЙНІСТЬ

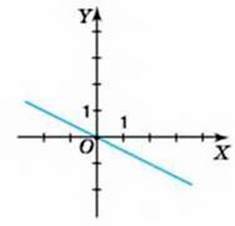
Мал. 52

Зверніть увагу:

Графік функції у = kx утворює з додатним променем осі ОХ:

– гострий кут, якщо k > 0;

– тупий кут, якщо k < 0.

Дізнайтеся більше

1. Владислав Кирилович Дзядик (1919 – 1998) – український математик, доктор фізико-математичних наук (1960), професор, член-кореспондент НАН України (з 1969 р.), Соросівський професор.

Народився в смт. Сахновщина Харківської області. Вищу освіту здобув на механіко-математичному факультеті Дніпропетровського університету (1951).

Працював учителем у школі на Волині, викладачем у Луцькому педагогічному інституті та Київському університеті, а з 1960 – в Інституті математики НАН України. У 1963 році створив відділ теорії функцій Інституту математики, яким керував до 1990 року. Цей відділ існує й дотепер. В. К. Дзядик довгий час працював переважно в галузі теорії функцій. Розробив спеціальні математичні методи та перетворення, які названо на його честь “методи Дзядика” і “перетворення Дзядика”.

ПРЯМА ПРОПОРЦІЙНІСТЬ

2. Нехай функцією у = kx задано залежність шляху у, який проходить той чи інший об’єкт, від часу х. Значення цієї функції може змінюватися в часі або швидше, або повільніше, залежно від значення коефіцієнта функції:

– для k > 0 – що більше k, то швидше збільшується значення функції;

– для k < 0 – що менше k, то швидше зменшується значення функції.

Виходить, що коефіцієнт k показує, наскільки швидко змінюється функція у = kx. Тому по-іншому цей коефіцієнт називають швидкістю зміни функції “пряма пропорційність”. Спираючись на графіки функцій, наприклад, для k > 0 (див. мал. 50, 51), можна сказати і так: що більша швидкість зміни функції у = kx, то “крутіший” її графік.

Наприклад, якщо у функцію y = kx замість коефіцієнта k підставити значення швидкості сапсана (320 км/год), літака (наприклад, для Ан-124 Руслан – це 865 км/год) і супутника (28 440 км/год), то очевидно, що найшвидше функція, яка задає залежність шляху від часу, зростає в супутника, а найповільніше – у сапсана (мал. 53-55).

ПРЯМА ПРОПОРЦІЙНІСТЬ

Мал. 53

ПРЯМА ПРОПОРЦІЙНІСТЬ

Мал. 54

ПРЯМА ПРОПОРЦІЙНІСТЬ

Мал. 55

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Яка функція називається прямою пропорційністю?

2. Назвіть властивості прямої пропорційності.

3. Що є графіком прямої пропорційності?

4. Які властивості графіка прямої пропорційності?

5. У якому випадку графік функції у = kx утворює з додатним променем осі ОХ гострий кут; тупий кут?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

946. Чи правильно, що функція y = kx + b є прямою пропорційністю, якщо:

1) k = 0; 2)b = 0,k ≠ 0; 3) k = 1; 4) b = 1?

947. Чи правильно, що графіком прямої пропорційності є пряма, яка:

1) паралельна осі абсцис; 5) проходить через початок

2) паралельна осі ординат; координат і не збігається з

3) збігається з віссю ординат; осями координат?

4) збігається з віссю абсцис;

948. На якому з малюнків 56-58 зображено графік прямої пропорційності?

ПРЯМА ПРОПОРЦІЙНІСТЬ

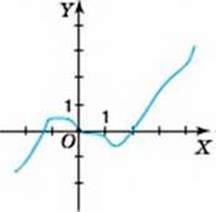
Мал. 56

ПРЯМА ПРОПОРЦІЙНІСТЬ

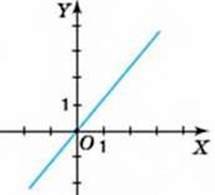
Мал. 57

ПРЯМА ПРОПОРЦІЙНІСТЬ

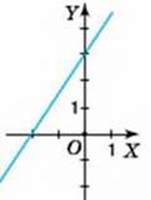
Мал. 58

949. Чи правильно, що точка О (0; 0) належить графіку функції:

1)у = 3х – 3; 2)у = 2х; 3)у = 5?

950. Назвіть кутовий коефіцієнт функції:

1) y = 4х; 2) у = -0,7х; 3) y = ПРЯМА ПРОПОРЦІЙНІСТЬX.

951. Чи правильно, що дана функція зростає:

1) у = -3х; 2)у = 2х; 3)у = 5?

952. Чи правильно, що дана функція спадає:

1)у = 4х; 2) у = -7х; 3)у = -6?

953. Який кут – тупий чи гострий – утворює з додатним променем осі ОХ графік функції:

1)у = 3х; 2)у = -7х; 3)у = -0,6х?

954. Чи є прямою пропорційністю дана функція:

1) у = – t + 2; 2) x = 4t; 3) t = -2?

Відповідь поясніть.

955. Яка з точок A (1; 1), В (2; 2), С (-3; 3), D (2; -2), E (-2; -2) належить графіку функції у = х?

956 . Яка з точок A (1; 2), В (2; 1),С (-3; 6), D (-3; -6), Е (-2; -1) належить графіку функції у = 2х?

957. На малюнку 59 зображено графік прямої пропорційності. Користуючись графіком, знайдіть:

1) значення у, якщо х = -1; 0; 1; 2;

2) значення х, за якого у = 0;

3) три значення аргументу, за яких значення функції додатне;

4) три значення аргументу, за яких значення функції від’ємне.

ПРЯМА ПРОПОРЦІЙНІСТЬ

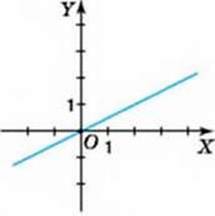
Мал. 59

958. На малюнку 60 зображено графік прямої пропорційності. Користуючись графіком, знайдіть:

1) значення у, якщо х = -2; -1; 0; 1;

2) значення х, за якого у = 0;

3) три значення аргументу, за яких значення функції додатне;

4) три значення аргументу, за яких значення функції від’ємне.

ПРЯМА ПРОПОРЦІЙНІСТЬ

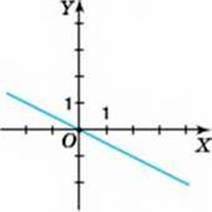
Мал. 60

959. Функцію задано формулою у = 3х. Накресліть у зошиті таблицю 25 та заповніть її.

Таблиця 25

X

-2

-1

0

1

2

Y

960. Відомо, що деяка функція є прямою пропорційністю з кутовим коефіцієнтом k = 1,5. Виконайте такі завдання:

1) задайте дану функцію формулою;

2) складіть таблицю значень функції для всіх цілих значень аргументу від -3 до 6;

3) побудуйте графік даної функції.

961. Відомо, що деяка функція є прямою пропорційністю з кутовим коефіцієнтом k = -2,1. Виконайте такі завдання:

1) задайте дану функцію формулою;

2) складіть таблицю значень функції для всіх цілих значень аргументу від -4 до 3;

3) побудуйте графік даної функції.

962. Чи проходить через початок координат графік функції:

1) у = 5х – 1; 2)у = -3х + 1; 3) у = 1; 4) у = –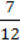ПРЯМА ПРОПОРЦІЙНІСТЬХ?

963. Чи належить графіку функції у = ПРЯМА ПРОПОРЦІЙНІСТЬ х точка:

1)A (3;-2, 5); 2) В (6; 1); 3) С (6; 5); 4)25 (12; 10)?

964. Чи належить графіку функції у = -1,3х точка:

1)K (-1; 1,3); 2)L(1; 1,3); 3) М (3; 3,9); 4) N (-3; 3,9)?

965. Яка з точок М (-1; -0,4), N (1; -0,4), Р (5; 2), R (-5; 2) належить графіку функції у = -0,4х?

966. Знайдіть будь-які три точки, що належать графіку функції:

1) у = -1,2х; 2) у = 3,5х; 3) у = –ПРЯМА ПРОПОРЦІЙНІСТЬХ.

967. Побудуйте графік функції:

1) y = х; 2) у = -3х; 3) у = 0,25х.

968. Побудуйте графік функції:

1) y = 4х; 2) у =-2х, 3) у = –ПРЯМА ПРОПОРЦІЙНІСТЬХ.

969. Графік функції у = nх проходить через точку М (-2; 5). Знайдіть значення n.

970. Графік функції y = kx проходить через точку К (-3; 2). Знайдіть значення k.

971. Графік функції у = bх проходить через точку В (-1; ПРЯМА ПРОПОРЦІЙНІСТЬ). Знайдіть значення b.

972. Задайте формулою функцію, що є прямою пропорційністю, якщо її графік проходить через точку:

1)А(1; 4); 3) С (-2;-3); 5)E(3;-2);

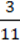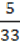2) В (-2; 5); 4)D(2; -1); 6) F (-ПРЯМА ПРОПОРЦІЙНІСТЬ; ПРЯМА ПРОПОРЦІЙНІСТЬ).

Побудуйте графік одержаної функції.

973. Задайте формулою функцію, що є прямою пропорційністю, якщо її графік проходить через точку:

1)А (2; 7); 2) В (-6; 4); 3) С (-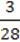ПРЯМА ПРОПОРЦІЙНІСТЬ; ПРЯМА ПРОПОРЦІЙНІСТЬ).

Побудуйте графік одержаної функції.

974. Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку, ордината якої втричі менша від відповідної абсциси. Побудуйте графік одержаної функції.

975. Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку, абсциса якої у 8 разів більша за відповідну ординату. Побудуйте графік одержаної функції.

976. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт дорівнює середньому арифметичному всіх парних додатних одноцифрових чисел. Побудуйте графік одержаної функції.

977. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт є числом, протилежним десятій частині середнього арифметичного всіх двоцифрових чисел, кратних числу 5 і менших від числа 42. Побудуйте графік одержаної функції.

978. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт є числом, протилежним дев’ятій частині середнього арифметичного всіх двоцифрових чисел, кратних числу 9 і менших від числа 55. Побудуйте графік одержаної функції.

979. Задайте формулою пряму пропорційність, графік якої проходить через точку:

1) A (-1; ПРЯМА ПРОПОРЦІЙНІСТЬ); 2) B (4,4; – 5,5); 3) C (2ПРЯМА ПРОПОРЦІЙНІСТЬ; 1ПРЯМА ПРОПОРЦІЙНІСТЬ).

Побудуйте графік одержаної функції.

980. Побудуйте графік функції:

1)у = 2|х|; 2) у = -4|х| – х; 3) у =3 |х – 1 |- 3х – 3.

981. Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку, ордината якої на 3 більша за абсцису, а кутовий коефіцієнт є цілим числом. Скільки випадків треба розглянути? Побудуйте графіки всіх одержаних функцій.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

982. Щодня магазин продає товару на суму 8000 грн. Запишіть у вигляді формули залежність кількості грошей, одержаної за проданий товар від кількості робочих днів. Визначте, на яку суму грошей у магазині буде продано товару за місяць, якщо в ньому було 28 робочих днів. Побудуйте графік одержаної функції.

983. Щоб покласти 1 м2 плитки майстер використовує 2 кг спеціального будівельного клею. Задайте формулою залежність маси клею від площі стіни, яку треба облицювати плиткою. Визначте, скільки клею знадобиться для облицювання у ванній кімнаті трьох стін прямокутної форми з розмірами 2,5 м х 3 м кожна.

ЗАДАЧІ НА ПОВТОРЕННЯ

984. Скільки триметрових стрибків потрібно зробити кенгуру, щоб подолати шлях завдовжки 450 м + 450 дм + 450 см + 450 мм?

985. Пeршe число в 3,5 рази більше за друге, а третє – на 2,8 менше від першого. Середнє арифметичне трьох чисел дорівнює 13,2. Знайдіть ці числа.

986. Розв’яжіть рівняння:

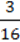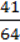(ПРЯМА ПРОПОРЦІЙНІСТЬ – y) ∙ 1ПРЯМА ПРОПОРЦІЙНІСТЬ = ПРЯМА ПРОПОРЦІЙНІСТЬ + ПРЯМА ПРОПОРЦІЙНІСТЬ.

987. Знайдіть найбільше трицифрове число, якщо воно ділиться на 3, 5, 9 і його запис містить цифру 7.

ПЕРЕВІРТЕ, ЯК ЗАСВОЇЛИ МАТЕРІАЛ

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Поясніть, як побудувати прямокутну систему координат на площині.

2. Яку назву мають осі координат; точка їх перетину?

3. Що називають координатною площиною?

4. Поясніть, як визначити координати точки.

5. Які координати має початок координат?

6. На скільки координатних чвертей розбивають площину координатні осі?

7. Сформулюйте означення функції.

8. Що називають аргументом функції?

9. Що таке область визначення функції?

10. Що таке область значень функції?

11. Назвіть способи задания функцій.

12. Що називають графіком функції?

13. Чи будь-яка геометрична фігура може бути графіком функції?

14. Як побудувати графік функції?

15. Як визначити, чи належить точка графіку функції?

16. Поясніть, яка функція називається зростаючою? Спадною?

17. Яка функція називається лінійною?

18. Що є графіком лінійної функції?

19. Як побудувати графік лінійної функції?

20. За яких значень k лінійна функція у = kx + b є зростаючою; спадною; сталою?

21. Як характеризує лінійну функцію число b?

22. Яка функція називається прямою пропорційністю?

23. Яка пряма є графіком прямої пропорційності?

24. У якому випадку графік функції y = kx утворює з додатним променем осі ОХ гострий кут; тупий кут?

25. Яке число називають кутовим коефіцієнтом?

ТЕСТОВІ ЗАВДАННЯ

Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового завдання потрібно 10-15 хв.

1. Знайдіть значення функції у = 2х2 – 3, якщо х = -2.

А.-5.

Б. 5.

В. 1.

Г.-11.

2. У якій точці перетинає вісь абсцис графік функції у = 5х – 12?

A. A (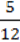ПРЯМА ПРОПОРЦІЙНІСТЬ; 0). Б. B (0; 12). B. C(2,4; 0). Г. D (0; ПРЯМА ПРОПОРЦІЙНІСТЬ).

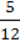3. Яка з точок А (-1; -1), В (-1; -3), С (-1; 1) чи D (1; -1) належить графіку функції у = -2х3 + 1?

А. А Б. В. B. C. Г. D.

4. На малюнку 61 зображено графіки чотирьох лінійних функцій а(х), b(х), с(х) і d(x). У яких функцій кутові коефіцієнти додатні?

ПРЯМА ПРОПОРЦІЙНІСТЬ

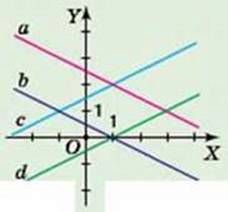
Мал. 61

A. а і с.

Б. b i d.

B. a i b.

Г. c i d.

5. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт є числом, протилежним до середнього арифметичного всіх додатних двоцифрових чисел, кратних числу 4 і менших від числа 41.

А. у = 24х + b. В. у = -220х.

Б. у = -26 х. Г. у = -40х.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Пряма пропорційність Розв’яжіть задачі 946. 1) ні; 2) так; 3) ні; 4) ні. 947. 1) ні; 2) ні; 3) ні; 4) ні; 5) так. 948. малюнок 57. 949. 1) ні; 2) так; 3) ні. 950. 1) k = 4; 2) k = -0,7; 3) k = 2/3. 951. 1) ні; 2) так; 3) ні. 952. 1) ні; […]...

  2. Функції Урок № 68 Тема. Функції Мета: виявити рівень засвоєння обов’язкових знань та вмінь з теми “Функція”, передбачених програмою з математики та ступінь сформованості навичок. Тип уроку: контроль знань та вмінь. Форма проведення: тематична контрольна робота. Хід уроку І. Перевірка домашнього завдання II. Умова тематичної контрольної роботи Варіант 1 Варіант 2 1?. Функцію задано формулою У […]...

  3. Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...

  4. Лінійна функція, її графік та властивості Розділ 2. ФУНКЦІЇ & 21. Лінійна функція, її графік та властивості Приклад 1. Маса одного цвяха 4 г, а маса порожнього ящика – 600 г. Залежність між масою т (у г) ящика із цвяхами і кількістю цвяхів у ньому, що дорівнює х (х – натуральне число), можна задати формулою: M = 4x + 600. Приклад […]...

  5. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...

  6. Лінійна функція, її графік та властивості Урок № 65 Тема. Лінійна функція, її графік та властивості Мета: ознайомити учнів із “особливими випадками” лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (див. попередній урок) […]...

  7. Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...

  8. Пряма та обернена пропорційність Математика – Алгебра Множення і ділення звичайних дробів Пряма та обернена пропорційність Дві змінні величини, відношення відповідних значень яких є сталим, називаються ­Прямо пропорційними. Це означає, що при збільшенні (зменшенні) однієї величини в декілька разів у стільки ж разів збільшується (зменшується) друга величина. Приклади прямо пропорційних величин: 1) У випадку руху з постійною швидкістю пройдена […]...

  9. Пряма пропорційність. Пропорційні величини Урок № 4 2 Тема. Пряма пропорційність. Пропорційні величини Мета: сформувати уявлення учнів про пряму пропорційну залежність величин, ознайомити із прикладами таких величин, що їх учні зустрічають у повсякденному житті та під час вивчення шкільних предметів; сформувати вміння розв’язувати задачі цього типу складанням пропорції. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього […]...

  10. Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...

  11. Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...

  12. Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...

  13. Розв’язування вправ. Самостійна робота УРОК 4 Тема. Розв’язування вправ. Самостійна робота Мета уроку: формування умінь будувати графіки функцій за до­помогою геометричних перетворень. І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування вправи № 3 (4; 5; 6), дру­гий – № 3 (7; 8; 9), третій – № 3 (18). 2. Математичний диктант. Запишіть формулою функцію, графік якої одержано в […]...

  14. Поняття про обернену функцію УРОК 17 Тема. Поняття про обернену функцію Мета уроку: формування понять: оборотна функція, обернена функція. Вивчення алгоритму знаходження форму­ли функції, оберненої до даної, властивості графіків взаємно-обернених функцій. І. Аналіз контрольної роботи II. Сприймання і усвідомлення нового матеріалу На уроках математики ви неодноразово розв’язували задачу: обчислити значення функції у = f(x) при заданому значенні х0 аргументу. […]...

  15. Пряма мова – Пряма і непряма мова УКРАЇНСЬКА МОВА. ПІДГОТОВКА ДО ЗНО СИНТАКСИС І ПУНКТУАЦІЯ Пряма і непряма мова Пряма мова – це чуже мовлення, передане дослівно, без змін: Хтось із дитям удвох бродить різдвяним садком. Каже дитятко: “Я – Бог”, трусить сніжком (І. Малкович). Пряма мова супроводжується словами автора, що вказують, кому належить пряма мова, за яких обставин вона висловлена тощо. […]...

  16. Лінійна функція, її графік і властивості 849. Лінійною функцією є: 850. Прямою пропорційністю є функції: 851. y = 6x – 5 X -3 -2 -1 0 1 2 3 У -23 -17 -11 -5 1 7 13 852. 1) y = -2x + 5 Якщо x = -4, то у = -2 • (-4) + 5 = 13. Якщо x = […]...

  17. Графік функції Урок № 63 Тема. Графік функції Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”. Хід уроку I. Організаційний момент Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці. II. Перевірка домашнього […]...

  18. Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...

  19. ЛІНІЙНА ФУНКЦІЯ РОЗДІЛ 4 ФУНКЦІЇ &17. ЛІНІЙНА ФУНКЦІЯ У дослідженні реальних процесів і явищ функції відіграють особливу роль – математичних моделей. Найбільш важливим функціям математики дають власні назви. Однією з них є лінійна функція. Розглянемо приклади, що приводять до лінійної функції. Нехай 1 кг цукерок коштує 25 грн. Тоді залежність між масою т цукерок та їх вартістю […]...

  20. Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...

  21. Синтаксичний розбір речення з прямою мовою – Пряма і непряма мова. Діалог СИНТАКСИС І ПУНКТУАЦІЯ Пряма і непряма мова. Діалог Синтаксичний розбір речення з прямою мовою Послідовність розбору 1. Указати, що дане речення є реченням із прямою мовою. 2. Виділити слова автора і пряму мову. 3. Розібрати слова автора і пряму мову як відповідні прості речення. 4. Пояснити розділові знаки. “Назбирай, Петрику, Жменю малини!”- Гойкнув Василь Услід […]...

  22. Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...

  23. Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометрич­них функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...

  24. Лінійна функція та її графік Урок № 66 Тема. Лінійна функція та її графік Мета: сформувати свідоме розуміння учнями взаємозв’язку між взаємним розташуванням графіків двох лінійних функцій та співвідношенням їх кутових коефіцієнтів; виробити вміння: за даними рівняннями лінійних функцій робити висновки щодо взаємного розташування графіків; знаходити аналітичним способом координати точки перетину графіків двох лінійних функцій. Тип уроку: застосування знань, умінь […]...

  25. Парність функції Математика – Алгебра Числові функції Парність функції Функція називається Парною, якщо: 1) ; 2) . У парних функцій протилежним значенням аргументу відповідають рівні значення функції. Графік парної функції симетричний відносно осі Oy. Функція називається Непарною, якщо: 1) ; 2) . У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції. Графік непарної функції симетричний відносно […]...

  26. ПОВТОРЕННЯ. ФУНКЦІЇ Цілі: – навчальна: узагальнити та систематизувати знання учнів про зміст основних понять теми “Функції”; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. Обладнання та наочність: […]...

  27. ЗАДАЧІ І ВПРАВИ НА ПОВТОРЕННЯ ПОВТОРЕННЯ ЗАДАЧІ І ВПРАВИ НА ПОВТОРЕННЯ Розділ 1. ВИРАЗИ І ТОТОЖНОСТІ 1. Дано числа 4 і 2. Складіть вираз, який є: 1) сумою чисел; 2) різницею чисел; 3) добутком чисел; 4) часткою чисел; 5) степенем, у якого перше число є основою; 6) степенем, у якого перше число є показником. Знайдіть значення цих виразів. 2. Знайдіть […]...

  28. Пряма мова та діалог. Тематичне тестування (тема “Пряма мова та діалог”) ВІДОМОСТІ З СИНТАКСИСУ І ПУНКТУАЦІЇ Урок № 46 Тема: Пряма мова та діалог. Тематичне тестування (тема “Пряма мова та діалог”) Мета: закріпити знання учнів про пряму мову й діалог, вміння вживати розділові знаки у реченнях з прямою мовою та текстах, що містять діалог; з’ясувати рівень знань та сформованості вмінь з теми “Пряма мова та діалог”; […]...

  29. Питання для самоконтролю – Пряма і непряма мова УКРАЇНСЬКА МОВА. ПІДГОТОВКА ДО ЗНО СИНТАКСИС І ПУНКТУАЦІЯ Пряма і непряма мова Питання для самоконтролю 1. Що називається прямою мовою? 2. Чим пряма мова відрізняється від непрямої? 3. Які розділові знаки ставляться, коли пряма мова стоїть після слів автора? 4. Які розділові знаки ставляться, якщо пряма мова стоїть перед словами автора? \ 5. Які розділові […]...

  30. Пряма і непряма мова як засоби передачі чужої мови – Пряма і непряма мова. Діалог СИНТАКСИС І ПУНКТУАЦІЯ Пряма і непряма мова. Діалог Пряма і непряма мова як засоби передачі чужої мови Для передачі чужого мовлення в тексті вживаються речення з прямою або непрямою мовою, а також прості речення з додатком, що називає тему чужого мовлення, або зі вставними словами чи реченнями, що вказують на джерело повідомлення. “Я хочу грати […]...

  31. Степенева функція УРОК 41 Тема. Степенева функція Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками. І. Перевірка домашнього завдання 1. Перевірити наявність виконаного домашнього завдання. 2. Розв’язування вправ. А) Обчислити . Відповідь: 5. Б) Спростити вираз . Відповідь: ab. В) Спростити вираз . Відповідь: 2a. II. Сприймання і усвідомлення матеріалу про степеневу функцію Степеневою […]...

  32. Послідовність розбору конструкції з прямою мовою – Пряма і непряма мова УКРАЇНСЬКА МОВА. ПІДГОТОВКА ДО ЗНО СИНТАКСИС І ПУНКТУАЦІЯ Пряма і непряма мова Послідовність розбору конструкції з прямою мовою 1. Навести аналізовану конструкцію. 2. Вказати пряму мову і слова автора, інтонаційний та змістовий зв’язки. між ними. 3. Визначити місце прямої мови щодо слів автора. 4. Пояснити розділові знаки. 5. Проаналізувати окремо пряму мову і слова автора, […]...

  33. Пряма мова Словосполучення Пряма мова Пряма мова – дослівна передача чужого висловлювання. Пряма мова утворює особливе складне речення, яке складається із двох частин: слів автора (вказівки на те, кому належить висловлювання) та власне прямої мови (чужого висловлювання): Божий чоловік положив Петрусеві на голову руку та й каже: “Добрий козак; по батькові пішов…” (П. Куліш) Слова автора можуть […]...

  34. Завдання для перевірки знань до §§ 19-21 1. 1) у = х2 + х; 3) – функції. 2. 1) у = 3х – 7; 3) у = 4 – лінійні функції. 3. 1) у = -2х + 6; k = -2; l = 6; 2) у = 7,4x; k = 7,4; l = 0. 4. у = -2х + 7; 1) х […]...

  35. Лінійна функція Розв’яжіть задачі 882. мал. 40. 883. 1) ні; 2) ні; 3) так. 884. 1) так; 2) ні; 3)так. 885. 1) ні; 2) ні; 3) так. 886. 1) ні; 2) ні; 3) так. 887. 1) ні; 2) ні; 3) так. 888. 1) 4; 2) -6; 3) 2/3. 889. 1) 3; 2) -0,5; 3) %. 890. 1) […]...

  36. Аналіз підсумкової контрольної роботи. Розв’язування цікавих задач УРОКИ № 68, 69 Тема. Аналіз підсумкової контрольної роботи. Розв’язування цікавих задач Задачі підвищеної складності 1. При яких значеннях а рівняння не має дійсних коренів? 1) х2 + 4х – а = 0; 2) (а – 1)х2 + (2а – 3)х + а = 0; 3) (а – 2)х2 – 2(а – 3)х + а […]...

  37. Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...

  38. Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...

  39. ПРЯМА, ПРОМІНЬ, ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 2. ПРЯМА, ПРОМІНЬ, ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ На малюнку 7 ви бачите лінію високовольтної електропередачі, а на малюнку 8 – автомагістраль. Вони витягнуті, як струна, і ні початку, ні кінця їх не видно. Схематично кожну з них можна зобразити прямою лінією (мал. 9). Мал. 7 Мал. 8 Мал. 9 […]...

  40. Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...

Ви зараз читаєте: ПРЯМА ПРОПОРЦІЙНІСТЬ
«
»