РІВНОМІРНИЙ РУХ МАТЕРІАЛЬНОЇ ТОЧКИ ПО КОЛУ
Розділ 2 МЕХАНІЧНИЙ РУХ
& 21. РІВНОМІРНИЙ РУХ МАТЕРІАЛЬНОЇ ТОЧКИ ПО КОЛУ
Рух тіла по колу. У природі та техніці ми часто зустрічаємося з криволінійними рухами. Одним з випадків такого руху є рух тіла по колу. Прив’яжемо до цупкої нитки якийсь невеликий тягарець, наприклад гайку, і почнемо її розкручувати, тримаючи за вільний кінець. Траєкторіями руху усіх точок тягарця будуть кола. Такий рух тіла називають рухом по колу. Якщо нитка досить довга, то радіуси кіл, які описують різні точки тягарця, мало розрізнятимуться, а їх центри практично
Рух тіла, розмірами якого у порівнянні з радіусом кола, по якому воно рухається, можна знехтувати, називають рухом матеріальної точки по колу.
Прикладами руху тіл по колу є рух кабінок колеса огляду (мал. 2.49), рух автомобіля по дузі кола при повороті (мал. 2.50), рух Землі та інших планет навколо Сонця, рух штучних супутників Землі по коловим орбітам. Як рух матеріальної точки по колу можна розглядати рух клапана (“золотника”) велосипедної камери відносно самого велосипеда й окремих частин його колеса.
Мал. 2.49
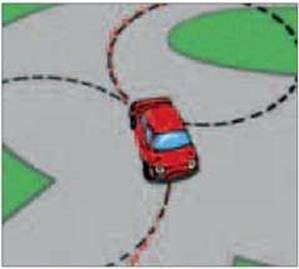
Мал. 2.50
Якщо під час руху по колу за будь-які однакові проміжки часу матеріальна точка описує дуги однакової довжини, то такий рух називають рівномірним рухом по колу. Під час рівномірного руху по колу модуль швидкості руху тіла (матеріальної точки) не змінюється, а її напрямок змінюється.
Переконатися в цьому можна, спостерігаючи процес заточування інструмента на електричному точилі чи іншому подібному приладі. Іскри – частинки розпеченого металу і самого каменя, що відриваються в різних його точках, рухаються по дотичних до кола (мал. 2.51).
Так само по дотичній до кола буде рухатися тягарець, якщо нитка, на якій його розкручують, раптом обірветься (мал. 2.52).
Мал. 2.51
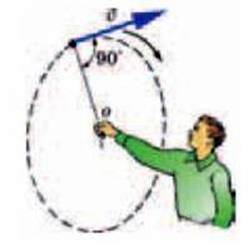
Мал. 2.52
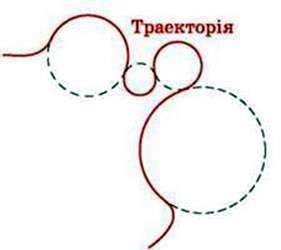
Мал. 2.53
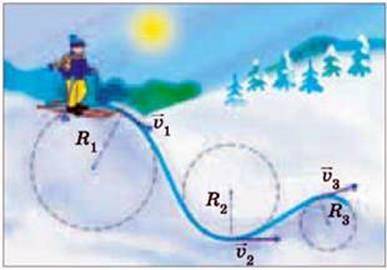
Мал. 2.54
Як правило, будь-який криволінійний рух матеріальної точки можна подати як рух по дугах кіл різного радіуса (мал. 2.53, 2.54).
Період і частота обертання. Особливістю руху по колу є те, що тіло (матеріальна точка) через деякий проміжок часу, описавши повне коло, повертається в початкове положення. У такому разі говорять: “Тіло зробило один повний оберт”. Кількість обертів, які робить тіло за той чи інший час,- одна з характеристик руху тіла по колу. Зазвичай кількість обертів позначають великою латинською літерою N.
Якщо кожен оберт тіла відбувається протягом одного й того самого проміжку часу, обертання називають періодичним.
Час, протягом якого тіло робить один повний оберт, називають періодом обертання.
Період обертання позначають літерою Т і вимірюють у секундах. Наприклад, якщо Т = 1 с, це означає, що тіло здійснює один повний оберт за одну секунду. Якщо, катаючись на велосипеді, за час t = 10 c ви зробили N= 20 повних обертів педалей, то період обертання педалей становитиме Тп =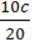 
= 0, 5 c.
Позначивши час літерою t, можна записати формулу для знаходження періоду обертання тіла:
Т = 
.
Період обертання – важлива характеристика руху планет. Наприклад, Земля робить повний оберт навколо Сонця за 1 рік (365 діб). Період обертання Землі навколо Сонця становить 365 діб.
Частота обертання. Швидкість, з якою їде ваш велосипед, залежить від кількості обертів педалей, які ви робите за одну хвилину чи одну секунду (за одиницю часу). А як знайти, скільки обертів зроблено педалями за 1 с? Для цього потрібно загальну кількість зроблених обертів поділити на час, протягом якого ви крутили педалі. Якщо 20 обертів педалей ви зробили за 10 с, г 20 об то за одну секунду ви встигли зробити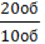 
= 2 
.
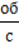Кількість обертів, які тіло робить за одиницю часу, називають частотою обертання.
Частоту обертання позначають маленькою латинською літерою n і вимірюють у обертах за секунду (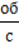). Якщо тіло робить один оберт за одну секунду, то частота його обертання 1
= 1 c-1 (CI).
Щоб визначити частоту обертання, потрібно кількість обертів, зроблених тілом, поділити на час, протягом якого вони були здійснені:
N = 
У техніці використовують й іншу одиницю – оберт за хвилину (1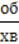 
). Зрозуміло, що за 1 хв тіло, що обертається, зробить у 60 разів більше обертів, ніж за 1 с: 60 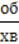= 1 .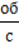
Оскільки період – це час, за який відбувається один повний оберт, а частота – кількість обертів за одиницю часу, то між ними існує просте співвідношення: Т = 
(порівняйте формули для визначення періоду і частоти).
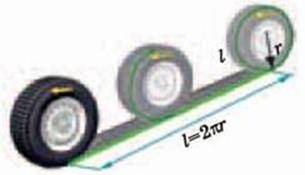
Мал. 2.55
Мал. 2.56
Мал. 2.57
Від періоду обертання коліс автомобілів, мотоциклів, велосипедів залежить швидкість їх поступального руху і пройдений ними шлях. Шлях, який проходить колесо за один оберт, дорівнює довжині його кола. Довжина протектора шини колеса, що котиться по дорозі, залежить від його радіуса і визначається за відомою формулою: l = 2r = d (мал. 2.55). Велосипед, автомобіль проїдуть тим довшу відстань, чим більше обертів зроблять їх колеса. За радіусом r або діаметром d колеса та кількістю обертів N, яке воно зробило за певний час, можна визначити пройдений колесом шлях:
S = IN = 2rN = dN.
Чим далі знаходиться точка від осі обертання, тим більший радіус і більша довжина кола, яке вона описує. Проте час, за який відбувається один повний оберт, є однаковим для усіх точок тіла.
На принципі підрахунку числа обертів коліс відомого радіуса (діаметра) працюють покажчики шляху (одометри), вмонтовані у спідометри автомобілів (мал. 2.56), велосипедів (мал. 2.57), мотоциклів. Також на цьому принципі грунтується дія курвіметрів, які використовують для визначення відстаней на місцевості (мал. 2.58) та на мапах (мал. 2.59). Радіус їх коліщат добирають так, щоб довжина їх обода становила 1 м або 1 см.
Мал. 2.58
Мал. 2.59
Період і частота обертання – важливі характеристики багатьох машин і механізмів, де використовується обертальний рух: двигунів автомобілів і літаків, електродвигунів, що приводять у рух станки, кухонні машини, вентилятори, електропотяги. Тому частота обертів завжди вказується на спеціальних табличках на двигунах, а також у технічних паспортах до них (мал. 2.60).
Рух по колу може бути рівномірним і нерівномірним. Якщо довжини дуг кіл, які описує точка тіла, що обертається, за будь-які проміжки часу однакові, таке обертання називають рівномірним.
Мал 2.60
Швидкість матеріальної точки під час руху по колу. Спостерігаючи за обертанням колеса велосипеда, ви помічали, що його спиці можна розгледіти біля осей, навіть якщо воно рухається досить швидко, а біля ободів їх розгледіти неможливо. Чому так? Пояснити це можна тим, що за однаковий час, наприклад за період обертання, різні точки на спиці колеса описують різні траєкторії і проходять різний шлях. Чим далі від осі обертання розташована точка, тим більший радіус і більша довжина кола, яке вона описує. Нехай колесо робить один оберт за 1 с. Тоді точка на його спиці, розташована на відстані r = 5 см від осі обертання, за цей час проходить шлях, що дорівнює довжині кола: s = 2r = 2 ∙ 3,14 ∙ 5 см ≈ 31 см ≈ 0,3 м. Її швидкість по колу становитиме приблизно 0, 3 
. Точка колеса на відстані R = 30 см описує коло, довжина якого у шість разів більша – приблизно 1,9 м. У стільки ж разів більшою є швидкість з якою вона рухається, – 1,9 .
Швидкість, з якою рухається точка по колу, називається лінійною швидкістю руху по колу.
Щоб знайти лінійну швидкість точки, необхідно довжину кола, яке вона описує, поділити на період обертання, або помножити на частоту обертання:
V =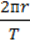
= 2пrv.
Саме лінійна швидкість протектора шини визначає швидкість автомобіля, велосипеда, мотоцикла.
Місяць – природний супутник Землі. Найближче до Землі природне космічне тіло – це Місяць. Упродовж мільйонів років він невідступно супроводжує Землю у космічному просторі, обертаючись навколо неї.
Місяць робить один оберт навколо Землі приблизно за 29,5 земних діб. Період його обертання навколо Землі такий, як і період обертання навколо власної осі. Тому Місяць завжди обернений до нас одним боком, а день і ніч на ньому тривають майже 15 земних діб. Відстань до Місяця становить приблизно 384 000 км, а його середній радіус – 1738 км.
Період обертання планет та їх супутників, зокрема Місяця, залежить від того, яке тіло ми обираємо за тіло відліку, стосовно якого спостерігаємо їх рух. Зазначений період обертання відповідає поверненню Місяця у те саме положення щодо Сонця. Якщо положення Місяця визначається відносно зірок, то період його обертання приблизно 27,3 діб. Тому в астрономії розрізняють синодичний (або сонячний) і сидеричний (або зоряний) періоди обертання. Як бачимо, й тут виявляється відносність механічного руху.
ЗАПИТАННЯ ТА ЗАВДАННЯ
1. Який рух називають обертальним? Наведіть приклади обертальних рухів.
2. Що називають періодом обертання?
3. Що називають частотою обертання?
4. Кожен з вас користувався годинником зі стрілками. Який період обертання секундної, хвилинної та годинної стрілок годинника? Яка частота їх обертання?
5. Довжина екватора Землі становить 40 000 км. Визначте швидкість (у кілометрах за годину) руху осіб і предметів, які перебувають на екваторі.
6. У табличці, закріпленій на двигуні, вказано – 2400 об/хв. Скільки обертів за секунду робить цей двигун? Який період обертання двигуна (у секундах)?
7. Мапа має масштаб, за якого 1 см на ній відповідає певній кількості кілометрів на місцевості. Який діаметр коліщати курвіметра, якщо кожен його оберт відповідає 1 см відстані на карті?
ЛАБОРАТОРНА РОБОТА № 4
Визначення періоду обертання та швидкості руху по колу
Завдання. Визначити період та частоту обертання кульки, підвішеної на нитці, під час її руху по колу. Дослідити, як залежить період (частота) від радіуса кола та довжини нитки.
Обладнання: штатив; кулька на нитці; секундомір.
Підготовка до проведення експерименту
1. На нитці довжиною приблизно 40-50 см закріпіть кульку і підвісьте її на штативі.
2. На аркуші паперу накресліть три концентричних кола, невеликих за радіусом, наприклад: 2, 4 і 6 см.
3. Відрегулюйте висоту підвісу так, щоб кулька висіла над центром кіл на висоті 1-2 см від їх площини.
4. Підготуйте таблицю для занесення результатів вимірювань:
Номер Досліду | Час усіх обертів t, c | Кількість обертів N | Період обертання Т, с | Частота обертання п, 1/с | Радіус кола R, м | Довжина нитки І, см |
1 | ||||||
2 | ||||||
3 |
Проведення експерименту
1. Відведіть кульку від положення рівноваги так, щоб вона опинилася над одним із кіл, і штовхніть її, надавши швидкість, направлену по дотичній до кола. Підберіть силу поштовху такою, щоб радіус траєкторії руху кульки був близьким до радіуса відповідного кола.
2. Виміряйте час, за який кулька робить певну кількість обертів (наприклад, 10), визначте період і частоту обертання кульки.
3. Виміряйте період та частоту обертання під час руху кульки по колах інших радіусів.
4. Вкоротіть довжину нитки, наприклад у 2 та 4 рази, повторіть вимірювання часу та визначте періоди і частоти обертання кульки за цих умов. Занесіть дані до таблиці.
5. Зробіть висновки щодо залежності періоду обертання. Визначте лінійні швидкості обертання, якщо радіуси кіл різні.
(1 votes, average: 5.00 out of 5)
Loading...