Головна ⇒ 📌Формули й таблиці ⇒ Рівносторонній трикутник – ТРИКУТНИКИ
Рівносторонній трикутник – ТРИКУТНИКИ
Формули й таблиці
МАТЕМАТИКА
ТРИКУТНИКИ
Рівносторонній трикутник
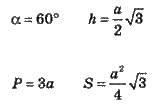
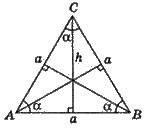
Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр.
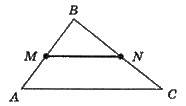
Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника.
Теорема: 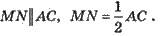
Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника.
Теорема: 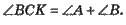
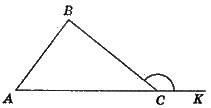
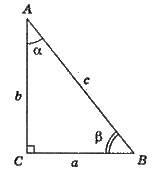
Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с 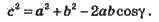
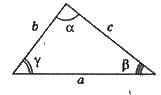
Теорема синусів: у будь-якому трикутнику 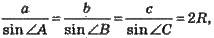
Де R – радіус описаного навколо трикутника кола.
Співвідношення між сторонами кутами у прямокутному трикутнику.
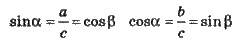
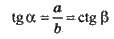
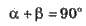
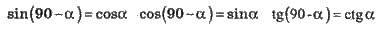
Related posts:
- Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Трикутник загального виду – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник загального виду R – радіус описаного кола R – радіус вписаного кола Формула Герона:...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Прямокутний трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Прямокутний трикутник Теорема Піфагора:...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...
- Розв’язування задач на застосування теореми синусів УРОК № 8 Тема. Розв’язування задач на застосування теореми синусів Мета уроку: формування вмінь учнів застосовувати теорему синусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], посібник [14]. Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв’язування задач. Хід уроку І. Перевірка домашнього завдання 1. […]...
- Формули косокутних трикутників 10. Додатки 36. Формули косокутних трикутників Теорема синусів: Теорема косинусів: Теорема тангенсів:...
- Теорема синусів УРОК № 7 Тема. Теорема синусів Мета уроку: вивчення теореми синусів. Формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: формулюють теорему синусів та доводять її. Хід уроку І. Перевірка домашнього завдання Перевірити правильність виконання домашніх […]...
- РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...
- Застосування розв’язування трикутників у прикладних задачах УРОК № 11 Тема. Застосування розв’язування трикутників у прикладних задачах Мета уроку: формування вмінь учнів застосовувати знання розв’язування трикутників до розв’язування прикладних задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], таблиця 2, посібник [14]. Вимоги до рівня підготовки учнів: розв’язують трикутники. Застосовують алгоритми розв’язування трикутників до розв’язування прикладних […]...
- Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...
- Формули радіусів вписаних і описаних кіл правильних многокутників УРОК № 18 Тема. Формули радіусів вписаних і описаних кіл правильних многокутників Мета уроку: Виведення формул для радіусів вписаних і описаних кіл правильного многокутника. Формування вмінь застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 5, 6. Вимоги до рівня підготовки учнів: записують і пояснюють формули радіусів вписаного та описаного кіл […]...
- Трикутник і його види Урок 40 Тема. Трикутник і його види Мета: подальше закріплення знань учнями класифікації трикутників, доповнення їх алгоритмами побудови трикутників за двома сторонами і кутом між ними та за стороною і прилеглими кутами; формування вмінь розв’язування задач на побудову і вдосконалення вмінь розв’язувати задачі на обчислення периметрів прямокутника, квадрата і трикутника. Тип уроку: застосування знань, умінь, […]...
- Розв’язання трикутників Геометрія Розв’язування трикутників Розв’язування трикутників Розв’язування трикутників полягає у знаходженні невідомих сторін і кутів трикутника за відомими його сторонами та кутами. Результати в таких задачах наближені, тому що для більшості значень кутів наближеними є значення їх синуса і косинуса. Задача 1. Розв’язати трикутник за стороною й двома прилеглими кутами. На рисунку в трикутнику дано: a; […]...
- Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...
- Основні задачі на розв’язування трикутників УРОК № 10 Тема. Основні задачі на розв’язування трикутників Мета уроку: ознайомити учнів з основними задачами розв’язування трикутників. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: описують основні випадки розв’язування трикутників та алгоритми їх розв’язування. Хід уроку І. Перевірка домашнього завдання Фронтальне опитування 1) […]...
- ПРЯМОКУТНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 16. ПРЯМОКУТНИЙ ТРИКУТНИК Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°. Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають […]...