Рівняння кола
УРОК № 26
Тема. Рівняння кола
Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13].
Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола.
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час їх виконання.
II.
III. Сприйняття й усвідомлення нового матеріалу
В алгебрі ми зустрічалися з різними рівняннями і будували їх графіки.
Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними х і у, яке задовольняють координати будь-якої точки фігури, і навпаки: будь-які два числа, які задовольняють це рівняння, є координатами деякої точки цієї фігури.
Яке ж рівняння має коло?
Для того щоб скласти рівняння кола, згадаємо його властивість, що міститься в означенні кола: усі точки кола розміщені в одній площині з його центром і однаково від
Нехай центр кола М(а; b), а радіус кола R (рис. 140).
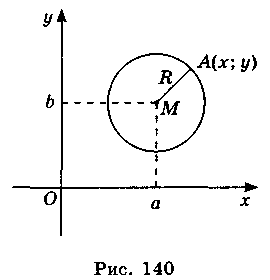
Позначимо на колі будь-яку точку А (х; у). Відстань від точки М до точки А дорівнює R, тобто AM = R, але за формулою відстані між двома точками маємо АМ2 = (х – а)2 + (y – b)2, або (x – a)2 + (y – b)2 = R2. (1)
Координати будь-якої точки цього кола задовольняють рівняння (1). Правильно і те, що будь-яка точка, координати якої задовольняють рівняння (1), належить колу.
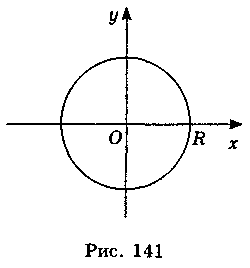
Отже, (x – a)2 + (y – b)2 = R2 – рівняння кола. Якщо центр кола (рис. 141) лежить у початку координат, то воно має рівняння х2 + у2 = R2.
Розглянемо рівняння (1), у якому х і у – змінні координати точок кола, а числа а і b – відповідно абсциса і ордината центра, R – радіус кола. Отже, щоб записати рівняння кола, треба запам’ятати цю формулу і знати координати центра і радіус.
Наприклад, нехай M(-1; 2), a R = 2, тоді рівняння кола (x + 1)2 + (y – 2)2 = 4.
Виконання вправ
1) Які з точок: А(1; 2), В(3; 4), С(-4; 3), D(0; 5), F(5; -1) – лежать на колі, рівняння якого х2 + у2 = 25? 2) Запишіть рівняння кола радіуса 1, а координати центра:
А) (1; 1);
Б) (-1; 1);
В) (1; -1);
Г) (-1; -1)
3) Укажіть координати центра і радіус кола, яке задане рівнянням:
A) (x – 1)2 + y2 = 9;
Б) (x + 1)2 + (у + 3)2 = 1;
В) x2 + (y + 1)2 = 2;
Г) (x + 1)2 + (y + 2)2 = 7.
4) Знайдіть на колі х2 + у2 = 100 точки:
А) з абсцисою 6;
Б) з ординатою 8.
IV. Закріплення й усвідомлення нового матеріалу
Розв’язування задач
1. Дано точки А(2; 1), В(-2; 5). Складіть рівняння кола, діаметром якого є відрізок АВ. 2. Дано точки А(-1; -1) і С(-4; 3). Складіть рівняння кола:
А) з центром у точці А і яке проходить через точку С;
Б) з центром у точці С і яке проходить через точку А.
3. Знайдіть на осі Ох центр кола, яке проходить через точку А(1; 4) і має радіус 5. 4. Складіть рівняння кола з центром (1; 2), яке дотикається до осі Ох. 5. Складіть рівняння кола з центром (-3; -4), яке проходить через початок координат. 6. Доведіть, що відрізок АВ, кінці якого А(2; -5) і В(5; -2) є хордою кола (х – 5)2 +(у + 5)2 = 9. 7. Чи перетинає коло (х + 4)2 + (у – 1)2 = 20 вісь Оу? Якщо перетинає, то в яких точках?
V. Домашнє завдання
Вивчити рівняння кола та розв’язати задачі.
1. Коло задане рівнянням (х – 1)2 + (у + 3)2 =10. Чи проходить це коло через початок координат? 2. Чи перетинає коло (х – 3)2 + (у + 5)2 = 26 вісь Ох? Якщо перетинає, то знайдіть точки перетину з віссю Ох. 3. Знайдіть рівняння кола, діаметром якого є відрізок АВ, якщо А(8; 5), В(2; -3).
VI. Підбиття підсумків уроку
Завдання класу
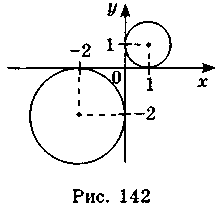
1. Запишіть рівняння кола. 2. Знайдіть координати центра і довжини радіусів кіл, зображених на рис. 142. Запишіть рівняння цих кіл.