Рівняння. Кути. Прямокутник. Трикутник і його види
УРОК 41
Тема. Рівняння. Кути. Прямокутник. Трикутник і його види
Мета: підготовити учнів до тематичної контрольної роботи.
Тип уроку: повторення і систематизація знань.
Хід уроку
I. Актуалізація опорних знань
Усні вправи
1. Знайти корінь рівняння:
1) х + 15 = 29;
2) 30 – х = 17;
3) х – 12 = 19;
4) 12 + х = 6.
2. Назвати всі кути на рис. 70 і знайти їх величини, якщо:
Промінь NP – бісектриса кута MNK;
Промінь NS – бісектриса кута PNK.
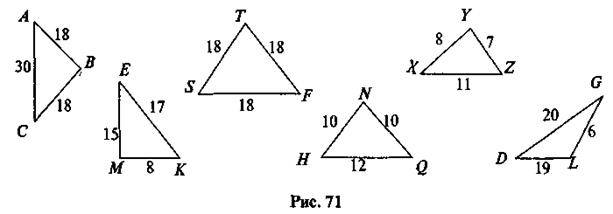
3. На рис. 71 зображено трикутники, довжини сторін яких
1) рівностороннього трикутника;
2) тупокутного рівнобедреного трикутника;
3) прямокутного рівностороннього трикутника;
4) гострокутного нерівнобедреного трикутника.
II. Повторення і систематизація знань, узагальнення вмінь
@ Оскільки основна мета уроку – підготовка учнів до тематичної контрольної роботи., то бажано організувати роботу учнів за трьома основними напрямами:
1) рівняння;
2) кути;
3) трикутники.
Також доцільно задачі на повторення і систематизацію матеріалу формувати в тріади (по 3 задачі схожого
1. Рівняння
Розв’язати рівняння:
1) а) х + 29 = 53; б) 150 – х = 76.
2) а) (26 + х) – 42 = 36; б) 55 – (х – 13) = 21.
3) Яке число треба підставити замість а, щоб коренем рівняння (а – х) + 4 = 15 було число 3? (№ 290, б).
2. Кути
1) Побудувати кут MNK, величина якого дорівнює 56°. Провести довільний промінь NA між сторонами кута MNK. Записати назви кутів, що утворились. Виміряти величини кутів і знайти їх суму. Чому вона дорівнює?
2) З вершини розгорнутого кута ABC проведено 2 промені BD і ВК так, що 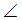 ABK = 152°,
ABK = 152°, 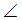 CBD = 143°. Обчислити
CBD = 143°. Обчислити 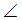 DBK.
DBK.
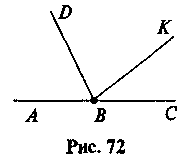
3) На рис. 72 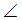 ABK = 130°. Знайти кут між бісектрисами кутів АВК і СВК.
ABK = 130°. Знайти кут між бісектрисами кутів АВК і СВК.
3. Трикутники
Дано: ABC. Знайти:
1) Його периметр, якщо АВ = 5 см; ВС = 5 см; АС = 6 см.
2) Сторону АВ, якщо периметр 20 см; ВС = 5 см; АС = 6 см.
3) Його периметр, якщо АВ = 13 см, ВС – у 2 рази довша за АВ, АС на 5 см коротша від ВС.
III. Домашнє завдання
І варіант
У робочих зошитах виконати “Тематичне оцінювання № 3” (с. 35).
II варіант
Повторити пп. 10-14, № 392; 371; 365; 390.