Головна ⇒ 📌Плани-конспекти уроків по фізиці ⇒ Рівняння стану ідеального газу

Рівняння стану ідеального газу

2-й семестр

МОЛЕКУЛЯРНА ФІЗИКА Й ТЕРМОДИНАМІКА

1. Властивості газів, рідин, твердих тіл

Урок 8/79

Тема. Рівняння стану ідеального газу

Мета уроку: одержати залежність між макроскопічними параметрами (р, V, Т), що характеризують стан газу

Тип уроку: вивчення нового матеріалу

План уроку

Контроль знань	4 хв.	1. Основне рівняння молекулярно-кінетичної теорії ідеального газу. 2. Зв’язок тиску з середньою кінетичною енергією молекул.
Демонстрації	3 хв.	Залежність між об’ємом, тиском і температурою газу.
Вивчення нового матеріалу	26 хв.	1. Співвідношення Клапейрона. 2. Закон Авогадро. 3. Рівняння Менделєєва-Клапейрона.
Закріплення вивченого матеріалу	12 хв.	1. Тренуємося розв’язувати задачі. 2. Контрольні запитання.

ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Співвідношення Клапейрона

Величинами, що визначають стан газу, є: тиск р, під яким знаходиться газ, його температура Т і об’єм V. їх називають параметрами стану. Перераховані три величини не

є незалежними. Кожна з них є функцією двох інших. Рівняння, що зв’язує всі три параметри – тиск, об’єм і температуру газу для даної його маси,- називається рівнянням стану і може бути в загальному вигляді записано так:

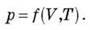
Це означає, що стан газу визначається тільки двома параметрами (наприклад, тиском і об’ємом, тиском і температурою або об’ємом і температурою), третій параметр, однозначно, визначається двома іншими. У першій половині 19-го століття французький фізик Клапейрон вивів співвідношення, що пов’язує ці три параметри – рівняння Клапейрона (рівняння стану для даної маси газу).

Для даної маси газу добуток тиску газу на його об’єм, поділено на абсолютну температуру газу, є величина постійна:

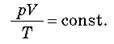
Якщо газ переводять зі стану 1 в стан 2, то параметри, які характеризують газ у кожному із станів, пов’язані виразом:

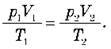
Використовуючи рівняння Клапейрона, можна довести, що всі три закони для ізопроцесів є приватними випадками цього рівняння. Дійсно, при р = const отримуємо, що V/T = const; при V = const отримуємо, що P/T = const; а при Т = const отримуємо – pV = const.

2. Закон Авогадро

Щоб переконатися в тому, що значення виразу pV/Т не завжди є постійним, наберіть повітря в щоки: одночасно збільшиться і тиск, і об’єм повітря в роті, а температура повітря залишиться практично незмінною (рівною температурі тіла). Отже, значення виразу pV/Т збільшилося. Причина в тому, що збільшилося число молекул газу.

Коли тиск і температура є постійними, об’єм газу пропорційний числу молекул N, тому значення виразу pV/Т пропорційне числу молекул N. Але чи однаковий коефіцієнт пропорційності для різних газів? Відповідь на це запитання дає закон, який був встановлений Авогадро:

O при однакових температурі й тискові в рівних об’ємах різних газів міститься однакове число молекул.

Це означає, що pV/T = kN з одним і тим же коефіцієнтом пропорційності k для всіх газів. Цей коефіцієнт називають постійною Больцмана, на честь австрійського фізика, одного з творців молекулярно-кінетичної теорії.

Вимірювання показали, що k = 1,38-10-23 Дж/К.

З рівняння pV/T = kN випливає, що тиск газу можна дуже просто виразити через концентрацію газу n = N/V і його абсолютну температуру. Ми отримаємо: р = (N/V)kT = nkT.

3. Рівняння Менделєєва-Клапейрона

Ми вже знаємо, що число молекул N пов’язане з масою речовини m і його молярною масою співвідношенням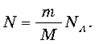

Підставляючи цей вираз у співвідношення pV/T = kN, отримуємо:

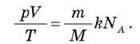
Добуток kNA позначається R і називається універсальною незмінною: R = kNA. Вимірювання показали, що R = 8,31 Дж/(моль-К). Використовуючи цю постійну, отримуємо рівняння Менделєєва-Клапейрона:

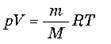Це рівняння було виведено російським ученим Д. І. Менделєєвим у другій половині 19-го століття.

Контрольні запитання

1. Що ви розумієте під параметрами стану?

2. Які параметри характеризують стан газу? Чи пов’язані вони між собою? Наведіть приклади.

3. Яке співвідношення між тиском, об’ємом і температурою для даної маси газу? Як називають це співвідношення?

4. Яка форма рівняння стану містить більше інформації: рівняння Клапейрона чи Менделєєва – Клапейрона?

5. Чому газова постійна R називається універсальною?

ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ

1). Тренуємося розв’язувати задачі

1. Визначте густину водню? за температури 127 °С і тиску 830 кПа.

Розв’язок

Скориставшись рівнянням Менделєєва-Клапейрона 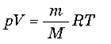І співвідношенням? = m/V, отримуємо:

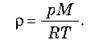
Тут

Перевіримо одиниці величин:

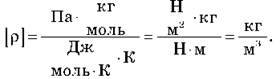
Підставимо числові значення:

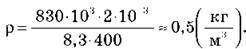
2. Чи змінюється тиск газу, розміщеного в непрохідній еластичній оболонці, якщо під час нагрівання газу від 250 К до 500 К його об’єм зріс в 1,5 рази?

3. Після підвищення температури на 9 К тиск газу в закритому балоні збільшився на 3 %. Якою була початкова температура?

4. У закритій посудині об’ємом 1 л міститься кисень масою 12 кг. Знайдіть його тиск за температури 20 °С.

2). Контрольні питання

1. Як пов’язані постійна Больцмана, постійна Авогадро й універсальна газова постійна?

2. Під час переходу визначеної маси газу з одного стану в інший його тиск зменшується, а температура збільшується. Як змінюється його об’єм?

3. Газ зменшувався в обсязі за Т = const і р = const. Як це могло бути? Чи можна цей процес зміни стану газу описати рівнянням ?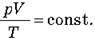

Що ми дізнаємося на уроці

– Рівняння Клапейрона: для даної маси газу добуток тиску газу на його об’єм, поділено на абсолютну температуру газу, є величина постійна:

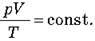
– Закон Авогадро: за однакових температури й тискові в рівних об’ємах різних газів міститься однакове число молекул.

– Тиск газу можна виразити за рахунок концентрації газу і його абсолютної температури: p = nkT.

– Модель реального газу, у якій нехтують розмірами молекул газу та їх взаємодією між зіткненнями, називають ідеальним газом.

– Рівняння Менделєєва – Клапейрона:

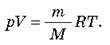
Домашнє завдання

1. Конспект.

2. Розв’яжіть задачі:

P1): 1. Під час виготовлення ламп розжарювання їх балони заповнюють азотом під тиском, значно меншим за атмосферний. Чому?

2. У циліндрі під поршнем знаходиться певна маса ідеального газу. Його об’єм збільшився в 3 рази, а абсолютну температуру зменшили в 3 рази. У скільки разів змінився тиск газу?

3. У скільки разів змінився тиск ідеального газу в герметично закритому посуді, якщо його об’єм збільшили в 4 рази, а абсолютну температуру збільшили в 2 рази?

4. Газ за температури 37 °С із тиском 1,5 МПа має об’єм 10 л. Який об’єм цієї маси газу за нормальних умов?

Р2): 1. У паровому котлі об’ємом 2 м3 знаходиться водяна пара з температурою 200 °С і з тиском 1 МПа. Яка маса цієї пари?

2. Яка маса повітря, що займає об’єм 150 л за температури 288 Кіз тиском 150 кПа?

3. Як зміниться маса повітря в кімнаті, якщо в результаті несправності опалювальної системи температура в кімнаті понизиться від 20 до 7 С°? Об’єм кімнати 60 м3.

4. Яка кількість речовини в газі, якщо за температури -13 °С і з тиском 500 кПа об’єм газу дорівнює 30 л?

Р3): 1. У скільки разів густина вуглекислого газу відрізняється від густини азоту, якщо гази знаходяться в однакових умовах?

2. Об’єм газу зменшили в 1,5 рази, у результаті чого абсолютна температура збільшилася на 20 %, а тиск – на 320 кПа. Яким був початковий тиск газу?

3. Тиск газу під поршнем збільшився в 2 рази, об’єм зменшився в 3 рази, а абсолютна температура зменшилася на 20 %. Чи змінилася маса газу під поршнем? Якщо так, то на скільки відсотків?

4. У балон об’ємом 8 л налили 10 г води. Потім балон герметично закрили й нагріли від 20 °С до 180. Вся вода випарувалася. Який тиск встановився всередині балона?