Рівняння х2 = а. Основна тотожність квадратного кореня
Урок № 36
Тема. Рівняння х2 = а. Основна тотожність квадратного кореня
Мета: повторити та узагальнити знання учнів щодо способу розв’язання рівняння виду х2 = а (записати алгоритм розв’язання рівняння із використанням знань учнів про арифметичний квадратний корінь з невід’ємного числа); використовуючи означення арифметичного квадратного кореня з невід’ємного числа, сформулювати основну тотожність для квадратного кореня; формувати вміння з використанням записаного алгоритму розв’язувати рівняння виду х2 = а, а також рівняння,
Тин уроку: повторення та узагальнення знань, застосування знань та вмінь.
Наочність та обладнання: опорний конспект “Квадратний корінь та його властивості”.
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
В учнів, які потребують додаткової педагогічної уваги, вчитель перевіряє виконання домашнього завдання, зібравши зошити на перевірку.
Усі учні можуть
III. Формулювання мети і завдань уроку
Для встановлення мети уроку достатньо пригадати разом з учнями, які поняття було вивчено на попередніх уроках цього розділу, та спробувати встановити логіку вивчення матеріалу: від уявлення про кількість коренів рівняння х2 = а (на основі уявлення про графік функції у = х2 та можливості його застосування для розв’язування рівнянь з однією змінною графічним способом) – до уявлення про дію над невід’ємними числами, обернену до піднесення до 2-го степеня (добування квадратного кореня з невід’ємного числа). Серед інших питань, які можуть виникнути під час розгляду цього логічного ланцюжка, передбачаємо такі:
– як знайти корені рівняння х2 = а, використовуючи дію добування квадратного кореня з числа;
– як ще можна використати означення арифметичного квадратного кореня з числа?
Відшукання відповіді на ці питання і становитиме мету уроку.
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: найбільш вживані значення квадратів раціональних чисел; добування коренів з раціональних чисел; графічні уявлення про кількість розв’язків рівняння х2 = а; основна властивість степеня з цілим показником та її наслідків (зокрема властивості щодо піднесення до степеня добутку), а також властивість парного степеня від’ємного числа.
Виконання усних вправ
1. Визначте сторони квадрата, площа якого дорівнює: 36 см2; 0,81 дм2; 1 м2; 900 мм2?
2. Обчисліть АКК із чисел: 4; 9; 0,25; 0,81; 0,64; 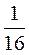 ;
; 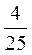 ;
; 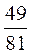 ; 3
; 3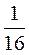 .
.
3. Скільки спільних точок має графік функції у = х2 із прямою: а) у = 4; б) у = 0,9; в) у = 0; г) у = -2; д) y = 3?
V. Застосування знань
План вивчення нового матеріалу
1. Доведення того, то при а > 0 корені рівняння х2 = а х1 і х2 дорівнюють відповідно 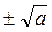 .
.
2. Загальна схема розв’язання рівняння х2 = а.
3. Формулювання та доведення основної тотожності для квадратного кореня.
@ Традиційно уявлення про існування та спосіб знаходження коренів рівняння х2 = а формується у процесі роботи з графіками функцій у = а (а – будь-яке число) та у = х2, при цьому спочатку повторюються загальні уявлення про можливу кількість коренів (див. урок 33), а вже потім здійснюється перехід до точного знаходження цих коренів, якщо вони існують. Саме по собі доведення твердження, що при а > 0 коренями рівняння х2 = а є числа 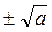 , дають лише можливість записати розв’язки рівняння. Щоб усвідомити, що при а > 0 корені рівняння х2 = а, по-перше, існуватимуть і, по-друге, завжди будуть протилежними числами, слід знову звернутись до графічних образів і на них продемонструвати справедливість цих тверджень. Після констатації цього факту доречно хоча б на рівні ознайомлення показати учням, що корені рівняння (тобто вирази виду
, дають лише можливість записати розв’язки рівняння. Щоб усвідомити, що при а > 0 корені рівняння х2 = а, по-перше, існуватимуть і, по-друге, завжди будуть протилежними числами, слід знову звернутись до графічних образів і на них продемонструвати справедливість цих тверджень. Після констатації цього факту доречно хоча б на рівні ознайомлення показати учням, що корені рівняння (тобто вирази виду 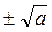 при а > 0) можуть бути не тільки раціональними (тобто створюється певна мотивація діяльності на наступний урок).
при а > 0) можуть бути не тільки раціональними (тобто створюється певна мотивація діяльності на наступний урок).
Після вивчення питання про застосування означення арифметичного квадратного кореня з невід’ємного числа для розв’язування рівняння х2 = а вивчається питання про застосування цього самого означення для перетворення виразу виду 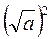 (при a? 0). Доведення цієї тотожності не повинно викликати в учнів труднощів (бо здійснюється цілком на основі означення арифметичного квадратного кореня з числа), але застосування цієї властивості разом із властивістю степеня про піднесення до степеня добутку зазвичай викликає певні труднощі в учнів. Тому після формулювання та доведення основної тотожності для арифметичного квадратного кореня слід розглянути (розібрати та записати розв’язання) кілька прикладів відповідного змісту.
(при a? 0). Доведення цієї тотожності не повинно викликати в учнів труднощів (бо здійснюється цілком на основі означення арифметичного квадратного кореня з числа), але застосування цієї властивості разом із властивістю степеня про піднесення до степеня добутку зазвичай викликає певні труднощі в учнів. Тому після формулювання та доведення основної тотожності для арифметичного квадратного кореня слід розглянути (розібрати та записати розв’язання) кілька прикладів відповідного змісту.
VI. Формування вмінь
Виконання усних вправ
1. Скільки коренів мають рівняння: х2 = 9; х2 = -9; х2 = 3; х2 = 0; х2 – 31 = 0; х2 = – 31?
2. Із рівнянь виберіть ті, які мають два протилежних:
а) раціональних корені;
Б) ірраціональних корені:
Х2 = 16; х2 – 7 = 0; х2 + 3= 0; х2 – 0,25 = 0; 0,6 – х2 = 0; – х2 – 5 = 0.
3. Знайдіть корені рівнянь: х2 = 16; у2 = 0,81; z2 = -4; m2 = 5; n2 = 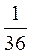 ; d2 = n
; d2 = n
Виконання письмових вправ
Для досягнення основної мети уроку письмово слід розв’язати вправи такого змісту:
1. Визначення, чи має рівняння корені, якщо має, то скільки.
1) Наведіть приклад рівняння вигляду х2 = а, яке:
А) має два раціональні корені;
Б) має два ірраціональні корені;
В) не має коренів.
2) Чи має корені рівняння:
А) х2 = 81; б) х2 = 18; в) х2 = 0; г) х2 = -25?
2. Розв’язування рівнянь виду х2 = а аналітично і графічно.
1) Розв’яжіть рівняння: а) х2 = 121; б) х2 = 0,16; в) х2 = 5; г) х2 = 0,3; д) х2 = 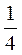 ; є) х2 =
; є) х2 = 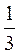 ; ж) х2 = -1; з) х2 = 1,44.
; ж) х2 = -1; з) х2 = 1,44.
2) Розв’яжіть рівняння:
А) 3х2 = 48; б) х2 + 8 = 57; в) 44 – х2 = 8; г) -2х2 = 18; д) -0,4х2 = -8; є) 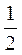 Х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
Х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
3) Розв’яжіть рівняння за допомогою графіка функції у = х2, знайдіть наближенні значення його коренів: а) х2 = 3; б) х2 = 5; в) х2 = 4,5; г) х2 = 8,5.
3. Розв’язування рівнянь, що зводяться до виду х2 = а.
1) Розв’яжіть рівняння: а) 2(х2 – 3) + 3(2х2 + 1) = 5; б) (2х – 5)2 + (2х + 5)2 = 62; в) 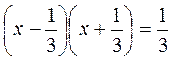 ; г) (5х + 1)2 – 2 = 10х.
; г) (5х + 1)2 – 2 = 10х.
2) Розв’яжіть рівняння: а) (х – 3)2 = 25; б) (х + 4)2 = 9; в) (х – 6)2 = 7; г) (х + 2)2 = 6.
4. Розв’язування рівняння х2 = а з параметром.
5. Знаходження значень виразів вигляду 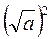 та
та 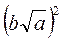 , де a? 0.
, де a? 0.
1) Знайдіть значення виразу: а) 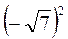 ; б)
; б) 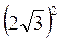 ; в)
; в) 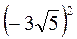 .
.
2) Знайдіть значення виразу: а) 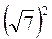 ; б)
; б) 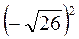 ; в)
; в) 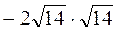 ; г)
; г) 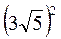 ; д) 0,5
; д) 0,5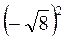 ; є)
; є) 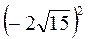 ; ж)
; ж) 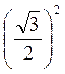 ; з)
; з) 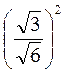 .
.
6. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Знайдіть значення виразу:
А) 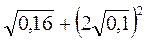 ; б)
; б) 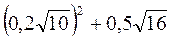 ; в)
; в) 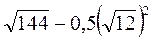 ; г)
; г) 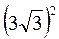 +
+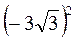 ; д)
; д) 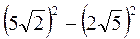 ; с)
; с) 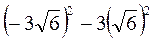 .
.
2) При яких значеннях а і b має зміст вираз: а) 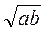 ; б)
; б) 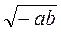 ; в)
; в) 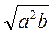 ; г)
; г) 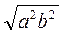 ; д)
; д) 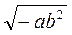 ?
?
3) Яке з даних чисел слід вилучити: 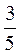 ; 1,9;
; 1,9; 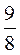 ; 1,3;
; 1,3; 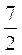 ;
; 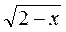 ?
?
7. На повторення: розв’язати рівняння 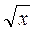 = а.
= а.
1) Розв’яжіть рівняння:
А) 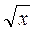 = 8; б)
= 8; б) 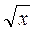 = 1; в)
= 1; в) 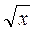 = – 4; г)
= – 4; г) 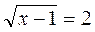 ; д)
; д) 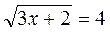 ; є)
; є) 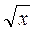 + 9 = 7; ж)
+ 9 = 7; ж) 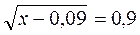 з)
з) 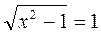 ; и)
; и) 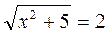 .
.
2) Розв’яжіть рівняння: а) 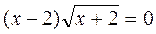 ; б)
; б) 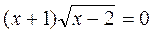 ; в)
; в) 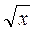 +
+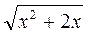 = 0; г)
= 0; г) 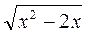 +
+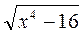 = 0.
= 0.
@ Основний зміст письмових вправ складають вправи на формування вмінь застосовувати схему розв’язання рівняння х2 = а та рівнянь, що зводяться до такого виду шляхом тотожних перетворень або заміною змінних (можна в неявному вигляді), а також вправи на закріплення знання та застосування основної властивості для квадратного кореня (при цьому на розв’язування рівнянь робиться більший акцент). Після відпрацювання умінь безпомилково застосовувати схему розв’язання рівнянь х2 = а в ситуаціях різного рівня складності доречно виконати кілька вправ на розв’язування рівнянь виду 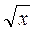 = а (вивчених на попередньому уроці), після чого зробити порівняльний аналіз схем розв’язання цих видів рівнянь (досвід показує, що учні часто-густо плутають ці схеми).
= а (вивчених на попередньому уроці), після чого зробити порівняльний аналіз схем розв’язання цих видів рівнянь (досвід показує, що учні часто-густо плутають ці схеми).
І наостанок, у разі успішного опанування питання про розв’язання рівняння х2 = а, можна запропонувати до уваги учнів найпростіші рівняння виду х2 = а з параметром.
VII. Підсумки уроку
В якому з випадків правильно розв’язано рівняння?
А) х2 – 5 = 0, -5 < 0 коренів немає. | Б) х2 – 5 = 0, х2 = 5, х = | В) х2 – 5 = 0, х2 = 5, х = |
Відповідь. Коренів немає | Відповідь. | Відповідь. |
VIII. Домашнє завдання
1. Вивчити теоретичний матеріал уроку (див. конспект).
2. Розв’язати завдання таких видів, як і в класній роботі.
3. Повторити: властивості степеня з натуральним показником (див. 7 клас), виконати вправи на застосування цих властивостей.
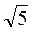 .
. .
.