РІЗНИЦЯ КВАДРАТІВ
РОЗДІЛ 3 МНОГОЧЛЕНИ
&12. РІЗНИЦЯ КВАДРАТІВ
Ви вже знаєте, що таке формули скороченого множення, і вмієте користуватися формулами квадрата суми двох одночленів і квадрата різниці двох одночленів. Ще одну формулу дістанемо, довівши наступну теорему.
Запам’ятайте!
Теорема (про добуток суми і різниці двох одночленів).
Добуток суми і різниці двох одночленів дорівнює різниці їх квадратів:
(а + b)(а – b) = а2 – b2.
Д а н о: одночлени а і b.
Д о в е с т и: (а + b)(a – b) = а2 – b2.
Доведення. Перетворимо вираз у лівій частині
(а + b) (а – b) =
= а2 + ab – ab – b2 =
= а2 – b2.
Отже, a2 – b2 – а2 – b2.
Звідси (а + b)(a – b) = а2 – b2, що і вимагалося довести.
Цю формулу також відносять до формул скороченого множення.
Оскільки доведена рівність є тотожністю, то її можна застосовувати і в зворотному порядку:
А2 – b2 – (a + b)(а – b).
Ця тотожність називається формулою різниці квадратів. Вона дозволяє заміняти різницю квадратів двох одночленів добутком їх суми і різниці.
Зверніть увагу:
– різниця квадратів двох одночленів дорівнює добутку
– квадрат різниці двох одночленів дорівнює добутку цієї різниці на себе;
– квадрат суми двох одночленів дорівнює добутку цієї суми на себе.
? Чи можна застосовувати формулу різниці квадратів не лише до найпростіших одночленів? Так.
Задача 1. Подайте у вигляді добутку двочлен 9х6у2 – 25.
Розв’язання. Перший член даного двочлена містить
– змінні х і у у парних степенях, а його коефіцієнт 9 = З2. Отже,
– цей одночлен можна подати як квадрат іншого одночлена:
9х6у2 = (3х3y)2. Число 25 є квадратом числа 5. Звідси випливає, що даний двочлен можна подати як різницю квадратів і застосувати відповідну формулу скороченого множення:
9х6y2 – 25 =
= (3х3у)2 – 52=
= (3х3у + 5)(3х3у – 5).
Задача 2. Знайдіть значення виразу 272 – 232.
Розв’язання. Застосуємо відповідну формулу скороченого множення:
272 – 232 = (27 + 23) ∙ (27 – 23) = 50 ∙ 4 = 200.
Отже, 272 – 232= 200.
Зверніть увагу:
Формулу різниці квадратів можна застосовувати до будь-яких цілих виразів.
Дізнайтеся більше
1. У вас могло виникнути запитання, чи можна подати як добуток різницю n-х степенів двох одночленів. Виявляється, що так: an – bn = (a – b)(an-1 + an-2b + аn-3 b2+…+a2bn-3 + abn-2 + bn-1). Користуючись цією формулою, можна подати як добуток, наприклад, такий вираз:
А5 – b5 = (а – b)(а4 + a3b + а2b2 + ab3 + b4).
2. Степанець Олександр Іванович (1942- 2007) – відомий український математик.
Народився в селі Комарівка на Чернігівщині в родині сільського вчителя. У 1960-1965 навчався на механіко-математичному факультеті Київського державного університету імені Тараса Шевченка. У 1969 захистив кандидатську дисертацію, а в 1974 – докторську. З 1990 був завідувачем відділу теорії функцій Інституту математики НАН України, а 1996 обійняв посаду заступника директора Інституту математики НАН України. У 1997 О. І. Степанця було обрано членом-кореспондентом НАН України. Олександр Іванович був головою видавничої ради Інституту математики НАН України, відповідальним редактором збірників праць Інституту математики НАН України з теорії наближення

Функцій, членом редакційних колегій “Українського математичного журналу” та “Українського математичного вісника”. У його науковому доробку – 200 наукових праць, зокрема 7 монографій. Він підготував 32 кандидатів та 6 докторів наук.
О. І. Степанець – лауреат Республіканської премії ім. М. Островського (1974), премії ім. М. В. Остроградського НАН України (2000) та премії ім. М. М. Крилова НАН України (2007).
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Сформулюйте та доведіть теорему про добуток суми і різниці одночленів.
2. Запишіть формулу різниці квадратів.
3. Чому дорівнює квадрат різниці одночленів?
4. Чому дорівнює квадрат суми одночленів?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
585. Укажіть правильне твердження:
1) добуток суми і різниці двох одночленів дорівнює сумі їх квадратів;
2) добуток суми і різниці двох одночленів дорівнює різниці їх квадратів;
3) добуток суми і різниці двох одночленів дорівнює добутку їх квадратів.
586. Чи правильно, що:
1) (а + b)(а – b) = а2 + b2; 3) (а + b)(a – b) = а – b;
2) (а + b)(а – b) – а2 – 2b2, 4) (а + b)(а – b) = а2 – b2?
587. Укажіть правильну формулу:
1) а2 – b2 = (а – b)(а – b); 3) а2 – b2 = (а – b)(а + b);
2) а2 – b2 = (а + b)(a + b); 4) а2 – b2 = (2а + 2b)(2а – 2b).
588. Чи є тотожністю рівність:
1) (а – b)(а + b) = а2 – b2; 3) (b + b)(а + а) = b2 + а2;
2) (b – а)(а – b) = b2 – а2; 4) (b – а)(b + а) = b2 – а2?
589. Який із наступних виразів дорівнює добутку (х + у)(х – у):
1) х2 + у2; 3) у2 – x2;
2) х2 – у2; 4 )х2 + у2 + ху?
590. Чи правильно, що (х – 5)(х + 5) дорівнює:
1) х2 + 25; 2) х2 – 25; 3) х2 – 5; 4)х – 25?
591. Чи правильно, що (d – 4)(d + 4) дорівнює:
1) d2 + 16; 2) d – 16; 3)d2 – 16; 4)d -16?
592. Яка із наступних рівностей є тотожністю:
1) (3 – а)(3 + а) = 9 + а2; 3) (3 – а)(3 +а) = 9 – а;
2) (3 – а)(3 + а) = а2 – 9; 4) (3 – а)(3 + а) = 9 – а2?
593. Який із наступних виразів дорівнює виразу (2 + За)(2 – 3а):
1)4 + 9а2; 2)4 – 3 а2; 3)4 – 9а2; 4) 4 – 3 а2?
594. Чи правильно, що 49 ∙ 51 =…
1) (50 – 1)(50 + 1) = 502 + 12 = 2500 + 1 = 2501;
2) (50 – 1 )(50 + 1) = 502 – 12 = 2500 -1 = 2499;
3) (50 – 1)(50 + 1) = 502 + 12 – 2 ∙ 50 ∙ 1 = 2500 + 1 – 100 = 2401?
У неправильних рівностях укажіть, де допущено помилку.
595. Який із наступних виразів дорівнює виразу (2а + 5b)(2а – 5b):
1) 4а2 + 25b2; 3)2а2 – 5b2;
2) 4а2 – 5b2; 4) 4а2 – 25b2?
596. Яка з наступних рівностей є тотожністю:
1) (3 + 4с)(3 – 4с) = 9 – 4с2; 3) (3х + 2у)(3х – 2у) = 9х2 – 4у2;
2) (3 + 4c)(3 – 4с) = 9 – 16с2; 4) (3х + 2у)(3х – 2у) = 9х2 – 4у?
597. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) (2а – 5b)(2а + 5b) = * – 25b2;
2) (9х – 3b)(9х + 3b) = 81х2 – *;
3) ( D + 5c)(5c –
D + 5c)(5c –  D) = 25c2 – *;
D) = 25c2 – *;
4) (2х – 6ху)(2х + 6ху) = * – 36х2у2.
598. Подайте у вигляді многочлена вираз:
1) (х + 3у)(-х + 3у); 3) (с + 5d)(5d – с);
2) (а + 2b)(а – 2b); 4) (-х + 6у)(6у +х).
599. Подайте у вигляді многочлена вираз:
1)(t + 4z)(-t + 4z); 2)(d + 6c)(6c – d).
600. Спростіть вираз:
1) (- X + 2y)(
X + 2y)(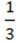 X + 2y);
X + 2y);
2) (2a –  B)(
B)(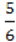 D + 2a);
D + 2a);
3) (0,1с +4d)(4d – 0,1с);
4) (-1,1х + 10y)(10y + 1,1 х).
601. Подайте у вигляді многочлена вираз:
1) (2b + 5d)(2b – 5d);
2) (4ху + 2)(2 – 4ху);
3) (-0,2b +  D)(0,2b +
D)(0,2b +  D);
D);
4) (9xy – 4a)(4a + 9xy).
602. Чи правильно, що а2 – 16 дорівнює:
1) (а – 16)(а + 1); 3) (а – 4)(а + 4);
2) (а – 4)2; 4) (а + 4)(а + 4)?
603. Яка із наступних рівностей є тотожністю:
1) 16 – с2 = (16 – с)(16 + с);
2) 16 – с2 = (4 – с2)(4 + с2);
3) 16 – с2 = (4 – с )(4 + с)?
604. Чи правильно, що 292 – 212 =…
1) (29 – 21 )(29 – 21) = 8 ∙ 8 = 64;
2) (29 + 21 )(29 – 21) = 50 ∙ 8 = 400;
3) (29 + 21 )(29 + 21) = 50 ∙ 50 = 2500;
4)29 – 21 = 8?
У неправильних рівностях укажіть, де допущено помилку.
605. Чи є тотожністю наступна рівність:
1)4х2 – у2 = (2х – у)(2х + у);
2) 25 – 9с2 = (5 – 3с)(5 + 3с);
3) 81 – 25d2 = (9 + 5d)(5d – 9);
4) 36а2 – 4b2 = (4а – 6b)(4a + 6b)?
606. Чи є тотожністю наступна рівність:
1)16а2 – 25с2 = (4а + 5с)(4а – 5с);
2) 64b2 – 9t2 = (3b – 8t)(3t + 8b)?
607. Якому з наступних виразів тотожно дорівнює двочлен 4х4y10 – 36:
1) (2х2у2 – 6)(2х2у2 + 6); 3) (2x2y5 – 6)(2x2y5 + 6);
2) (2х4y5 – 4)(2x4y5 + 4); 4) (4х2y5 – 6)(4х2у5 + 6)?
608. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) 4а2b2 – 25 = (* – 5)(* + 5);
2)9а2 –  С2 = (3а – *)(3а + *);
С2 = (3а – *)(3а + *);
3) 0,16а2b4 –  с4 = (0,4аb2 – *)(0,4аb2 + *).
с4 = (0,4аb2 – *)(0,4аb2 + *).
609. Подайте у вигляді добутку двочлен:
1) 36х2y8 – 16; 3) 49с2 – 9d8;
2) 81а6 – 4b4; 4) 64а2 – 100с12.
610. Подайте у вигляді добутку двочлен:
1) 25 – 16x2y2; 3) 16 – 9c4d8;
2) 49а14 – 9b6; 4) 100а2 – 4с20.
611. Подайте у вигляді добутку двочлен:
1) 0,36х2 – 0,16; 3) 0,49 – 0,01d2;
2)  C2 –
C2 – 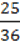 ; 4)
; 4) 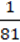 –
– 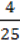 Y2.
Y2.
612. Подайте у вигляді добутку двочлен:
1) -9 + 100t2; 3)-4a2 + 9b2;
2) – х2 + 16y2; 4)-36c2 + 0,25.
613. Подайте у вигляді добутку двочлен:
1) 0,09с2 – 0,04; 3) -25+ 121z2;
2)  B2 –
B2 – 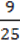 ; 4) -49х2+ 16.
; 4) -49х2+ 16.
614. Використовуючи формулу різниці квадратів, обчисліть:
1) 702 – 682; 3)63 ∙ 57;
2) 1,012 – 0,992; 4)10,5 ∙ 9,5.
615. Використовуючи формулу різниці квадратів, обчисліть:
1) 252 – 242; 3)0,97 – 1,03;
2) 10,22 – 9,82; 4)503 – 497
616.Спростіть вираз:
1) (5 + b)2 – b2; 3) 49у2 – (5 + 7у)2;
2) (4 – 2b)2 – 4b2; 4) 25х2 – (5х + 1 )2
617. Подайте у вигляді добутку вираз:
1) (2х2y2 + ху)2- х2у2;
2) ( A2b2 + 4)2 – 16;
A2b2 + 4)2 – 16;
3) (0,2c2d2 + cd)2 – 0,04c4d4;
4)(5х4 + 6у2)2 – 36у4.
618. Подайте у вигляді добутку вираз:
1) (а2с2 + 3ас)2 – 9а2с2;
2) ( X2y + 5)2 – 25;
X2y + 5)2 – 25;
3) (0,6с6 + d)2 – 0,36с12;
4)(1,1а4 + 4d6)2 – 1,21а6.
619. Спростіть вираз і знайдіть його значення:
1) (1 + 0,1х)(-0,1х + 1) – 1, якщо х= 10;
2) (2х + 6)(2х – 6) + 9 (4 – х), якщо х = 2.
620. Розв’яжіть рівняння:
1) (2х – 1)2 – 4х2 = 0; 3) (5 + х)2 – х2 = 5х;
2) х2 – (6 + х)2 = 9х; 4) 25х2 – (7 – 5х)2 = 14х.
621. Розв’яжіть рівняння:
1)9х2 – (4 – Зх)2 = 0. 2) (7х – 2)2 – 49х2 = 2х.
622. Подайте у вигляді многочлена:
1) (-а – 0,6bс)(а – 0,6bс);
2) (-0,01 ху – 5)(5 – 0,01 ху);
3) (5ax3 –  )(-
)(- – 5ax3);
– 5ax3);
4) (-a3х – ах3)(-а3х + ах3).
623. Доведіть тотожність:
1) (а + b)2 – (-а – b)2 = 0;
2) (а + b)2 – (а – b)2 = 4 аb;
3) (b – 2а)2 – (b – а)2 = 3а2 – 3b2.
624. Подайте у вигляді многочлена:
1) (а +2b)(а – 2b)(а2 + 4b2);
2) (2 + х)(2 – х)(4 + х2);
3) (x – y)(y + х)(у2 + х2).
625. Спростіть вираз:
1) (-0,5xy – 2)(2 – 0,5xy);
2) (5bc4 – 1 )(-1
)(-1 – 5bc4);
– 5bc4);
3) (3 + а)(3 – а)(а2 + 9);
4) (5 + bс)(5 – bс)(25 + b2с2).
626. Спростіть вираз і знайдіть його значення:
1) (1 + х)( 1 – х)( 1 + х2)( 1 + х4), якщо х = 2;
2) (2а + 3b)(-2а + 3b)(4а2 + 9b2), якщо а = 3, b = 2.
627. Доведіть, що:
1) 342 – 1 ділиться на 11;
2) 532 – 4 ділиться на 5;
3) 1112 – 9 ділиться на 12.
628. Виконайте дії:
1) (а + b + с)(а + b – с);
2) (a – b + с)(а + b – с);
3) (а – b + с)(a – b – с).
629. Спростіть вираз:
1) (х + y + 2)(х – y + 2);
2) (ху + х2 + y2)(xy – х2- у2);
3 )(х – у – z)(х + у – z).
630. Сторона одного квадрата на 4 см більша за сторону іншого, а різниця їх площ дорівнює 24 см2. Знайдіть периметри цих квадратів.
631. Периметр одного квадрата на 48 см більший за периметр іншого, а різниця їх площ дорівнює 288 см2. Знайдіть сторони цих квадратів.
632. Сторона одного квадрата на 6 см менша від сторони іншого, а різниця їх площ дорівнює 64 см2. Знайдіть відношення довжин сторін цих квадратів.
633. Доведіть, що:
1) 992 + 202 = 1012;
2) 1122 + 152 = 1132;
3) 102 + 112 + 122 = 132 + 142.
634. Доведіть, що квадрат непарного натурального числа при діленні на 8 дає в остачі 1.
635. Доведіть тотожність: (2n2 + 2n + 1 )2- (2n2 + 2n)2 = (2n + 1)2.
636. Обчисліть: (1 + 2)(1 + 22)(1 + 24)(1 + 28)(1 +216).
637. Різниця квадратів двох двоцифрових натуральних чисел, записаних тими самими цифрами, дорівнює 495. Знайдіть ці числа.
638. Дано три послідовні непарні натуральні числа. Відомо, що різниця квадратів двох більших чисел менша за квадрат найменшого числа на 65. Знайдіть ці числа.
ЗАСТОСУВАННЯ НА ПРАКТИЦІ
639. Тато вирішив переклеїти шпалери в дитячій кімнаті. Стіна з вікном має форму квадрата зі стороною 3,2 м, вікно також має форму квадрата зі стороною 1,3 м. Чи вистачить татові шпалер для поклейки цієї стіни, якщо він купив 2 рулони розміром 10 м х 0,53 м?
640. Чи є рівними площі зафарбованої частини фігур на малюнку 8?
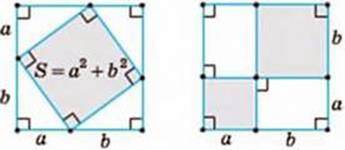
Мал. 8
ЗАДАЧІ НА ПОВТОРЕННЯ
641. Знайдіть значення виразу:
1) 3а + 5b, якщо а =  , b =
, b =  ;
;
2) 0,4с + 0,16с2 + 16, якщо с = -5.
642. Піднесіть одночлен 2а2b3с6 до: 1) квадрата; 2) куба; 3) четвертого степеня.
643. Вкладник вніс до банку 5000 грн, а через рік отримав 5750 грн. Під який відсоток річних були покладені гроші? Скільки грошей отримає вкладник через три роки?
644. Зі слова “математизований” навмання обирають одну літеру. Яка ймовірність того, що виберуть літеру “а”?