Різниця квадратів. (Добуток різниці двох виразів на їх суму)
Урок № 46
Тема. Різниця квадратів (Добуток різниці двох виразів на їх суму)
Мета: відпрацювати навички застосування формули (a – b)(a + b) = a2 – b2 для перетворення цілих виразів у багаточлен стандартного вигляду із застосуванням переставного та сполучного законів множення та залежностей між знаком множників та добутком цих множників; поглибити знання та вміння учні” за рахунок прийому множення та означення ділення даного виразу на один і той самий вираз, то не дорівнює 0.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I.
@ Учитель спонукає учнів до самоперевірки готовності до уроку; записує прізвища відсутніх, розв’язує організаційні питання.
II. Перевірка домашнього завдання
@ № 1 та 2 є вправами на закріплення вироблених на попередньому уроці вмінь, тому перевірку цієї частини домашнього завдання організовуємо так:
Ігровий момент “Знайди помилку”
Учитель пропонує учням розв’язування домашніх вправ (або записані на дошці, або у вигляді роздавального матеріалу) із навмисно “допущеними” типовими помилками і пропонує учням знайти та виправити їх (самостійно). По виконанні
III. Формулювання мети і завдання уроку
@ Учитель говорить про те, що на попередньому уроці учні дізнались про формулу різниці квадратів та її застосування для перетворення найпростіших виразів, а мета цього уроку – навчитися застосувати ці знання і вміння для перетворення більш складних виразів із застосуванням набутих знань та вмінь.
IV. Робота з випереджальним домашнім завданням
Фронтальна бесіда (за питаннями № 3 домашнього завдання)
1. Який закон множення використовується при множенні трьох і більше множників? (Сполучний)
2. Як зміниться добуток двох виразів, якщо змінити: а) знак одного множника; б) знаки обох множників? (а) Добуток тільки змінить знак; б) добуток не зміниться)
3. Яким стане вираз, якщо змінити знак на протилежний: a; (-a + b); (-a – b); (- c – d + а); (-с – d – а)? (-a; a – b; a + b; c + d – a; c – d + a)
@ Після цього учням пропонується за результатами бесіди виконати завдання 1.
Змінивши знак одного або двох багаточленів, виконайте множення за відповідною формулою скороченого множення (якщо це можливо).
1) (-b + c)(-b – с); 2) (-х – у)(х – у); 3) (-а – b)(-b – а); 4) (-b – с)(-с – d).
(Бажано звернути увагу учнів на те, що зміна знака виразу повинна бути обгрунтована, треба, щоб учні розуміли, в яких випадках це перетворення є необхідним, а в яких – без нього можна обійтися.) По виконанні завдання бажано, щоб учні усвідомили, що у випадках, подібних до 1) – 4), перед застосуванням формули слід перетворити вираз, щоб він набув саме того вигляду, що закладений у формулу.
V. Розширення знань
@ На уроці починаємо роботу зі знайомства учнів із нестандартними видами тотожних перетворень, а саме – із перетворенням, що можна записати у вигляді формули:
A • b : b = a. (*) Цю роботу можна провести, запропонувавши учням низку завдань (кожне наступне завдання є логічним продовженням попереднього).
Завдання. Спростіть (найзручнішим способом):
А) (а – 1)(а + 1); (а2 – 1)(а2 + 1); (а4 – 1)(а4 + 1);
Б) (а – 1)(а + 1)(а2 + 1);
В) (а – 1)(а + 1)(а2 + 1)(а4 + 1);
Г) (а + 1)(а2 + 1)(а4 + 1).
Після виконання вправ а) – б) (вони не повинні викликати в учнів труднощів за правильної розстановки акцентів) бажано спочатку сформулювати узагальнення:
(а – b)(а2 + b2)(а4 + b4)(а8 + b8) … (а2n + b2n) = (а2n)2 – (b2n)2 (**)
– і тільки після цього – запропонувати вправу г). Якщо в учнів виникають труднощі з відповіддю, можна запропонувати їм виконати порівняння г) з умовою (**). У будь-якому разі по завершенні цієї роботи учні повинні усвідомити:
1) формулу різниці квадратів можна застосовувати для перетворення виразу кілька разів;
2) наслідком формули різниці квадратів може бути формула (**);
3) якщо даний вираз має вигляд (а + b)(а2 + b2)(а4 + b4)…, то для перетворення його за формулою (*) можна використати прийом, виражений формулою (*).
VI. Засвоєння навичок, вироблення вмінь
Виконання письмових вправ
1. Виконайте множення:
1) (0,4m5 + 0,1n3)(0,1n3 – 0,4m5);
2) (-а8 – b3 )(b3 – а8);
3) 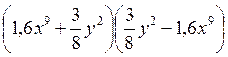 ;
;
4) (а3 – b3)(а3 + b3)(а6 + b6);
5) (b + 1)(b – 1)(b2 + 1);
6) (2х – 1)(2х + 1)(4х2 + 1);
7) (а – 2)(а + 2)(а2 + 4)(а4 + 16);
8) (а – b)(а + b)(а2 + b2)(а4 + b4)(а8 + b8);
9) ((а + b) – с)((а + b) + с).
2. Спростіть вирази:
1) 0,6m(2m – 1)(2m + 1) – 0,8(3 – 5m)2 + 0,4(6 + 7m)(6 – 7т);
2) 4(с – 3)2(с + 3)2 – 3(с + 4)2(4 – с)2.
3. Розв’яжіть рівняння:
1) (6х – 7)2 – 5(2х – 5)(2х + 5) – 2(4х – 15)(2х – 4) = -2;
2) (х – 1)(х + 1)(х2 + 1)(х4 + 1) = х8 + х.
4. Доведіть, що (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1) = 232 – 1.
VII. Підсумки уроку
Тестові завдання
1. Виконайте дії: (5 + 6х)(6х – 5).
1) 25 – 36х2;
2) 36х2 + 25;
3) 36х2 – 60х + 25;
4) 36х2 – 25.
2. Замініть? одночленом так, щоб утворилась тотожність
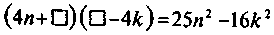
1) 5n; 2) 25n; 3) 5n2; 4) 5n4.
3. Спростіть вираз (b + 4)(b2 – 16)(b – 4).
1) b4 – 32b2 + 256;
2) b4 – 256;
3) 256 – b4;
4) b4 + 32b2 + 256.
VIII. Домашнє завдання
Використовуючи знання формул скороченого множення, виконайте вправи.
№ 1. Знайдіть значення виразу, спростивши попередньо вираз:
1) (m + 5)2 + (-m – 4)(m – 4), якщо m = -3,5;
2) (аb – 1)(аb + 1)(а2b2 + 1)(а4b4 + 1), якщо а = 5, b = -0,2;
3) (а3 – 2)(а3 + 2) – (а3 + 3)2, якщо а = -2.
№ 2. Доведіть тотожність (а + b)(а2 + b2)(а4 + b4)(а8 + b8) = а16 – b16, якщо а – b = 1.
№ 3. Випереджальне домашнє завдання. Використовуючи правило множення багаточлена на багаточлен, виконайте множення. Спростіть, порівняйте, зробіть висновки:
1) (a – b)(a2 + ab + b2);
2) (a + b)(a2 – ab + b2);
3)(c – d)(c2 + cd + d2);
4) (c + d)(c2 – cd + d2);
5) (m – 1)(m2 + m + 1);
6) (m + 1)(m2 – m + 1).