Головна ⇒ 📌Довідник з математики ⇒ Розкриття дужок
Розкриття дужок
Математика – Алгебра
Раціональні числа
Розкриття дужок
Щоб розкрити дужки, перед якими стоїть знак “+”, треба опустити дужки і знак “+”, що стоїть перед ними, і записати всі доданки зі своїми знаками.
Щоб розкрити дужки, перед якими стоїть знак “–”, треба опустити дужки і знак “–”, що стоїть перед ними, і записати всі доданки з протилежними знаками.
Приклади
1) 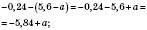
2) 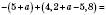
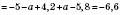 .
.
Related posts:
- Розкриття дужок Розділ 4 Раціональні числа і дії мідними §42. Розкриття дужок Згадаємо, як до числа а додати суму чисел b і c. Можна спочатку до а додати b, а потім до отриманого результату додати c: А + (b + c) = а + b + c. Ми записали вираз а + (b + c) без дужок. […]...
- Розкриття дужок Урок № 77 Тема. Розкриття дужок Мета: відпрацювати навички застосування вивчених правил для розв’язування завдань, що передбачають як розкриття дужок, так і заключення кількох доданків у дужки; вдосконалювати вміння обчислювати значення та спрощувати алгебраїчні суми. Тип уроку: застосування знань, умінь і навичок. Хід уроку І. Перевірка домашнього завдання @ Ретельно перевіряємо вправи на використання правил […]...
- Перетворення виразів (повторення та систематизація матеріалу, вивченого в 5 та 6 класах) Урок № 2 Тема. Перетворення виразів (повторення та систематизація матеріалу, вивченого в 5 та 6 класах) Мета: повторити та систематизувати відомості про види перетворень виразів та способи дій, передбачених ними, що були отримані учнями в 5-6 класах в обсязі, необхідному для сприйняття теми “Рівняння”. Тип уроку: повторення, систематизація знань, умінь, навичок. Хід уроку I. Організаційний […]...
- Множення Математика – Алгебра Раціональні числа Множення Щоб знайти добуток двох чисел із різними знаками, треба перемножити їхні модулі й поставити перед одержаним числом знак “–”. Щоб перемножити два від’ємних числа, треба перемножити їхні модулі (тобто добуток двох від’ємних чисел є додатне число). При зміні знака одного з множників змінюється знак усього добутку. Якщо добуток містить […]...
- Додавання раціональних чисел Математика – Алгебра Раціональні числа Додавання раціональних чисел Щоб додати два від’ємних числа, треба додати їхні модулі й поставити перед одержаним числом знак “–”: . Щоб додати два числа з різними знаками, треба від більшого модуля відняти менший і поставити перед одержаним числом знак того доданка, модуль якого більший: ; . Сума двох протилежних чисел […]...
- ВІДОМОСТІ З КУРСУ МАТЕМАТИКИ 5-6 КЛАСІВ ВІДОМОСТІ З КУРСУ МАТЕМАТИКИ 5-6 КЛАСІВ Натуральні числа Числа 1, 2, 3, 4, 5, … , які використовують для лічби предметів, називають натуральними числами. Найменше натуральне число дорівнює 1, найбільше не існує. При округленні натурального числа до повного розряду всі наступні за цим розрядом цифри замінюють нулями. Якщо перша наступна за цим розрядом цифра 5, […]...
- ВИРАЗИ ТА ЇХ СПРОЩЕННЯ Розділ 5 ВИРАЗИ І РІВНЯННЯ У розділі дізнаєтесь: Ü про вирази та їх спрощення; Ü які є властивості рівностей; Ü як розв’язувати рівняння на основі властивостей рівностей; Ü які види задач розв’язують за допомогою рівнянь; що таке перпендикулярні прямі та як їх будувати; Ü які прямі називаються паралельними та як їх будувати; Ü що таке […]...
- Додавання і віднімання дробів з однаковими знаменниками Математика – Алгебра Звичайні дроби Додавання і віднімання дробів з однаковими знаменниками Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і суму записати в чисельнику, а знаменник залишити той самий: . Щоб відняти дроби з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від’ємника й різницю записати в чисельнику, а знаменник залишити той […]...
- Додавання і віднімання багаточленів Урок № 33 Тема. Додавання та віднімання багаточленів Мета: вдосконалити вміння учнів перетворювати суму та різницю багаточленів у багаточлен стандартного вигляду; виробити вміння виконувати обернені перетворення (заключати кілька членів багаточлена в дужки, перед якими стоїть певний знак); здійснити проміжну діагностику рівня засвоєння знань та вмінь. Тип уроку: застосування знань, умінь та навичок. Хід уроку І. […]...
- Метод інтервалів Математика – Алгебра Границя Метод інтервалів Отже, нехай функція неперервна на інтервалі І й перетворюється на 0 у скінченній кількості точок цього інтервалу. Тоді інтервал І розбивається цими точками на інтервали, в кожному з яких зберігає незмінний знак. Щоб визначити цей знак, достатньо обчислити значення у будь-якій точці кожного такого інтервалу. Приклад Розв’язати нерівність Розглянемо […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- Розв’язування рівнянь Математика – Алгебра Раціональні числа Розв’язування рівнянь Властивості рівнянь Корені рівнянь не змінюються, якщо до обох частин додати будь-який доданок. Отже, при розв’язуванні рівнянь доданки можна переносити з однієї частини в другу, змінюючи при цьому їхні знаки на протилежні. Корені рівнянь не змінюються, якщо обидві його частини помножити або поділити на одне й те ж […]...
- ПЕРЕТВОРЕННЯ ВИРАЗІВ РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ &3. ПЕРЕТВОРЕННЯ ВИРАЗІВ Ви вже знаєте, що два числові вирази МОЖУТЬ мати рівні значення, і тоді ці вирази можна прирівняти. Наприклад, 10 ∙ 2 + 5 = 31 – 2 ∙ 3. Про вирази зі змінними такого однозначно сказати не можна. Розглянемо приклади. Задача 1. Чи можна прирівняти вирази: 1) […]...
- Ділення раціональних чисел Математика – Алгебра Раціональні числа Ділення раціональних чисел Часткою двох від’ємних чисел є число додатне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Часткою двох чисел із різними знаками є число від’ємне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Для будь-якого числа а: ; ; Для : ; […]...
- Множення, ділення й піднесення до степеня дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Множення, ділення й піднесення до степеня дробів Щоб помножити дріб на дріб, треба перемножити окремо їхні чисельники й окремо знаменники і перший добуток записати чисельником, а другий – знаменником дробу. Щоб піднести дріб до степеня, треба піднести до цього степеня чисельник та знаменник і перший результат записати чисельником, а другий […]...
- Множення звичайних дробів Математика – Алгебра Множення і ділення звичайних дробів Множення звичайних дробів Добутком звичайних дробів є дріб, чисельник якого дорівнює добутку чисельників цих дробів, а знаменник дорівнює добутку їхніх знаменників. (Отриманий дріб, як правило, скорочують.) Наприклад: . Щоб помножити дріб на натуральне число, його чисельник помножують на це число, а знаменник залишають без зміни. Наприклад: ; […]...
- ПОРЯДОК ДІЙ У ВИРАЗАХ НА ДІЇ РІЗНИХ СТУПЕНІВ БЕЗ ДУЖОК І З ДУЖКАМИ. ВПРАВИ НА ЗАПАМ’ЯТОВУВАННЯ ТАБЛИЦІ МНОЖЕННЯ ЧИСЛА 3 Мета: ознайомити учнів з порядком дій у виразах на дії різних ступенів без дужок і з дужками; формувати навички табличного множення числа 3; розвивати логічне мислення, пам’ять, увагу; виховувати акуратність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 108, завдання 634; 635) Завдання 634 – Прочитайте вирази, у яких […]...
- Многочлен Математика – Алгебра Многочлен Многочленом Називається сума кількох одночленів. Одночлени, які складають многочлен, називаються його членами. Подібні доданки многочлена називають Подібними членами многочлена. Многочлен, що є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називається Многочленом стандартного вигляду. Степенем многочлена Стандартного вигляду називається степінь одночлена, який є найбільшим серед степенів одночленів, що утворюють даний […]...
- Перетворення звичайного дробу в десятковий і навпаки Математика – Алгебра Порівняння та округлення натуральних чисел і десяткових дробів Перетворення звичайного дробу в десятковий і навпаки Будь-який десятковий дріб можна записати як звичайний із знаменником виду 10, 100, 1000 і так далі: ; ; . Щоб перетворити звичайний дріб на десятковий, треба чисельник поділити на знаменник за правилом ділення десяткових дробів. Інколи таке […]...
- Відсотки Математика – Алгебра Відсотки Відсотком називають (0,01) і позначають 1%. Один відсоток від якої-небудь величини означає 0,01 цієї величини. Наприклад, 1% від 500 м дорівнює 5 м; 4% від 320 т дорівнюють (т). 100% деякої величини – це сама величина. Будь-який десятковий дріб можна записати у відсотках. Для цього його треба помножити на 100: ; […]...
- Множення одночлена на многочлен Математика – Алгебра Многочлен Множення одночлена на многочлен Щоб помножити одночлен на многочлен, треба одночлен помножити на кожний член многочлена й одержані добутки додати. Тобто множення одночлена на многочлен здійснюється на основі розподільної властивості множення....
- Застосування кількох способів для розкладання многочленів на множники Математика – Алгебра Многочлен Застосування кількох способів для розкладання многочленів на множники Щоб розкласти многочлен на множники, бажано діяти в такій послідовності. 1. З’ясувати, чи можна винести за дужки спільний множник. Зробити це, якщо можна. 2. Розглянути, чи можна вираз, який залишився в дужках (або даний), розкласти на множники за формулами скороченого множення. 3. Спробувати […]...
- Розкладання многочленів на множники Математика – Алгебра Многочлен Розкладання многочленів на множники Розкласти многочлен на множники означає подати його як добуток кількох многочленів. Винесення спільного множника за дужки Спосіб розкладання многочлена на множники на основі розподільної властивості множення називається винесенням спільного множника за дужки. Приклад . НСД . Це означає, що за дужки можна винести числовий множник 2. В […]...
- Звичайні дроби Математика – Алгебра Звичайні дроби Записи виду називаються звичайними дробами, або дробами. Звичайні дроби записують за допомогою двох натуральних чисел та горизонтальної риски, яка називається дробовою рискою. Число, записане під рискою, називається знаменником дробу, а число, записане над рискою, – чисельником. Знаменник показує, на скільки рівних частин поділено одиницю (ціле), а чисельник – скільки таких […]...
- ДОДАВАННЯ І ВІДНІМАННЯ. ПОРІВНЯННЯ КІЛЬКОСТІ ПРЕДМЕТІВ. ЗНАКИ “+” І “-“. НАПИСАННЯ ЗНАКІВ “+” І “-“ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 15. ДОДАВАННЯ І ВІДНІМАННЯ. ПОРІВНЯННЯ КІЛЬКОСТІ ПРЕДМЕТІВ. ЗНАКИ “+” І “-“. НАПИСАННЯ ЗНАКІВ “+” І “-“ Мета: ознайомити учнів зі знаками дій додавання і віднімання, вчити їх писати, порівнювати кількість предметів; розвивати мовлення; виховувати інтерес до предмета. Хід уроку I. ОРГАНІЗАЦІЙНИЙ […]...
- Натуральні числа і дії над ними Математика – Алгебра Натуральні числа і дії над ними Числа, які використовуються при лічбі предметів, називаються Натуральними числами. Натуральний ряд чисел є нескінченним. Він записується так: 1, 2, 3, … 0 не є натуральним числом. Зазвичай прийнято користуватись Позиційною десятковою системою числення. Тобто кожне число може бути записане за допомогою десяти цифр (0, 1, 2, […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Додавання двох чисел з різними знаками Розділ 4 Раціональні числа і дії мідними §39. Додавання двох чисел з різними знаками Припустимо, що в понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув борг, тобто віддав Сергію 3 грн. Оскільки борг можна тлумачити як від’ємні числа, а майно – як додатні, то розрахунок між хлопцями можна подати так: -3 + 3 […]...