Розкриття дужок
Розділ 4 Раціональні числа і дії мідними
§42. Розкриття дужок
Згадаємо, як до числа а додати суму чисел b і c. Можна спочатку до а додати b, а потім до отриманого результату додати c:
А + (b + c) = а + b + c.
Ми записали вираз а + (b + c) без дужок. Таке перетворення виразу називають розкриттям дужок.
Приклад 1. Розкрити дужки у виразі а + (b – c).
Розв’язання. а + (b – c) = а + (b + (-c)) = а + b + (-c) = а + b – c.
Приклад 2. Розкрити дужки у виразі а + (-b – c).
Розв’язання. а + (-b – c) = а + ((-b) + (-c)) = а + (-b) + (-c) = а – b – c.
Вираз а + b – c можна отримати
– щоб розкрити дужки, перед якими стоїть знак “+”, треба не писати дужки і знак “+”, що стоїть перед ними, та записати всі доданки зі своїми знаками.
Приклад 3. Розкрити дужки і знайти значення виразу 5,2 + (-7,2 + 3).
Розв’язання. 5,2 + (-7,2 + 3) = 5,2 – 7,2 + 3 = 1.
Згадаємо і запишемо правило віднімання від числа а суми чисел b і с: а – (b + с) = а – b – с.
Ми записали вираз а
Приклад 4. Розкрити дужки у виразі а – (b – с).
Розв’язання. а – (b – с) = а – (b + (-с)) = а – b – (-с) = а – b + с.
Вираз а – b – с можна отримати з виразу а – (b + с), а вираз а – b + с – з виразу а – (b – с), якщо не писати дужки і знак “-” та записати всі доданки, які були в дужках, з протилежними знаками. Маємо правило розкриття дужок, перед якими стоїть знак “-“:
– щоб розкрити дужки, перед якими стоїть знак “-“, треба не писати дужки і знак “-“, що стоїть перед ними, та записати всі доданки з протилежними знаками.
Приклад 5. Розкрити дужки і знайти значення виразу -4,9 – (5,2 – 8,1).
Розв’язання. -4,9 – (5,2 – 8,1) = -4,9 – 5,2 + 8,1 = -10,1 + 8,1 = -2.
Приклад 6. Спростити вираз:
1) 7 – (а – 8); 2) (x – 5) – (x + 8).
Розв’язання. 1) 7 – (а – 8) = 7 – а + 8 = (7 + 8) – а = 15 – а.
2) Як відомо, при запису додатних чисел знак “+”, як правило, не пишуть. Так само знак “+” не пишуть на початку прикладу перед дужками. Отже, замість + (x – 5) пишуть (x – 5). Маємо:
(x – 5) – (x + 8) = x – 5 – x – 8 = х + (-х) + (-5 – 8) = = 0 + (-13) = -13.
Сформулюй правило розкриття дужок, перед якими стоїть знак “+”. Сформулюй правило розкриття дужок, перед якими стоїть знак “-“.
1130. (Усно) Який знак стоїть перед дужками у виразі:
1) (42 + x) – 5; 2) 37 – (x – 2);
3) – (x + 7) – 8; 4) 13 + (x – 8)?
1131. (Усно) Чи правильно розкрито дужки:
1) (а – 5) + 2 = а – 5 + 2;
2) (m + 3) – (k – 5) = m + 3 – k – 5;
3) 4 + (b – 7) = 4 – b – 7;
4) – (а + b – c) = – а – b + c?
1132. Розкрий дужки:
1) а + (b – 5); 2) (c + 1) + d;
3) – (m – 5); 4) 4 – (m – p).
1133. Розкрий дужки:
1) m + (4 – c); 2) (а – 5) + b;
3) – (9 – n); 4) 5 – (-t + p).
1134. Розкрий дужки і обчисли:
1) 7,3 + (3,5 – 6,3); 2) 3,1 – (5,6 – 6,9);
3) 1,2 – (-1,3 + 1,5); 4) – (7,4 – 10,8) + 1,3;

1135. Розкрий дужки і обчисли:
1) -0,5 + (-4,2 + 3,9); 2) 1,8 – (2,9 – 4,8);
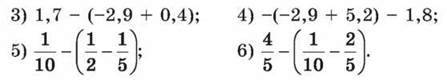
1136. Розкрий дужки і спрости вираз:
1) 0,2 + (a + 2,8); 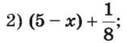
3) – (у – 0,8) + 2; 4) 1,2 – (х + 1,6);
5) (a – 7) – (b + 8); 6) – (a – 5) + (х + 8).
1137. Розкрий дужки і спрости вираз:
1) 1,9 + (3,7 – a); 2) (4 + b) – 3,2;
3) – (p – 4,9) + 0,1; 4) 4 – (m – 3);
5) (m + 1,2) – (n – 1,8); 6) – (х – 2,9) + (y + 5).
1138. Розкрий дужки і спрости вираз:
1) c – (c + m); 2) – (a – b) – b;
3) a + (-a + 5); 4) (m + 9) – (m + 5);
5) – (4 – p) + (-p + 7); 6) – (d – 1,2 + k) – (1,8 – d).
1139. Розкрий дужки і спрости вираз:
1) p – (p – a); 2) – t – (-t + m);
3) c + (d – c); 4) (х – 2) – (х + 3);
5) – (a – 4) + (4 – a); 6) – (m – 1,8 – p) + (1,9 – p).
1140. Запиши суму двох виразів і спрости її:
1) -5 – х і х + 5; 2) 1,9 + p і -3,8 – p;
3) a – b + c і – a + b + 5;
4) -4,2 + 9,8 – х і х – 5,4 + 19,2.
1141. Запиши суму двох виразів і спрости її:
1) 2 + a і -2,8 – a; 2) m – n + 6 і – m – 7 + n.
1142. Запиши різницю двох виразів і спрости її:
1) -4,8 + х і х + 3,2; 2) 4,7 – х і – у + 2,9;
3) a – b і – b + p + a; 4) 5 – 9,2 + m і 4,7 + m – 5,9.
1143. Запиши різницю двох виразів і спрости її:
1) 5 – a і 4,8 – a + b; 2) 4,5 + m – 9,2 і 7,19 + m.
1144. Розкрий дужки і знайди значення виразу:

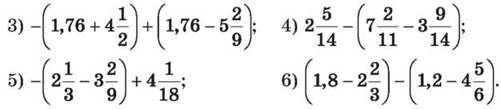
1145. Розкрий дужки і обчисли:
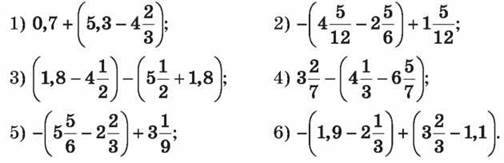
1146. Спрости вираз (x + у) – (x – z) + (p – у) і знайди його значення, якщо 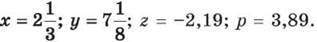
1147. Спрости вираз (а – b) – (а – c) + (b – d) і знайди його значення, якщо 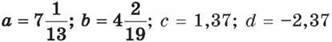
1148. Розв’яжи рівняння, спростивши спочатку вираз у його лівій частині:
1) 7,4 – (x – 2,6) = 19; 2) 4,3 + (3,1 – x) = 12,7;
3) 7,2 – (2,9 + x) = -1,9; 4) -5,2 + (у – 4,2) = -9,4;

1149. Розв’яжи рівняння, спочатку спростивши вираз у його лівій частині:
1) 4,9 – (5,2 – х) = -1,8; 2) 1,93 + (х – 3,93) = -4,01;
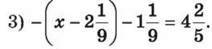
1150. Візьми в дужки три останніх доданки, записавши перед дужками знак “+”:
1) -2 + 3 – 7 + 9; 2) а – b + c – d,
3) – p – 2,5 – c + d; 4) 7,2 – а – b – c.
1151. Візьми в дужки три останніх доданки, записавши перед дужками знак “-“:
1) 5 – 7 + 8 – 18; 2) p – t – а + 9;
3) – а – b – c + d; 4) t – p + 2,9 – а.
Розв’язання. 4) t – p + 2,9 – а = t – (p – 2,9 + а).
1152. Візьми в дужки два останніх доданки, один раз записавши перед дужками знак “+”, а другий – знак “-“:
1) -4 + 5 – 9; 2) p – а + 7; 3) 9 – а – b; 4) а + t + m.
1153. У сумі а + b доданок а зменшили на m, а доданок b збільшили на m. Доведи, що сума залишилася незмінною.
1154. ф Чи є взаємно простими числа 3927 і 2210?
1155. У магазині за три дні продали 1200 зошитів. За перший день продали 28 % усіх зошитів, а за другий – удвічі більше, ніж за третій. По скільки зошитів продавали кожного дня?
1156. Записано чотири числа 2014, 2015, 2017, 2019. За один хід дозволяється додати одиницю до будь-яких двох з них. Чи можна через кілька ходів отримати чотири однакових числа?
Завдання для перевірки знань № 7 (§ 38 – § 42)
1. Виконай додавання:
1) -2 + (-7); 2) -3,1 + (-4,5).
2. Знайди значення суми:
1) -5 + 3; 2) 7,1 + (-3,2).
3. Виконай віднімання:
1) 4 – 7; 2) 5,2 – (-4,7).
4. Виконай дії:
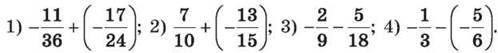
5. Виконай додавання зручним способом: -2,1 + 4,7 + (-3,8) + 2,1 + (-7,3) + 4,9 + (-2,8).
6. Розкрий дужки і знайди значення виразу:
1) 4,1 – (5,9 – 0,8); 2) -4,7 + (-5,7 + 1,9).
7. Спрости вираз – (а + 9) + (m – 7) – (n – а) і знайди його значення, якщо 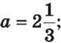 m = 38; n = 22.
m = 38; n = 22.
8. Розв’яжи рівняння, спростивши спочатку вираз у його лівій частині: 4,9 – (x – 5,1) = -13,2.
9. Знайди суму, доданками якої є числа: обернене і протилежне до числа 6,5.
Додаткові вправи
10. Запиши число 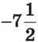 у вигляді суми трьох рівних доданків.
у вигляді суми трьох рівних доданків.
11. Постав замість * знаки “+” або “-“, щоб виконувалася рівність *15 + (*25) * (-30) * (-45) = -55.
12. Візьми в дужки три останніх доданки, один раз постав перед дужками знак “+”, а другий – знак “-“:
1) 4 – 5 + 9 – 11; 2) – m + а – 14 – p.