Розподільна властивість множення
Урок № 86
Тема. Розподільна властивість множення
Мета: повторити розглянуті в 5 класі способи запису та застосування розподільної властивості множення та поширити її на множення раціональних чисел.
Тип уроку: систематизація та узагальнення знань.
Хід уроку
I. Перевірка домашнього завдання
Вибірково перевіряємо зошити.
Усні вправи (фронтально)
1. Обчисліть:
А) 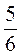 +
+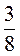 ; б)
; б) 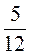 –
– 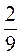 ; в) 2
; в) 2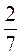 – 1
– 1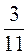
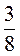 + 1
+ 1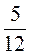 ; д)
; д) 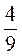 –
– 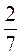 ; є)
; є) 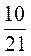 –
– 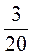 ; ж) 4
; ж) 4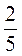 – 5; з) 4
– 5; з) 4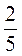 – 10; к)
– 10; к) 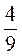 :
: 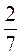 ; л)
; л) 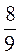 :
: 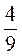 ; м) 0 : 4
; м) 0 : 4 ; н) 1 : 1
; н) 1 : 1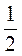 .
.2. Назвіть коефіцієнт виразів: 3ху; – у; -1,2а; – B – 3c; m; -2abc –
B – 3c; m; -2abc – 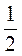 B.
B.
3. Чому дорівнює добуток усіх цілих чисел від -299 до 300 включно?
4. Не обчислюючи, порівняйте
II. Актуалізація опорних знань
1. Як обчислити найзручнішим способом значення виразу: а) 39 – 10 + 10 – 21; б) 45 : 13,5 – 45 – 12,5; в) 4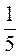 – 5?
– 5?
2. Серед поданих виразів знайдіть пари рівних: а) 5а + 3а; б) 5 – (а + b); в) 3а – а; г) 8а; д) 2а; є) 5а + 5b; ж) 15а2; з) 5а – 3а.
3. Назвіть доданки в сумі -3 + a – 5m – 12 – (-3).
III. Систематизація та узагальнення знань
@ Після виконання завдання 1 та завдання 2 учні “здогадуються”, що мова на уроці піде про використання розподільної властивості множення (учні повинні мати уявлення про цю властивість і способи її використання з 5 класу) для множення раціональних чисел. Тому завданням учителя є не стільки пояснення нового матеріалу, скільки узагальнення та систематизація знань учнів з цього питання. Аналогічно до розглянутого питання “Сполучна і переставна властивості множення” ми працюємо над тим, щоб учні усвідомили, що:
1) розподільна властивість використовується для будь-яких раціональних чисел;
2) розподільна властивість використовується в прямому (розкриття дужок) і зворотному (винесення спільного множника за дужки) порядку;
3) розподільна властивість множення використовується як для спрощення обчислень, так і для спрощення виразів (зведення подібних доданків). Щоб учні мали такі систематизовані уявлення про розподільну властивість множення та її застосування, можна супроводити пояснення записами у вигляді конспекту 34, які учні дублюють у робочих зошитах:
Конспект 34 | |
Розподільна властивість множення | |
1. Розкриття дужок: A(b + c) = ab + ас. 2. Винесення спільного множника за дужки: Ab + ас = а(b + с) | Приклад 1. а) -5(а + 0,3) = (-5) – а + (-5) – 0,3 = -5а + (-1,5) = -5a – 1,5; Б) – 4 2. а) 4 – (-3) + 4 – 7 = 4 – (-3 + 7) = 4 – 4 = 16; Б) 5х – 4х = х(5 – 4) = х – 1 = х. |
IV. Вдосконалення вмінь, відпрацювання навичок
@ Оскільки на вивчення теми програмою відводиться 3 години, автор вважає доцільним розділити навчальний матеріал на дві частини: на цьому уроці займаємося обчисленнями (робота із числовими виразами), на наступному – робота з буквеними виразами; на третьому – узагальнюємо матеріал, пишемо самостійну роботу.
Усні вправи
1. Обчисліть: а) 21 – 3 – 31 – 3; б) 27 – 25 – 17 – 2,5; в) 25 – (-9) + 5 – (-9); г) 54 – (-8) + 54 – 9; д) 25 – 90 +25 – (-86); е) +3 – 3; ж) -3
– 3; ж) -3 – (-9).
– (-9).
2. Прочитайте вираз, використовуючи слова “сума”, “добуток”: -3 – 2 + 3 – 7; -0,3 – 0,2 + 0,1 – (-0,7); -3,4 – 5,4.
Письмові вправи
Обчисліть:
1. а) 54 – 4 – 14 – 54;
Б) -17 – 25 – 5 – (- 17);
В) 2,7 – 19 – 3,7 – 19;
Г) 91 – 31 – 32 – 91 + 91;
Д) 1,4 – 1,9 – 3,2 – 1,4 – 1,4 – 8,7;
Є) -5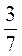 –
– 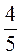 –
– 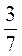 –
– 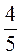 ;
;
Ж) 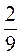 –
– 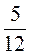 –
– 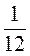 –
– 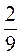 –
–  –
– 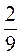 .
.
2. а) 6 – 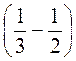 ; б)
; б) 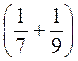 – (-63); в) 12 –
– (-63); в) 12 – 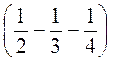 .
.
3. Винесіть за дужки спільний множник і виконайте дії: а) 15 – 19 + 30 – 3; б) 90 – 7 – 60 – 8; в) 50 – 17 + 25 – 3.
4. Обчисліть, використовуючи розподільну властивість множення: а) -23 – (- 99); б) 98 – (-11); в) 999 – (- 17).
5. Обчисліть раціонально:
А) 78 – 62 + 13 – 78 – 75 – 68;
Б) 54 – 36 – 42 – 54 + 6 – 74;
В) 478 – 27 + 28 – 478 – 678 – 55;
Г) 4,8 – 6,5 – 8,5 – 6,8 + 2 – 4,8.
@ Завдання 1. Особливу увагу звертаємо на те, що, перш ніж виносити спільний множник за дужки, треба зрозуміти, які доданки записані (тобто відпрацьовуємо поняття “алгебраїчна сума”).
@ Завдання 2. Знову в дужках маємо алгебраїчну суму, а тому враховуємо це під час множення.
Наприклад
А) 6 – 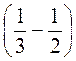 = 6 –
= 6 – 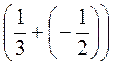 = 6 –
= 6 –  + 6 –
+ 6 – 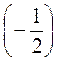 = 2 + (-3) = -1 і т. д.
= 2 + (-3) = -1 і т. д.
Завдання 3. Вправа є підготовчою для вироблення уявлення про спільний множник як найбільший спільний дільник доданків.
Завдання 4. Вчимося використовувати прийоми швидкої лічби – подаємо один з доданків як алгебраїчну суму розрядної одиниці та числа ±1.
Завдання 5. Послідовне кількаразове використання розподільної властивості.
V. Підсумок уроку
Ще раз нагадуємо учням (після розв’язування № 4 та № 5 це дуже наочно), що використання розподільної властивості множення дозволяє в багатьох випадках досить складні дії робити усно.
VI. Домашнє завдання
1. Поставте замість зірочки знак “<” або “>”так, щоб утворилась правильна нерівність: а) -7,2 – (-15) * 100; б) 100 – (- 3) * 300; в) 0,2 – (-14) * -2,5.
2. Обчисліть раціонально: а) 36 – 28 + 36 – 39 – 67 – 46; б) 3,4 – 4,5 – 3,4 – 10,6 + 6,1 – 4,4.
3. Виконайте дії: а) 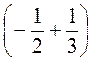 – (-6); б)
– (-6); б) 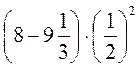 .
.
Додаткова вправа
Як обчислити усно: 11 – 99; (-11) – (-273); 99 – (-273)?
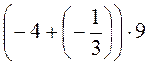 = (-4) – 9 +
= (-4) – 9 + 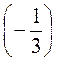 – 9 = -36 + (-3) = -39.
– 9 = -36 + (-3) = -39.