Розв’язання систем лінійних рівнянь способом підстановки
Рівень А
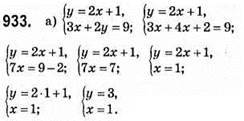
Відповідь: (1; 3).
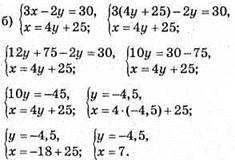
Відповідь: (7; -4,5).
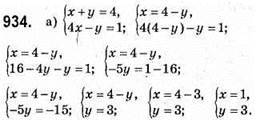
Відповідь: (1; 3).
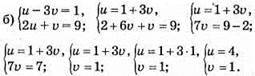
Відповідь: (4; 1).
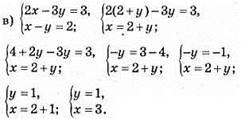
Відповідь: (3; 1).
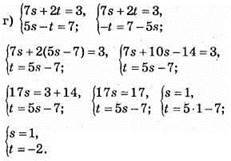
Відповідь: (1;-2).
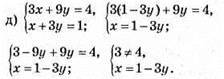
Відповідь: розв’язків немає.
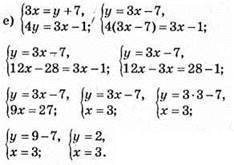
Відповідь: (3; 2).
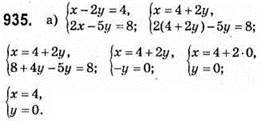
Відповідь: (4; 0).
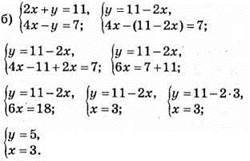
Відповідь: (3; 5).
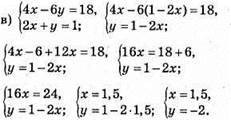
Відповідь:
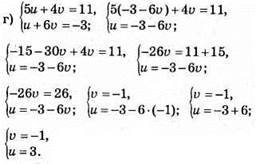
Відповідь: (3; -1).
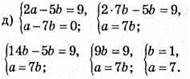
Відповідь: (7; 1).
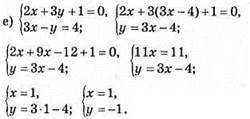
Відповідь: (1; -1).
Рівень Б
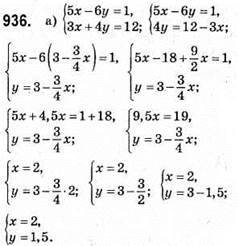
Відповідь: (2; 1,5).
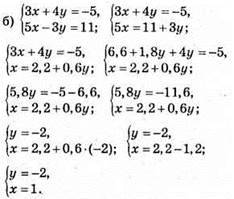
Відповідь: (1; -2).
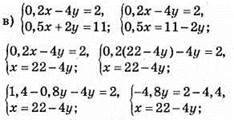
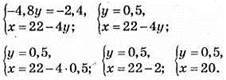
Відповідь: (20; 0,5).
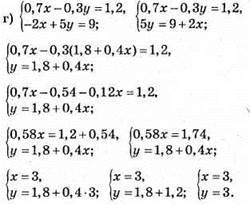
Відповідь: (3; 3).
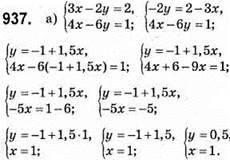
Відповідь: (1; 0,5).
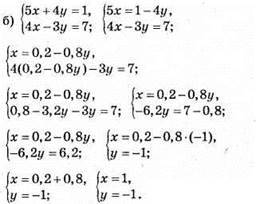
Відповідь: (1; -1).
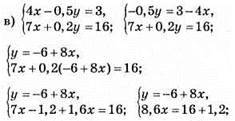
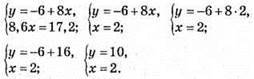
Відповідь: (2; 10).
938. а) х – у = 4 і х + 2у = -2. Для того, щоб знайти координати
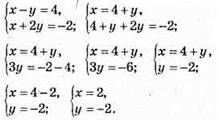
(2; -2) – точка перетину графіків.
Відповідь: (2; -2).
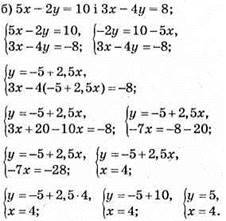
Відповідь: (4; 5).
939. 7х + 4у = 9 i 2х + 5у = -9. Розв’яжемо систему:
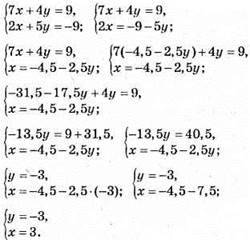
Відповідь: (3; -3).
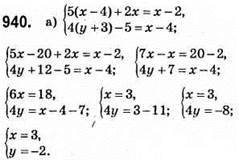
Відповідь: (3; -2).
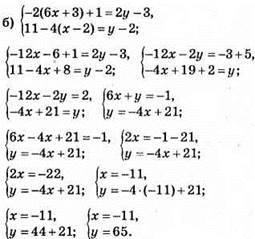
Відповідь: (-11; 65).
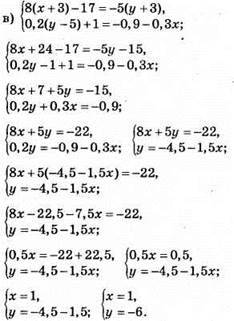
Відповідь: (1; -6).
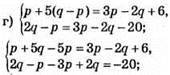
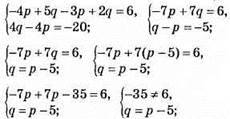
Розв’язків нема.
Відповідь: розв’язків немає.
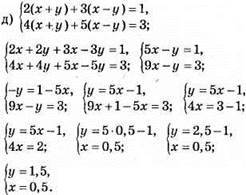
Відповідь: (0,5; 1,5).
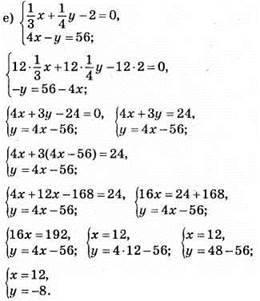
Відповідь: (12; -8).
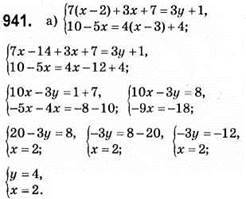
Відповідь: (2; 4).
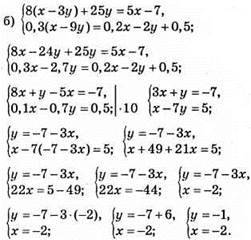
Відповідь: (-2; -1).
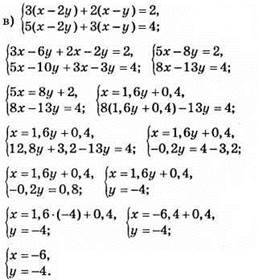
Відповідь: (-6; -4).
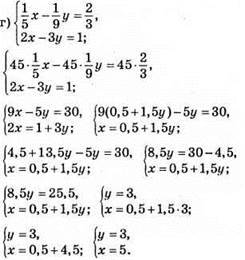
Відповідь: (5; 3).
942. Розв’яжемо систему рівнянь:
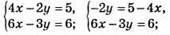
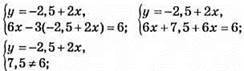
Розв’язків немає, оскільки графіком кожного рівняння системи являється пряма і вони не мають точки перетину, то вони паралельні.
943. A(-2; 6); В(3; 1). у = kх + b – рівняння прямої, координати точок А і В задовольняють рівняння.
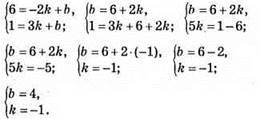
Y = – x + 4 – рівняння прямої, що проходить через точки А(-2; 6) і В(3; 1).
Відповідь: у = – х + 4.
944. А(-3; 2) і В(3; -1). у = kх + b – рівняння прямої. Координати точок А і В задовольняють його.
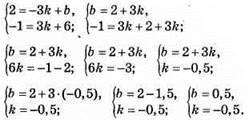
У = -0,5х + 0,5 – рівняння прямої, що проходить через точки А(-3; 2) і В(3; -1).
Рівень В
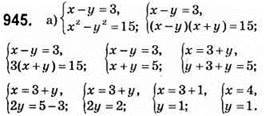
Відповідь: (4; 1).
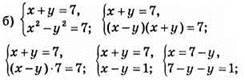
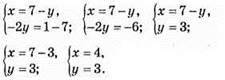
Відповідь: (4; 3).
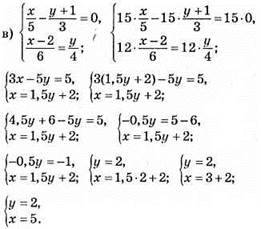
Відповідь: (5; 2).
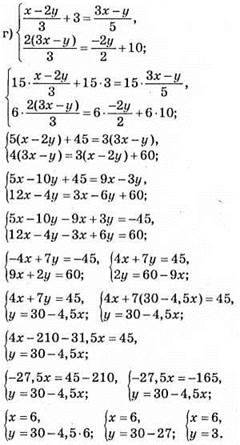
Відповідь: (6; 3).
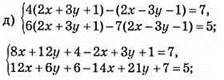

Відповідь: (3/4; -1/6).
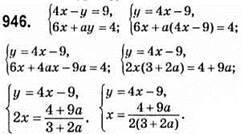
Система не має розв’язку, коли 3 + 2а = 0, оскільки ділити на нуль неможна. Тому 2а = -3; а = -1,5.
Відповідь: а = -1,5.
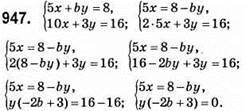
Якщо -2b + 3 = 0, то у – будь-яке число. Тому -2b = -3; b = 1,5.
Відповідь: b = 1,5.
Вправи для повторення
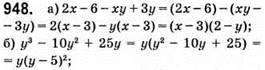
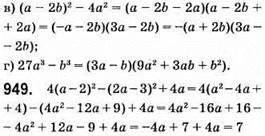
Не залежить від значень а.
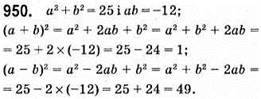
Відповідь: 1; 49.
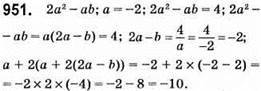
Відповідь: -10.
Related posts:
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...
- Розв’язання систем лінійних рівнянь способом додавання Рівень А Відповідь: (4; 3). Відповідь: (-2; -3). Відповідь: (0,5; 1). Відповідь: (-1;2). Відповідь: (-2; 4). Відповідь: (5; 1). Відповідь: (3; -1). Відповідь: (0; -2). Відповідь: (-1; 3). Відповідь: (-1; -1). Відповідь: (2; -2). Відповідь: (4; -3). Відповідь: (-0,5; 0,5). Відповідь: (1; -1). Відповідь: (1; -2). Відповідь: (1; -2). Відповідь: (5; 6). Відповідь: (5; 0,5). […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...
- Розв’язування систем лінійних рівнянь методом підстановки Відповідь: (2; 5). Відповідь: (-20; 6). Відповідь: (48; 8). Відповідь: (4; 2). Відповідь: (7; 3). Відповідь: (8; -6). Відповідь: (9; 3). Відповідь: (2; 3,8). 1035. Відповідь: (4; -4). Відповідь: (3; -1). Відповідь: (5; 4). Відповідь: (0,5; 4). Відповідь: (8; -1). Відповідь: (3; 5). 1036. Відповідь: (6; 3). Відповідь: (4; 2). Відповідь: (1; 2). Відповідь: (4; […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...
- Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...
- Розв’язування систем лінійних рівнянь методом додавання 1047. Відповідь: (7; -1). Відповідь: (3; 5). Відповідь: (4; -1/3). Відповідь: (-1; 10). Відповідь: (-1; 16). Відповідь: (2; -3). 1048. Відповідь: (4; -4). Відповідь: (2; 2). Відповідь: (1; 1). Відповідь: (2; -1). 1049. Відповідь: (8; 1). Відповідь: (1,2; 0). Відповідь: (-1; -2). Відповідь: (7; -1). Відповідь: (4; -1). Відповідь: (6; -2). Відповідь: u = 2, […]...
- Розв’язування задач за допомогою систем лінійних рівнянь Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 30. Розв’язування задач за допомогою систем Лінійних рівнянь Ми вже розглядали задачі, які можна розв’язати за допомогою рівнянь. Математичною моделлю задачі може бути не тільки рівняння, а й система рівнянь. Зазвичай це має відношення до тих задач, де невідомими є значення двох або більшої кількості величин. Приклад […]...
- Аналітичні способи розв’язування систем лінійних рівнянь із двома змінними Розв’яжіть задачі 1121. 1) х = 2y + 3; 2); х = -3у – 9; 3) х = 2у – 2,5; 4) х = 2y – 3. 1122. 1) у = 15 – 5х; 2) у = 4х + 6; 3) у = 6 – 2х; 4) у = 2 + 1,5х. 1123. 1) 2y […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...
- Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...
- АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &24. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, що систему лінійних рівнянь із двома змінними можна розв’язати графічно. Проте існують інші, більш точні способи розв’язування таких систем – аналітичні способи. У цьому параграфі ви дізнаєтесь про два з них. До аналітичних способів розв’язування […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: сформувати вміння складати системи рівнянь за умовою задачі; домогтися засвоєння схеми розв’язання задачі за допомогою системи лінійних рівнянь з двома змінними; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати вміння грамотно формулювати власні думки; – виховна: виховувати позитивне ставлення до навчання, старанність, спостережливість; Тип уроку : засвоєння нових знань, умінь, навичок. […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...
- Розв’язування показникових рівнянь і систем УРОК 47 Тема. Розв’язування показникових рівнянь і систем Мета уроку. Формування умінь учнів розв’язувати показникові рівняння і системи різними способами. І. Перевірка домашнього завдання. Три учні відтворюють на відкидних дошках розв’язування вправ: 1 учень – № 34 із “Запитань для повторення”; 2 учень – № 1 (12-14); 3 учень – № 1 (15, 16). У […]...
- Розв’язання задач за допомогою систем рівнянь 973. Нехай 1 кг помідорів коштує x грн, а 1 кг огірків – у грн. Складаємо систему рівнянь: Відповідь: 3 грн.; 2 грн. 974. Нехай 1 альбом коштує x грн., а 1 зошит у грн. Складаємо систему рівнянь: Відповідь: альбом коштує 4 грн., зошит – 1 грн. 975. Нехай маса 1 ящика слив x кг, […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Розв’язування показникових рівнянь і систем показникових рівнянь УРОК 48 Тема. Розв’язування показникових рівнянь і систем показникових рівнянь Мета уроку. Формування уміння розв’язувати показникові рівняння і системи показникових рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування вправи № 1 (25, 28, 30, 46). 2. Усне розв’язування показникових рівнянь за допомогою таблиці 20 для усних обчислень “Показникові рівняння” 1 2 3 4 […]...
- Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...