Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання
Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
& 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання
Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише одну змінну.
Приклад 1. Розв’язати систему рівнянь:
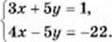
Р о з в ‘ я з а н н я. У даній системі коефіцієнти
7х = -21.
Додавання рівнянь системи, яке ми застосували, називають почленим додаванням. Замінимо одне з рівнянь системи (1), наприклад перше, рівнянням 7х = 21. Матимемо систему:
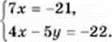
З першого рівняння системи (2) маємо: х = -3. Підставивши це значення в друге рівняння системи (2), одержимо, що у = 2.
Отже, пара чисел (-3; 2) є розв’язком системи (2). Переконаємося, що ця пара чисел
Отже, системи (1) і (2) мають один і той самий розв’язок, тому є рівносильними.
В і д п о в і д ь: (-3; 2).
Способом додавання зручно розв’язувати системи, у рівняннях яких коефіцієнти при одній і тій самій змінній є протилежними числами.
Будь-яку систему лінійних рівнянь з двома змінними можна звести до вигляду, який буде зручним для застосування способу додавання. Розглянемо це па прикладі.
Приклад 2. Розв’язати систему 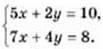
Розв’язання. Рівняння цієї системи не містять протилежних коефіцієнтів при однакових змінних, тобто вигляд системи не є зручним для застосування способу додавання. Але якщо помножити обидві частини першого рівняння на число -2, то коефіцієнти при змінній у в обох рівняннях стануть протилежними. Після чого можна почленно додати рівняння системи.
Запишемо це розв’язання:
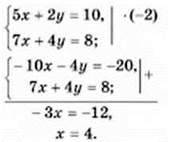
Підставимо знайдене значення х в друге рівняння системи, щоб знайти у. Маємо: 7 ∙ 4 + 4у = 8, звідки у = -5.
Остаточно маємо: 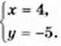
В і д п о в і д ь: (4; -5).
Послідовність дій, якої слід дотримуватися, розв’язуючи систему лінійних рівнянь з двома змінними способом додавання, розглянемо па прикладі системи 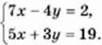
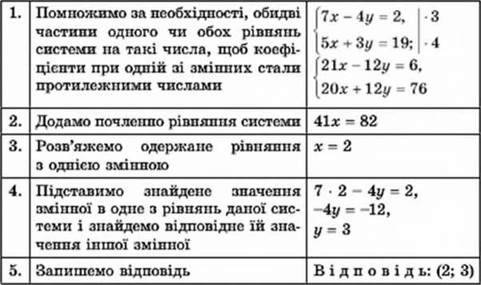
Якої послідовності дій слід дотримуватися, розв’язуючи систему двох лінійних рівнянь з двома змінними способом додавання?
1054. (Усно) Яке рівняння одержимо, якщо почленно додамо рівняння системи:

1055. (Усно) На яке число треба помножити обидві частини першого рівняння системи, щоб у рівняннях коефіцієнти при змінній у стали протилежними:

1056. На яке число треба помножити обидві частини першого рівняння, щоб у рівняннях коефіцієнти при змінній х стали протилежними:
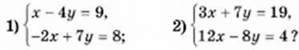
1057. (Усно) Яким зі способів (підстановки чи додавання) зручніше розв’язувати систему:
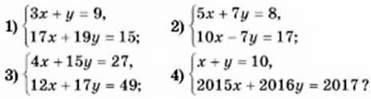
1058. Розв’яжіть систему рівнянь способом додавання:
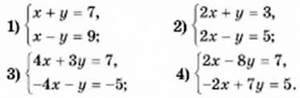
1059. Розв’яжіть систему рівнянь способом додавання:
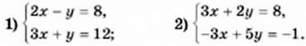
1060. Розв’яжіть систему рівнянь способом додавання:

1061. Знайдіть розв’язок системи рівнянь способом додавання:

1062. Знайдіть розв’язок системи рівнянь способом додавання:

1063. Розв’яжіть систему рівнянь способом додавання:

1064. Розв’яжіть систему рівнянь:
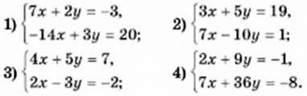
1065. Розв’яжіть систему рівнянь.

1066. Знайдіть розв’язок системи способом додавання:
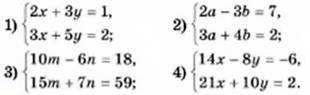
1067. Знайдіть розв’язок системи способом додавання:
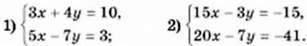
1068. Розв’яжіть систему рівнянь:

1069. Розв’яжіть систему рівнянь:
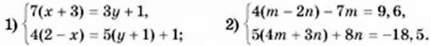
1070. Складіть рівняння прямої, графік якої проходить через точки:
1) А(4; -4) і В( 12; -1);
2) М(-3; 6) і N(9; -2).
1071. Графік лінійної функції проходить через точки (- 4; 5) і (12; 1). Задайте цю функцію формулою.
1072. Розв’яжіть систему рівнянь:
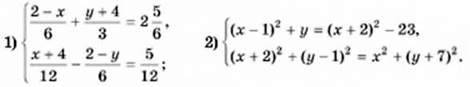
1073. Розв’яжіть систему рівнянь:
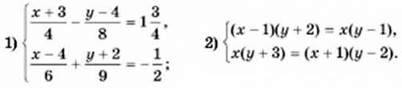
1074. Чи має система рівнянь розв’язки і скільки.
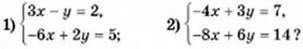
Вправи для повторення
1075. Чи належать графіку функції у = -4,5х + 1 точки:
А(-2; 10),
В(0; -1),
С(4; 17),
D(10; -44)?
1076. Пара чисел (-2; -3) є розв’язком системи рівнянь:
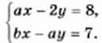
Знайдіть а і b.
1077. Які одночлени треба записати замість зірочки, щоб утворилася тотожність:
1) (7m – *)2 = * – * + 25а8;
2) (* + *)2 = 36р4 + * + 121b2;
3) (3р + *)2 = * + 24р*m7 + *;
4) (* – *)2 = * – 32mn2 + 16n4.
Цікаві задачі для учнів неледачих
1078. Чи існують такі цілі числа х і у, для яких виконується рівність х2 + 2018 = у2?