Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Розв’язування задач за допомогою лінійних рівнянь. Рівняння як математична модель задачі

Розв’язування задач за допомогою лінійних рівнянь. Рівняння як математична модель задачі

Урок № 8

Тема. Розв’язування задач за допомогою лінійних рівнянь. Рівняння як математична модель задачі

Мета: розкрити технологію розв’язування текстових задач на знаходження невідомих доданків за сумою з допомогою рівнянь як математичної моделі.

Тип уроку: систематизація знань, застосування вмінь.

Хід уроку

I. Перевірка домашнього завдання

Виконуємо перевірку, зібравши зошити й оцінивши письмові роботи учнів.

II. Робота з випереджальним домашнім завданням

@ Взагалі, про використання рівнянь для розв’язування

задач говорилося раніше.(У 5 класі цьому було присвячено серію завдань, а потім у 6 класі в темі “Рівняння” та в інших темах розв’язування задач за допомогою рівнянь уже обговорювалося.)

Тому в роботі з випереджальним домашнім завданням слід акцентувати учнів на тому, що:

1) цю задачу можна було б розв’язати і за діями, але простіше скласти рівняння (більш зрозумілим буде розв’язання);

2) розв’язування задачі починається з того, що з’ясовують, які числа невідомі, і вибирають, яке з них (зазвичай це найменше з невідомих) по значити буквою (цьому етапу в поясненнях відповідає перше речення:

“Нехай х…”);

3) після вибору й позначення невідомого використовують умову задачі (співвідношення між невідомими та відомими величинами), щоб скласти рівняння (цьому етапу в поясненні до розв’язування задачі відповідає текст, що починається зі слів: “Тоді…” і закінчується “…маємо рівняння”);

4) розв’язання рівняння є лише одним з кількох етапів розв’язання задачі (і на цьому також слід акцентувати учнів), причому розв’язанням рівняння не закінчується розв’язання задачі;

5) останньою частиною розв’язання задачі за допомогою рівняння є пояснення (інтерпретація) знайдених у ході розв’язування рівняння чисел (частина тексту, що починається зі слів: “Отже,…”).

Наведені міркування можуть стати результатом або призведуть до того, що учні, виконавши певні дії з текстом, що дається їм для домашньої роботи, здобудуть такий результат:

У двох цистернах зберігається 66 т бензину, причому в першій бензину в 1,2 рази більше, ніж у другій. Скільки бензину в кожній цистерні?

Розв’язання

Нехай у другій цистерні х т бензину (І), тоді в першій – 1,2х т.

У двох цистернах разом (х + 1,2х) т бензину, що за умовою дорівнює 66 т. Маємо рівняння:

Х + 1,2х = 66, (II)

2,2х = 66, (III)

Х = 66 : 2,2,

Х = 30.

Отже, у другій цистерні було 30 т бензину, а в першій 1,2 – 30 = 36 (т). (IV)

Відповідь. 36 т; 30 т.

І. Невідоме позначаємо буквою.

II. Використовуючи умову задачі, складаємо рівняння.

III. Розв’язуємо рівняння.

IV. Пояснення (інтерпретація знайдених коренів відповідно до умови задачі)

III. Систематизація знань

@ Після розбору випереджального домашнього завдання в основному робота з систематизації знань виконана. (План розв’язання задач за допомогою рівнянь, що склали в ході роботи з випереджальним домашнім завданням, учні записують у зошити). Але є ще два моменти, на які треба обов’язково звернути увагу:

1) рівняння є лише математичною моделлю задачі, тобто показує співвідношення між числовими значеннями величин, про які йдеться в задачі;

2) останній етап у ході розв’язування задач – інтерпретація знайдених коренів рівняння відповідно до умови задачі – є необхідним, бо можливий варіант, коли корінь рівняння, складеного за умовою задачі, не відповідає змісту задачі (див. нижче № 6).

IV. Застосування вмінь

Виконання усних вправ

Запишіть рівняння, що відповідає умові задачі:

1) сума двох чисел дорівнює 50, одне число х, а друге – у 4 рази менше;

2) сума двох чисел дорівнює 50, одне на 30 менше від іншого;

3) сума двох чисел дорівнює 50, одне становить 40 % від іншого;

4) сума двох чисел дорівнює 50, одне з них становить 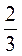іншого;

5) сума трьох чисел дорівнює 50, одне з них на 10 більше від другого, а третє в 2 рази більше за друге.

Виконання письмових вправ

1. Бригада робітників за два тижні виготовила 356 деталей, причому за другий тиждень було виготовлено в 3 рази більше деталей, ніж за перший. Скільки деталей було виготовлено за перший тиждень?

@ Перед розв’язуванням задачі важливо, щоб учні здійснили порівняння умови даної задачі із задачею, розібраною в попередньому пункті і, здійснивши порівняння, з’ясували, які спільні і відмінні риси мають умови задач, і звідси вийшли на спосіб розв’язування задачі (за планом, складеним під час розбору випереджального домашнього завдання).

2. Дріт довжиною 456 м розрізали на 3 частини, причому перша частина в 4 рази більша від третьої, а друга – на 114 м довша за третю. Знайдіть довжину кожної частини.

@ Так само, як і перед розв’язуванням задачі №1, порівняємо умову №2 з №1 і з’ясуємо, чим відрізняється умова №2 від №1 (кількість невідомих величин більша на одиницю) і чим схожі ці задачі (як і в №1, відома сума всіх невідомих величин). Після цього за планом розв’язуємо задачу.

3. Одна сторона трикутника в 3 рази менша від другої і на 2,3 дм менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 10,8 дм.

4. За 3 ручки і 5 олівців заплатили 3 грн. 16 к. Скільки коштує одна ручка й один олівець, якщо олівець дешевший від ручки на 98 к?

5. За три дні турист пройшов 128 км, причому другого дня він подолав 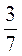відстані, яку пройшов за перший день, а третього – 40 % того, що за перший. Скільки кілометрів проходив турист щодня?

@ Порівнюючи, звернути увагу на те, що в цій задачі дві невідомі величини виражаються як частина від третьої, і тому, на відміну від розв’язування попередніх задач, за х буде простіше позначити саме ту невідому величину, через яку виражаються дві інші.

6. Чи можна розставити 158 книжок на трьох полицях так, щоб на першій полиці було на 8 книжок менше, ніж на другій, і на 5 книжок більше, ніж на третій?

@ Принципово нова задача. По-перше, формулювання питання (оскільки учні не знайомі зі схемою доведення “від супротивного”), по-друге, тому що в цій задачі учні вперше зустрічаються з випадком, коли корінь рівняння не задовольняє умову задачі. Тому цю задачу треба ретельно обговорити й пояснити учням, що зміст питання “Чи може виконуватись якесь твердження?” в математиці з’ясовується так: “Припустимо, що може, і подивимось, чи буде це відповідати дійсності”.

Щоб встигнути розібрати таку велику кількість задач, можна організувати роботу учнів таким чином: оскільки основна мета – формування вмінь формалізувати умову задачі та складати рівняння як математичну модель задачі, то для № 1-5 можна скласти рівняння, а розв’язування рівнянь залишити для домашньої роботи.

V. Підсумки уроку

Один з варіантів – запропонувати учням узагальнити тип задач, що були розв’язані на уроці (знаходження доданків за відомою сумою).

VI. Домашнє завдання

№ 1. Розв’яжіть рівняння до задач № 1-5 (класна робота).

№ 2. У магазин завезли 425 кг картоплі, яку було продано за два дні, причому за перший день було продано в 4 рази більше картоплі, ніж за другий. Скільки картоплі було продано за третій день?

№ 3. Три 7-мі класи посадили разом 56 дерев. 7-Б клас посадив 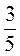числа дерев, що посадив 7-А клас, а 7-В – 120 % того, що посадив 7-А клас. Скільки дерев посадив кожний клас?

№ 4. Чи можна 59 банок консервів розкласти в три ящики так, щоб у третьому було на 9 банок більше, ніж у першому, а в другому – на 4 банки менше, ніж у третьому?