Розв’язування задач за допомогою рівнянь
Урок № 104
Тема. Розв’язування задач за допомогою рівнянь
Мета: вдосконалити вміння розв’язувати задачі складанням рівняння; відпрацювати навички розв’язування лінійних рівнянь з однією зміною та виконання арифметичних дій з раціональними числами.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
@ Часто-густо учні, особливо на початку вивчення теми припускаються певних помилок під час складання таблиць, рівнянь та запису пояснень до них,
Також хотілося б звернути увагу на можливі різні варіанти складання рівняння (коли за невідоме число беруть не меншу, а більшу величину). Слід пояснити учням, що з двох варіантів складання рівняння зазвичай обирають той, в якому за х позначено меншу з величин.
III.
Усні вправи
1. Обчисліть: | А) |
| Б) |
| В) |
|
2. За рисунком складіть задачу, щоб її розв’язання привело до рівняння 2х + 6х = 32. Розв’яжіть задачу:

3. Дано 2 числа а і b. Запишіть у вигляді рівності:
А) що сума цих чисел 12;
Б) різниця цих чисел 3;
В) число а на 2 більше від числа b;
Г) число а на 3 менше від числа b;
Д) подвоєне число а дорівнює потроєному числу b.
IV. Вдосконалення вмінь
@ Останній урок розділу “Розв’язування задач за допомогою рівнянь” присвячений розв’язуванню задач, які умовно можна назвати так: “Було, змінилось, стало”.
Автор пропонує розв’язання таких задач також починати зі складання таблиці. Звертаємо увагу на те, що традиційно складним для учнів є розуміння того, як скласти рівність за умови, що один вираз у а разів більший (менший) від іншого.
Задача 1. У великому бідоні втричі більше молока, ніж у малому. Коли у великий бідон долили 6 л молока, а в малий – 7 л, то у великому бідоні молока стало вдвічі більше, ніж у малому. Скільки молока було в кожному бідоні спочатку?
Задача 2. В одному баку 400 л бензину, а у другому – 900 л. Кожну годину з першого бака виливають 20 л бензину, а з другого – 10 л. Через скільки годин у першому баку залишиться бензину в 4 рази менше, ніж у другому?
Задача 3. У Василька з Марічкою було порівну грошей. Коли Василько купив книжку за 14 гривень, а Марічка ляльку за 6 гривень, то в дівчинки залишилось грошей у 3 рази більше, ніж у хлопчика. Скільки грошей було в кожного з них спочатку?
Задача 4. В одному ящику було в 7 разів більше апельсинів, ніж у другому. Коли з першого ящика взяли 38 апельсинів, а з другого – 14, то в другому залишилося на 87 апельсинів менше, ніж у першому. Скільки апельсинів було в кожному ящику спочатку?
Додаткова вправа
Розв’яжіть рівняння:
А) 0,3(6 – 3у) = 4,5 – 0,8(у – 9);
Б) 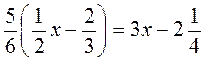 .
.
V. Підсумки уроку
Яке з рівнянь відповідає умові задачі: “У першій шафі було у 4 рази менше книжок, ніж у другій. Коли в першу шафу поклали 17 книжок, а з другої взяли 25, то в обох шафах книжок стало порівну. Скільки книжок було в кожній шафі спочатку?”
(За х позначимо початкову кількість книжок у першій шафі.)
А) х + 25 = 4х – 17; б) х + 17 = 4х – 25; в) х + 17 = х – 25; г) 4х + 17 = х – 25.
VI. Домашнє завдання
1. У двох кошиках було порівну яблук. Після того, як із першого кошика взяли 50 яблук, а з другого – 90, у першому яблук стало втричі більше, ніж у другому. Скільки яблук було в кожному кошику спочатку?
2. У книжковій шафі було в 6 разів більше книжок, ніж на етажерці. Після того як з шафи взяли 46 книжок, а з етажерки – 18, на етажерці залишилось на 97 книжок менше, ніж у шафі. Скільки книжок було спочатку у шафі та скільки на етажерці?
3. Обчисліть:  .
.


