СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ
РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
&23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ
Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад.
Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного другого числа дорівнює 11. Знайдіть ці числа.
Розв’язання. У задачі два невідомі числа. Нехай перше число дорівнює х, а друге – у. Сума цих чисел дорівнює 3,
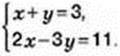
Дістали систему двох лінійних рівнянь із двома змінними. Якщо дібрати таку пару чисел (х; у), яка задовольнятиме обидва рівняння системи, то систему буде розв’язано. Застосувавши спосіб перебору, отримаємо пару чисел (4; -1), яка задовольняє
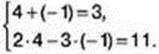
Отже, одним із шуканих чисел є число 4, а другим – число -1.
Запам’ятайте!
Розв’язком системи двох лінійних рівнянь із двома змінними називають таку пару чисел (х; у), яка одночасно є розв’язком кожного рівняння системи. Розв’язати систему рівнянь – означає знайти всі її розв’язки або встановити, що розв’язків немає.
У загальному вигляді систему двох лінійних рівнянь із двома змінними записують так:
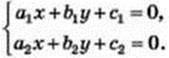
Розв’язуючи задачу 1, ми застосували спосіб перебору, який не завжди є зручним. Знайти потрібну пару чисел можна за допомогою графіків рівнянь системи. Координати точки перетину цих графіків є розв’язком системи. Такий спосіб розв’язування системи двох лінійних рівнянь із двома змінними називають графічним.
Подивіться на малюнок 75. Ви бачите, що в одній системі координат побудовано графіки рівнянь x + у = 3 і 2х – Зу = 11, які склали за умовою задачі 1. Ці прямі перетинаються в точці А(4; -1). Координати цієї точки одночасно є розв’язком і першого, і другого рівнянь системи
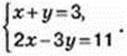
Отже, пара чисел (4; -1) є розв’язком цієї системи, а значить, вона дає відповідь і до самої задачі 1.
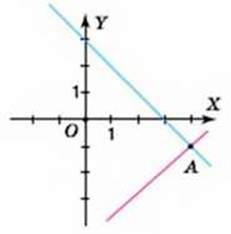
Мал. 75
Зверніть увагу:
Щоб розв’язати систему двох лінійних рівнянь із двома змінними графічним способом, треба:
1) в одній системі координат побудувати графік кожного з рівнянь системи;
2) визначити координати точки перетину цих графіків, якщо це можливо.
? Скільки розв’язків може мати система двох лілійних рівнянь із двома змінними? Поміркуємо, спираючись на графіки рівнянь системи.
Із курсу геометрії ви знаєте, що на площині дві прямі або перетинаються, або паралельні, або збігаються. Отже, для системи двох лінійних рівнянь із двома змінними можливі три випадки:
– система має єдиний розв’язок (мал. 76), якщо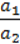 
≠ 
;
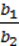– система не має розв’язків (мал. 77), якщо ≠ ≠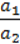 
;
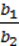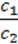– система має безліч розв’язків (мал. 78), якщо = = .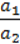
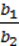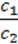Мал. 76
Задача 2. Розв’яжіть графічно систему рівнянь:
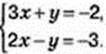
Розв’язання. У рівняннях системи відповідні коефіцієнти при х і у не пропорційні: 
≠ 
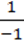, тому система має єдиний розв’язок. Зведемо рівняння системи до вигляду лінійної функції, розв’язавши кожне з них відносно у:
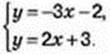
Для кожного рівняння системи визначимо дві точки, через які проходить його графік, склавши таблицю значень відповідної функції.
У = – 3х – 2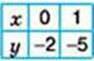
Y = 2x + 3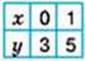
Мал. 77
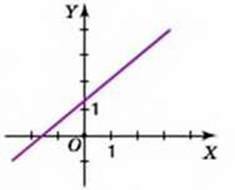
Мал. 78
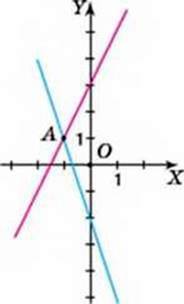
Мал. 79
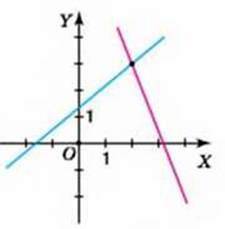
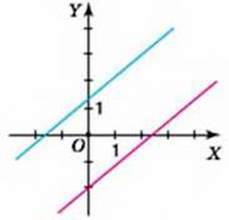
На координатній площині побудуємо графіки лінійних рівнянь:
3х + у = -2 через точки (0; -2) і (1; -5) та 2х – у = -3 через точки (0; 3) і (1; 5). Побудовані прямі (мал. 79) перетинаються в точці A(-1; 1). Отже, пара чисел (-1; 1) є шуканим розв’язком системи, заданої в умові задачі.
? Чи можна побудувати графік лінійного рівняння, не зводячи його до вигляду лінійної функції? Так. Можна визначити координати точок, що лежать на осях. Наприклад, для рівняння х – у = -2 це точки (0; 2) і (-2; 0).
Використання графічного способу розв’язування системи лінійних рівнянь із двома змінними, як і способу перебору, викликають певні утруднення: прямі не завжди зручно зображати в зошиті або складно точно визначити координати точки перетину. У наступному параграфі ви дізнаєтеся про інші способи розв’язування системи лінійних рівнянь із двома змінними.
Дізнайтеся більше
1 Володимир Йосипович Левицький (1872-1956) є “основоположником математичної культури нашого народу”, – так сказав про Володимира Левицького академік Михайло Кравчук. І мав на це всі підстави. Вважалося, що саме професор В. Й. Левицький першим написав українською мовою справжню фахову статтю з математики. Він був незмінним редактором першого українського наукового часопису з природничих наук, приділяв значну увагу згуртуванню математиків-українців для наукової роботи. Великою заслугою В. Левицького було те, що він зібрав і впорядкував матеріали з української математичної термінології, що була надрукована в 1903 р.
2. Задачі, що відповідають сучасним задачам на складання і розв’язування систем рівнянь із кількома змінними, зустрічаються ще у вавилонських і єгипетських рукописах II ст. до н. е., а також у працях давньогрецьких, індійських і китайських мудреців. У китайському трактаті “Математика в дев’яти книгах” у словесній формі викладено правила розв’язування систем рівнянь, описано деякі закономірності пошуку розв’язків. Книга була остаточно відредагована фінансовим чиновником Чжан Цаном (помер у 150 р. до н. е.) і була призначена для землемірів, інженерів, чиновників і торговців. У ній зібрано 246 задач.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке система двох лінійних рівнянь із двома змінними?
2. Що називають розв’язком системи двох лінійних рівнянь із двома змінними?
3. Що означає – розв’язати систему лінійних рівнянь із двома змінними?
4. Як розв’язати систему двох лінійних рівнянь із двома змінними графічним способом?
5. Скільки розв’язків може мати система двох лінійних рівнянь із двома змінними?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
1101. Перевірте, чи є розв’язком системи двох лінійних рівнянь із двома змінними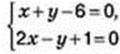 
пара чисел:
1) (1; 5); 2) (2; 4)?
1102. Назвіть розв’язок систем двох лінійних рівнянь із двома змінними за малюнками 80-82.
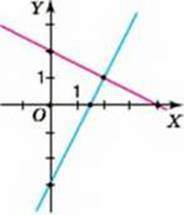
Мал. 80
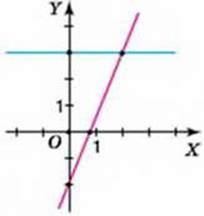
Мал. 81
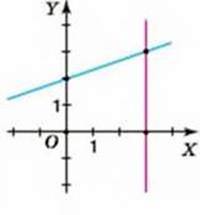
Мал. 82
1103. Перше рівняння системи має вигляд 3х – у + 5 = 0. Наведіть приклади коефіцієнтів другого рівняння системи, щоб система: 1) мала один розв’язок; 2) не мала розв’язків; 3) мала безліч розв’язків.
1104. Складіть систему двох лінійних рівнянь із двома змінними, якщо система:
1) не має розв’язків; 2) має безліч розв’язків.
1105. Складіть систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел:
1) (1; 3); 2) (-1; 2); 3) (0; 5); 4) (0; 0).
1106. Складіть систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел:
1) (2; 0); 2) (1; -2).
1107. Розв’яжіть графічно систему двох лінійних рівнянь із двома змінними:
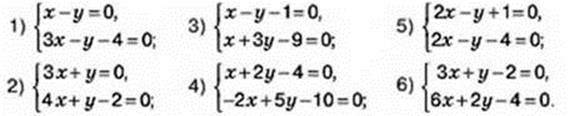
1108. Розв’яжіть графічно систему двох лінійних рівнянь з двома змінними:
1109. Знайдіть координати точки перетину графіків рівнянь:
1) 2х + у – 7 = 0 і 2х – у = 1; 2) 3х + у – 2 = 0 і х + 2у + 6 = 0.
1110. Знайдіть координати точки перетину графіків рівнянь: 2x + у – 1 = 0 і – х + у – 4 = 0.
1111. Розв’яжіть графічно систему рівнянь:
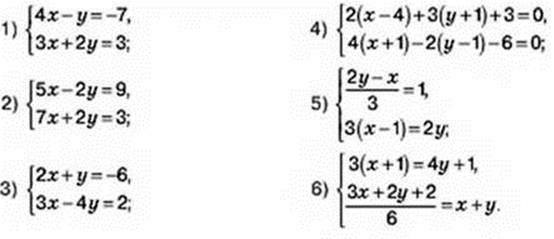
1112. Розв’яжіть графічно систему рівнянь:
1113. До рівняннях – у + 2 = 0 доберіть друге рівняння так, щоб отримана система двох лінійних рівнянь із двома змінними: 1) мала один розв’язок; 2) не мала розв’язків; 3) мала безліч розв’язків.
1114. До рівняння – х + у – 1 = 0 доберіть друге рівняння так, щоб отримана система двох лінійних рівнянь із двома змінними:
1) мала один розв’язок;
2) не мала розв’язків;
3) мала безліч розв’язків.
1115. За якого значення а прямі х – 2у = 4 і 2х + у = а перетинаються в точці, що лежить на осі:
1)абсцис; 2)ординат?
1116. Розв’яжіть графічно систему рівнянь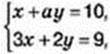 
якщо пара чисел (-2; 4) є розв’язком першого рівняння системи.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1117. Тетянка за 3 зошити і 2 ручки заплатила 16 грн, а Сергійко за ручку і 4 зошити – 13 грн. Скільки коштує зошит і скільки коштує ручка? Складіть систему двох лінійних рівнянь із двома змінними та розв’яжіть її графічно.
1118. Складіть задачу, подібну до попередньої задачі, та розв’яжіть її графічним способом.
ЗАДАЧІ НА ПОВТОРЕННЯ
1119. Туристи відправились у триденний похід. За перший день вони пройшли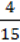 
усього шляху, за другии – 
решти, а за третій – останні 11 км. Який шлях подолали туристи за три дні?
1120. Розв’яжіть рівняння:
1) 
– 
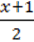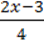= 2,5x;
2) 
– 
– 
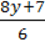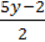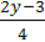= 3.
(1 votes, average: 5.00 out of 5)
Loading...