Співвідношення між тригонометричними функціями одного аргументу
УРОК 12
Тема. Співвідношення між тригонометричними функціями одного аргументу
Мета уроку: вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значень тригонометричних функцій за однією відомою функцією.
І. Аналіз контрольної роботи
II. Мотивація навчання
Дуже часто при розв’язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо задано лише значення однієї
III. Сприймання і усвідомлення нового матеріалу
1. Співвідношення між синусом і косинусом.
Нехай точка??(х, у) одиничного кола отримана поворотом точки Р0(1; 0) на кут? радіан, тоді згідно з означенням синуса і косинуса: х = cos?, у = sin? (рис. 100)
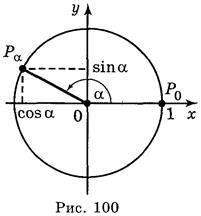
Оскільки точка Р?(х;у) належить одиничному колу, то координати (х; у) задовольняють рівнянню х2 + у2 = 1. Підставивши в це рівняння замість х і у значення cos? і sin?, отримаємо:
(cos?)2 + (sin?)2 = 1 або (враховуючи,
Таким чином, sin2 ? + cos2 ? = 1 для всіх значень?. Ця рівність називається основною тригонометричною тотожністю.
З основної тригонометричної тотожності можна виразити sin? через cos? і навпаки.
, 
.
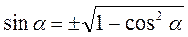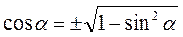Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
A) cos? = 
і sin? = ;
Б) sin? = – і cos? = –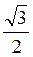
;
В) sin? = і cos? = – .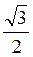
При одному і тому самому значенні??
Відповідь: а) ні; б) так; в) так.
2. Знайдіть cos?, якщо sin? = 0,6 і 
< ? < ?.
Відповідь: cos? = -0,8.
3. Знайдіть sin?, якщо cos? =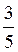 
і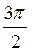 
< ? < 2?.
Відповідь: sin? = –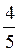
.
4. Спростіть вирази:
А) 1 + sin2 ? + cos2 ?;
Б) 1 – sin2 ? – cos2 ?;
В) 2sin2 ? + cos2 ? – 1;
Г) (1 – cos?)(1 + cos?);
Д)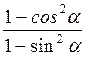 
;
Є) sin4 ? – cos4 ? + 1.
Відповідь: а) 2; 6) 0; в) sin2 ?; г) sin2 ?; д) tg2?; є) 2sin2?.
5. Доведіть тотожності:
А) (1 – cos 2?)(1 + cos 2?) = sin2 2?;
6) cos4 ? – sin4 ? = cos2 ? – sin2 ?;
В) (sin2 ? – cos2 ?)2 + 2cos2? sin2? = sin4 ? + cos4 ?;
Г) 2cos2? sin2? + cos4? + sin4? = 1;
Д) sin6 ? + cos6 ? = 1 – 3sin2? cos2?;
Є)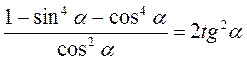 
.
6. Знайдіть cos?, якщо cos4 ? – sin4 ? =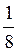 
.
Відповідь: cos? = ±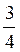
.
2. Співвідношення між тангенсом і котангенсом. Згідно з визначенням тангенса і котангенса,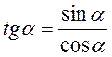 
, 
.
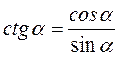Перемноживши ці рівності, одержимо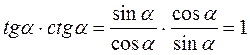 
Отже, tg? – ctg? = 1 для всіх значень?, крім? = , k, k
?. із одержаної рівності можна виразити tg? через ctg? і навпаки: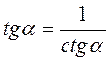 
; 
.
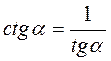Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
A) tg? =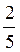 
і ctg? = 
;
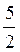Б) tg? = 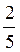і ctg? = ;
В) tg? = – і ctg? = 2
При одному і тому самому значенні??
Відповідь: а) так; б) ні; в) ні.
2. Знайдіть
А) tg?, якщо ctg? =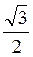 
;
Б) ctg?, якщо tg? = -1;
В) tg?, якщо ctg? = 0.
Відповідь: а)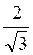 
; б) -1; в) не існує.
3. Дано: х = 2tg?, у = ctg?. Знайдіть ху.
Відповідь: ху =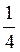 
.
4. Дано tg? + сtg? = 2. Знайдіть tg 2 ? + сtg2 ?.
Відповідь: 2.
5. Спростіть:
А) tg? – сtg? – 1;
Б) sin2 ? – tg? – сtg?;
В) tg 1° – tg 3° – tg 5° – … – tg 89°.
Відповідь: а) 0; б) – соs?; в) 1.
6. Доведіть тотожності:
А) (tg? + сtg?)2 – (tg? – сtg?)2 = 4;
Б)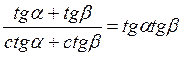 
;
В)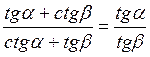 
;
Г)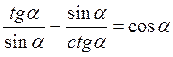 
;
Є) 4 + (сtg? – tg?)2 = (сtg? + tg?)2.
3. Співвідношення між тангенсом і косинусом, котангенсом і синусом.
Розділимо ліву і праву частину рівності sіn2 ? + соs2 ? = 1 на соs2?, вважаючи, що соs2? ? 0, одержимо:
; 
,
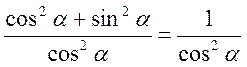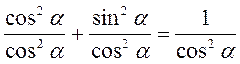Звідси: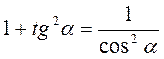 
, де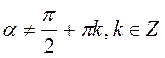 
.
Розділимо ліву і праву частину рівності sіn2 ? + соs2 ? = 1 на sіn2 ?, вважаючи, що sіn? ? 0, одержимо
; 
,
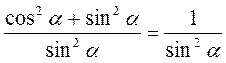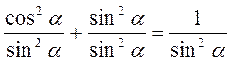Звідси: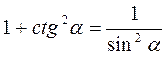 
, де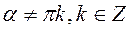 
.
Виконання вправ______________________________
1. Чи можуть бути справедливими одночасно рівності.
А) tg? = 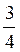і соs? = ;
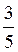Б) сtg? = 1 і sіn? =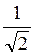 
;
В) tg? = 
і sіn? =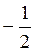 
при одному і тому ж значенні??
Відповідь: а) ні; б) так; в) ні.
2. Відомо, що tg? = 2 і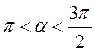 
. Знайдіть sіn?, соs? і сtg?.
Відповідь: sіn? =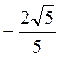 
; соs? = 
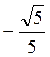; сtg? = .
3. Відомо, що sіn? = 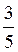і 0 < ? < . Знайдіть соs?, tg?, сtg?.
Відповідь: соs? = 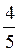; tg? = 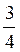; сtg? = 
.
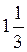4. Відомо, що сtg? = -3 і? – кут IV чверті. Знайдіть sіn?, соs?, tg?.
Відповідь: sіn? =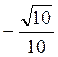 
; соs? = 
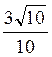; tg? = 
.
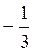5. Відомо, що соs? =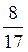 
і? – кут І чверті. Знайдіть sіn?, tg?, сtg?.
Відповідь: sіn? =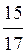 
; tg? = 
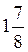; сtg? = 
.
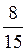6. Спростіть вираз:
А)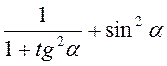 
;
Б)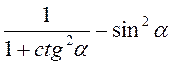 
;
В)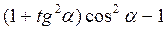 
;
Г)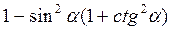 
;
Д)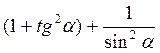 
;
Є)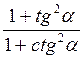 
.
Відповідь: а) 1; б) 0; в) 0; г) 0; д)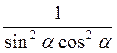 
; є) tg?.
7. Доведіть тотожності:
А)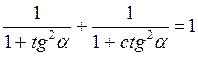 
;
Б) (1 – сtg?)2 + (1 + сtg?)2 =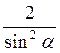 
;
В)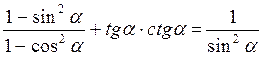 
;
Г)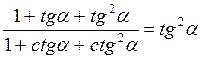 
.
III. Підведення підсумків уроку
IV. Домашнє завдання
Розділ І § 8. Запитання і завдання для повторення до розділу І № 56-58. Вправи № 40 (1; 2; 4; 10), № 44 (1; 2).
(1 votes, average: 5.00 out of 5)
Loading...