Текстові задачі

Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ

§ 12. Текстові задачі

Розглянемо основні види текстових задач.

Задачі на рух. Уже багато разів розв’язували задачі на рух і знаємо формулу шляху

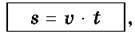
Що виражає взаємозв язок величин: s – пройдений шлях; v – швидкість руху, тобто відстань, яку проходять за одиницю часу; t – час руху.

Також знаємо формули, за якими можна знайти швидкість, якщо відомі пройдена відстань та час руху:

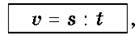
Та час, якщо відомі

пройдена відстань та швидкість:

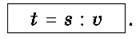
Зауваження: 1. У задачах на рух будемо вважати, що швидкість руху на всьому шляху не змінювалася.

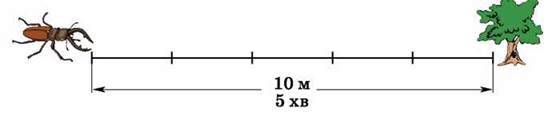
2. Одиниці вимірювання швидкості (км/год, м/хв, м/с тощо) залежать від умови задачі. Якщо, наприклад, жук за 5 хв проповзає 10 м, то його швидкість 10 : 5 = 2 (м/хв).

Розглянемо тепер, як розв’язуються задачі на рух по річці. У цих задачах є своя особливість: потрібно розрізняти швидкість руху за течією та швидкість руху проти течії.

Нехай, наприклад, власна швидкість човна (тобто його швидкість у стоячій воді) дорівнює 15

км/год, а швидкість течії річки дорівнює 2 км/год. Тоді швидкість, з якою човен пливе за течією, складається з його власної швидкості та швидкості течії: 15 + 2 = 17 (км/год). А швидкість, з якою човен пливе проти течії, отримуємо відніманням швидкості течії від власної швидкості човна: 15 – 2 = 13 (км/год).

Розглянемо задачі, у яких діють два учасники руху.

Рух з одного пункту з відставанням. Нехай два об’єкти одночасно починають рух в одному напрямі з однієї точки з різними швидкостями v1 = 5 км/год і v2 = 3 км/год.

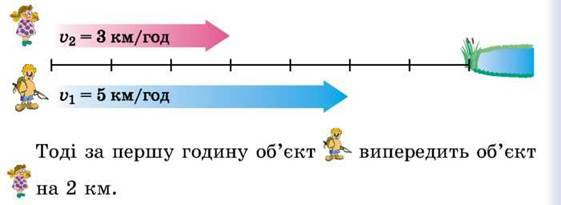
Відстань, на яку віддаляються об’єкти за одиницю часу, називається швидкістю віддалення vвід

У випадку руху з одного пункту з відставанням vвід = v1 – v2 (якщо v1 > v2).

Через t год між об’єктами буде відстань

Sвід = vвід ∙ t = (v1 – v2)t.

Задача 1. Два автомобілі одночасно виїхали в одному напрямі. Швидкість першого автомобіля 60 км/год, швидкість другого 72 км/год. Яка відстань буде між автомобілями через 9 год?

Розв’язання. vвід = (72 – 60) ∙ 9 = 12∙9 = 108 (км).

Рух з одного пункту в протилежних напрямах. Нехай два об’єкти одночасно починають рух з однієї точки в протилежних напрямах зі швидкостями v1 = 5 км/год і v2 = 3 км/год.

Тоді за першу годину об’єкт віддаляється від об’єкта на 8 км. У цьому випадку швидкість віддалення vвід = v1 + v2.

Через t год між об’єктами буде відстань sвід = vвід ∙ t = (v1 + v2)t.

Задача 2. Дві черепахи одночасно почали рухатись у протилежних напрямах зі швидкостями 6 дм/хв і 4 дм/хв. Яка буде відстань між черепахами через 35 хв?

Розв’язання. sвід = (6 + 4) ∙ 35 = 10 ∙ 35 = 350 дм.

Рух двох об’єктів назустріч один одному. Нехай два об’єкти одночасно починають рух назустріч один одному зі швидкостями v1 = 5 км/год і v2 = 3 км/год, причому початкова відстань між об’єктами більша за 8 км.

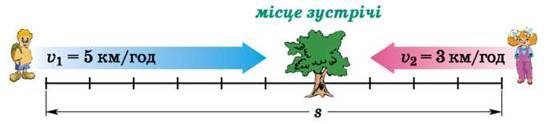
Тоді за першу годину відстань між об’єктами скоротиться на 8 км.

Відстань, на яку зближаються об’єкти за одиницю часу, називається швидкістю зближення vзбл.

У випадку руху двох об’єктів назустріч один одному vзбл = v1 + v2.

Якщо початкова відстань між об’єктами дорівнює s кілометрів і об’єкти зустрілися через tзуст, год, то очевидно, що

S = vзбл ∙ tзуст = (v1 + v2)t.

Якщо t < tуст, то через t год відстань між об’єктами скоротиться на відстань

S = vзбл ∙ t = (v1 + v2)t.

Задача 3. Два автобуси виїхали одночасно з двох міст і зустрілися через 5 год. Швидкість одного 45 км/год, а другого на 10 км/год більша. Знайди відстань між містами.

Розв’язання. 1) 45 + 10 = 55 (км/год) – швидкість другого автобуса; 2) (45 + 55) ∙ 5 = 500 (км) – відстань між містами.

Рух в одному напрямі навздогін. Нехай два об’єкти одночасно починають рух з різних точок в одному напрямі зі швидкостями v1 = 5 км/год іv2 = = 3 км/год, причому об’єкт, що має більшу швидкість, рухається позаду і початкова відстань між об’єктами більша за 2 км.

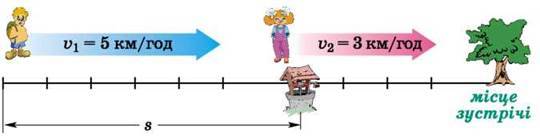
Тоді за першу годину об’єкт стане ближче до об’єкта на 2 км. У цьому випадку vзбл = v1 – v2 (якщo v1 > v2). Якщо початкова відстань між об’єктами дорівнює s км і об’єкт наздогнав об’єкт через tзуст год, то очевидно, що s = vзбл ∙ tзуст = (v1 – v2) tзуст.

Якщо t < t. то через t год відстань між об єктами скоротиться на відстань s = vзбл ∙ t = (v1 – v2)t.

Задача 4. З двох пунктів, відстань між якими 120 км, одночасно почали рух в одному напрямі пішохід зі швидкістю 5 км/год і автобус, який наздоганяв пішохода. Знайди швидкість автобуса, якщо він наздогнав пішохода через 2 год.

Розв’язання. vзбл = s : t; vзбл = 120 : 2 = 60 (км/год). Тоді швидкість автобуса дорівнює 60 + 5 = 65 (км/год).

Задачі, пов’язані з вартістю товару

Задача 5. Один кілограм цукерок коштує 25 грн. Скільки коштують 3 кг цукерок?

Розв’язання. 25 ∙ 3 = 75 (грн.). У цій задачі, як і в задачах на рух, маємо залежність між трьома величинами: вартість товару, його ціна та кількість.

Нехай С – вартість товару, a – його ціна (тобто вартість одиниці товару – 1 штуки, 1 м, 1 кг, 1 л тощо), а n – кількість товару у вибраних одиницях. Тоді

C = a ∙ n.

Отриману рівність називають формулою вартості. Вона означає, що

Вартість товару дорівнює ціні, помноженій на кількість товару.

З формули вартості за правилом знаходження невідомого множника легко виразити величини а і n:

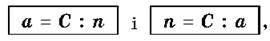
Тобто

Ціна товару дорівнює вартості, поділеній на кількість товару, а кількість товару дорівнює вартості, поділеній на ціну.

Задача 6. Літр соку коштує 12 грн. Скільки літрів соку можна купити за 48 грн.?

Розв’язання. 48 : 12 = 4 (л).

Задачі на роботу

Задача 7. Марія набрала на комп’ютері 9 сторінок за 3 год, а Тетяна – 8 сторінок за 2 год. Хто з дівчаток працював швидше?

Розв’язання. Марія набрала більше сторінок, ніж Тетяна, але вона й працювала більше часу. Для того щоб відповісти на питання задачі, треба знайти, скільки сторінок набрала кожна дівчинка за 1 год. Марія набирала по 9 : 3 = 3 сторінки за годину, а Тетяна – по 8 : 2 = 4 сторінки за годину. Отже, Тетяна працювала швидше, тому що за годину вона набрала більше сторінок.

Швидкість роботи ще називають продуктивністю. У такій задачі продуктивність праці Марії становить 3 сторінки за годину, а Тетяни – 4 сторінки за годину.

Якщо позначити буквою А – всю роботу, продуктивність – буквою N, а час роботи – t, то можемо записати рівність:

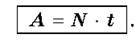
Ця рівність називається формулою роботи. Вона означає, що робота дорівнює продуктивності, помноженій на час роботи.

З формули роботи за правилом знаходження невідомого множника легко знайти величини N і t:

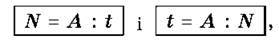
Тобто

Продуктивність дорівнює роботі, поділеній на час роботи, а час дорівнює роботі, поділеній на продуктивність.

Задача 8. Олеся миє 4 тарілки за 1 хв. Скільки тарілок помиє Олеся за 5 хв? Скільки потрібно часу, щоб Олеся помила 24 тарілки?

Розв’язання. За 5 хв Олеся помиє 4 ∙ 5 = 20 тарілок, а щоб помити 24 тарілки, їй потрібно 24 : 4 = 6 хв.

Початковий рівень

408. (Усно). 1) Хлопець з’ясував, що на шлях за течією річки було витрачено менше часу, ніж на той самий шлях проти течії. Чим це можна пояснити, якщо мотор човна працював однаково справно під час усієї подорожі? 2) На шлях по річці від пункту А до пункту В теплохід витратив 3 год, а на зворотний шлях – 2 год 30 хв. У якому напрямі тече річка?

Середній рівень

409. Знайди невідому величину.

Відстань,

140 км

120 км

750 м

570 м

Час, t

3 год

2 год

6 хв

5 с

Швидкість, v

28 км/год

32 км/год

95 м/с

12 м/с

410. Ціна книжки 35 грн. Яка вартість 2 книжок? 3 книжок? 5 книжок? 7 книжок? 12 книжок?

A = 35 грн. – стала	Ціна
Кількість (n), шт.	2	3	5	7	12
Вартість (C), грн.

411. Школярам мали закупити 80 ручок. Яка вартість покупки, якщо ціна однієї ручки 1 грн.?

2 грн.? 3 грн.? 4 грн.? 6 грн.?

N = 80 шт. – стала кількість
Ціна (а), грн.	1	2	3	4	6
Вартість (C), грн.

412. Бібліотека має закупити книжок на загальну суму 3600 грн. Скільки книжок зможе купити бібліотека, якщо ціна однієї книжки 10 грн.? 12 грн.?

15 грн.? 18 грн.? 20 грн.?

C = 3600 грн. – стала вартість
Ціна (а), грн.	10	12	15	18	20
Кількість (n), шт.

413. Ціна ручки 2 грн. Скільки таких ручок можна придбати за 50 грн.? 70 грн.? 90 грн.? 98 грн.? 106 грн.?

А = 2 грн. – стала ціна
Вартість (C), грн.	50	70	90	98	106
Кількість (n), шт.

414. Для нагородження призерів олімпіади купили 20 книжок з математики. Якою є ціна однієї книжки, якщо вартість покупки 600 грн.? 800 грн.?1000 грн.? 1200 грн.?

N = 20 шт. – стала кількість
Вартість (C), грн.	600	800	1000	1200
Ціна (а), грн.

415. Потрібно купити зошити на суму 30 грн. Якою є вартість одного зошита, якщо куплено 5 зошитів? 6 зошитів? 15 зошитів? 30 зошитів?

C = 30 грн. – стала кількість грошей
Кількість (n), шт.	5	6	15	30
Ціна (а), грн.

416. Принтер друкує з продуктивністю 7 сторінок за хвилину. Скільки сторінок він надрукує за 2 хв? 3 хв? 5 хв? 8 хв? 10 хв?

N = 7 сторінок за хвилину – стала продуктивність
Час (t), хв	2	3	5	8	10
Робота (А), стор.

417. Учень розв’язував задачі протягом 2 год. Скільки задач він розв’язав, якщо за годину розв’язував

3 задачі? 4 задачі? 5 задач? 7 задач? 8 задач?

T = 2 год – сталий час
Продуктивність (N), задач/год	3	4	5	7	8
Робота (А), задач

418. Студент має здати реферат на 48 сторінках. Скільки часу працюватиме студент над рефератом, якщо в день він буде робити 2 стор.? 3 стор.? 4 стор.? 6 стор.? 8 стор.?

А = 48 сторінок – стала робота
Продуктивність (N), стор./день	2	3	4	6	8
Час (t), днів

419. Майстер виготовляє 12 деталей за годину. За скільки годин він виготовить 36 деталей? 48 деталей? 60 деталей? 72 деталі? 120 деталей?

N = 12 дет./год – стала продуктивність
Робота (А), дет.	36	48	60	72	120
Час (t), год

420. Робітник працював 2 год. Якою є його продуктивність праці, якщо за ці 2 год він виготовив 12 деталей? 14 деталей? 18 деталей? 24 деталі? 26 деталей?

T = 2 год – сталий час
Робота (А), дет.	12	14	18	24	26
Продуктивність (N), дет./год

421. Книжка має 120 сторінок. Скільки сторінок за годину має читати учень, якщо хоче прочитати книжку за 4 год? 5 год? 8 год? 10 год?

A = 120 сторінок – стала робота
Час (t), год	4	5	8	10
Продуктивність праці (N), стор./год

422. 1) Один з автомобілів рухався 5 год зі швидкістю 72 км/год, а інший – 4 год зі швидкістю 85 км/год. Який з автомобілів проїхав більшу відстань? На скільки?

2) Один з велосипедистів за 4 год проїхав 56 км, а інший за 3 год проїхав 45 км. Який з велосипедистів мав більшу швидкість? На скільки?

3) Один з поїздів проїхав відстань 300 км зі швидкістю 75 км/год, а інший – відстань 204 км зі швидкістю 68 км/год. Який з поїздів витратив на дорогу менше часу? На скільки?

423. Склади задачі за коротким записом та розв’яжи їх.

Поїзд	Швидкість V, км/год	Час t, год	Відстань s, км
Товарний	42	6	Однакова
Пасажирський	?	4

Транспортний

Засіб

Швидкість V, км/год

Час t, год

Відстань s, км

Автомобіль

Однакова

Мотоцикл

424. Склади задачі за коротким записом і розв’яжи їх.

Учасник руху	Швидкість V, км/год	Відстань s, км	Час t, год
Велосипедист	15	60	Однаковий
Автомобіліст	?	296

Тварина	Швидкість V, км/год	Відстань s, км	Час t, год
Олень	12	36	Однаковий
Кінь	15	?

425. Швидкість катера в стоячій воді становить

14 км/год, а швидкість течії річки – 2 км/год. Визнач:

1) швидкість катера за течією річки;

2) швидкість катера проти течії річки;

3) шлях, який проходить катер за 2 год за течією річки;

4) шлях, який проходить катер за 3 год проти течії річки.

426. Визнач, яких рисунків стосуються формули (v1 > v2):

A) vзбл = v1 – v2; Б) vзбл = v1 + v2;

B) vвід = v1 – v2; Г) vвід = v1 + v2.

427. 1) Велосипедисти рухаються у протилежних напрямах. На скільки кілометрів вони віддаляться один від одного за 1 год? 2 год? 5 год?

2) Один з пішоходів наздоганяє іншого. На скільки кілометрів скоротить відстань цей пішохід через

1 год? 2 год? 5 год?

428. 1) Машини рухаються в одному напрямі. Яка буде відстань між ними через 1 год? 2 год? 7 год?

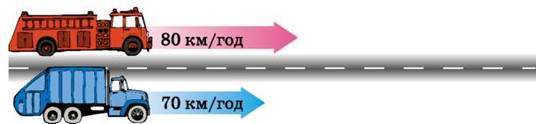
2) Велосипедисти рухаються назустріч один одному. На скільки кілометрів наблизяться вони один до одного за 1 год? 2 год? 4 год?

429. Від двох пристаней, відстань між якими 144 км, одночасно вийшли назустріч один одному два пароходи. Перший парохід плив зі швидкістю 25 км/год, другий – зі швидкістю 23 км/год. Через скільки годин вони зустрілись?

430. Від однієї пристані в протилежних напрямах вирушають два катери, швидкості яких відповідно

23 км/год та 28 км/год. Через який час відстань між ними дорівнюватиме 153 км?

431. Заповни таблицю.

Вартість (C), грн.	Ціна (а), грн.	Кількість (n), шт.
14	12
310	5
2040	120

432. Учень купив 8 зошитів по ціні 1 грн. 60 коп. та 3 ручки по ціні 2 грн. 20 коп. Яку здачу повинен отримати учень з купюри 20 грн.?

433. П’ять блокнотів дорожчі за п’ять ручок на 3 грн. Скільки коштує одна ручка, якщо ціна блокнота 3 грн. 90 коп.?

434. Один учень розв’язав 12 рівнянь за 2 год, а другий – 15 рівнянь за 3 год. У кого з учнів більша продуктивність праці і на скільки?

Достатній рівень

435. Катер, власна швидкість якого 18 км/год, плив

2 год за течією річки і 3 год проти течії. Яку відстань за цей час подолав катер, якщо швидкість течії річки 2 км/год?

436. Власна швидкість теплохода 22 км/год, а швидкість течії річки – 2 км/год. Скільки часу витрачає теплохід на шлях між двома пристанями, відстань між якими 120 км, якщо він буде пливти: 1) за течією; 2) проти течії?

437. Човен, власна швидкість якого 21 км/год, проплив річкою шлях від пункту A до пункту B і повернувся назад. Скільки часу витратив човен, якщо відстань між пунктами A і B становить 72 км, а швидкість течії – 3 км/год?

438. Склади умову задачі за рисунком. Розв’яжи задачу.

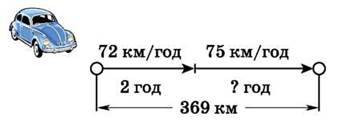
439. Склади умови задач за рисунками. Розв’яжи задачі.

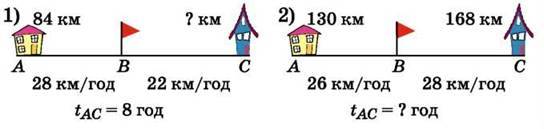
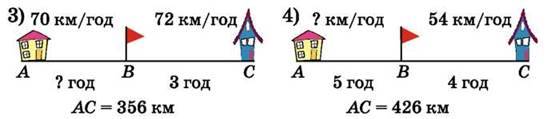
440. Два велосипедисти виїхали одночасно назустріч один одному з двох міст, відстань між якими 78 км. Велосипедисти зустрілися через 3 год. Знайди швидкість першого велосипедиста, якщо швидкість другого – 12 км/год.

441. Буратіно вийшов зі школи і пішов додому зі швидкістю 80 м/хв. Через 2 хв зі школи вийшов П’єро і пішов у тому самому напрямі зі швидкістю 100 м/хв. Через скільки хвилин після свого виходу П’єро наздожене Буратіно?

442. Відстань між містами A і B дорівнює 232 км. З міста B у бік, протилежний до A, вирушив велосипедист зі швидкістю 14 км/год. Одночасно з ним з міста A у тому самому напрямі вирушив мотоцикліст, який наздогнав велосипедиста через 4 год після початку руху. Знайди швидкість мотоцикліста.

443. Купили т кг картоплі по ціні 2 грн. за кілограм, після чого ще залишилося 15 грн. Напиши формулу для обчислення кількості грошей, які мали (познач її буквою Т). Обчисли Т, якщо m = 15.

444. Кожний з двох перших цехів підприємства виготовляє по а виробів за робочий день, а кожний з трьох наступних цехів – по b виробів за робочий день. Склади буквений вираз для обчислення кількості деталей, виготовлених на підприємстві за робочий день. Обчисли його значення, якщо а = 214, b = 210.

445. Майстер виготовляє 60 деталей за 4 год, а кожен з двох його учнів – по 18 деталей за 2 год. За скільки годин вони утрьох виготовлять 99 деталей?

Високий рівень

446. Відстань між пристанями 72 км. Власна швидкість човна становить 21 км/год. За який час подолає відстань між пристанями цей човен, рухаючись проти течії, якщо, рухаючись за течією, він подолав відстань за 3 год?

447. Перший автомобіль був у дорозі 6 год, другий – 3 год. Їхали вони з однаковою швидкістю. Перший автомобіль проїхав на 258 км більше, ніж другий. Яку відстань проїхав кожний автомобіль?

Розв’язання. Перший автомобіль рухався на 3 год довше і за цей час проїхав на 258 км більше. Оскільки швидкості автомобілів однакові, то їх можна знайти так: 258 : (6 – 3) = 86 км/год. Тоді перший автомобіль проїхав 86 – 6 = 516 км, а другий 86 – 3 = 258 км.

448. З Чигирина до Києва одночасно виїхали два автомобілі. Через 3 год відстань між ними була 24 км. Знайди швидкість другого автомобіля, якщо швидкість першого 85 км/год. Скільки випадків слід розглянути?

449. З міста M у місто N одночасно виїхали два автомобілі зі швидкостями 80 км/год та 85 км/год. Знайди відстань між містами M і N, якщо в момент прибуття другого автомобіля в місто N першому ще залишилося проїхати 15 км.

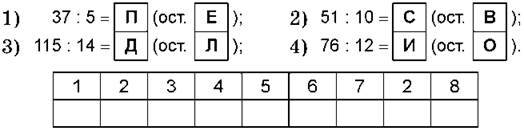
450. Вправи для повторення Заповни “віконця”. Знайди невідоме слово.