Головна ⇒ 📌Довідник з геометрії ⇒ Теорема синусів
Теорема синусів
Геометрія
Розв’язування трикутників
Теорема синусів
Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: 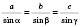 .
.
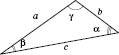
Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то
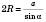 , або
, або 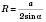 ,
,
де a – сторона трикутника, а  – протилежний цій стороні кут.
– протилежний цій стороні кут.
Теорема 3. У трикутнику проти більшого кута лежить більша сторона, проти більшої сторони лежить більший кут.
Ця теорема обгрунтовує твердження 2 (висновок), що наведене після теореми косинусів.
Дійсно, вид трикутника можна визначити, записавши теорему косинусів для його найбільшої сторони, тому що протилежний кут буде найбільшим. А якщо в трикутнику є прямий чи тупий кут, то він є найбільшим.
Related posts:
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Розв’язування задач на застосування теореми синусів УРОК № 8 Тема. Розв’язування задач на застосування теореми синусів Мета уроку: формування вмінь учнів застосовувати теорему синусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], посібник [14]. Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв’язування задач. Хід уроку І. Перевірка домашнього завдання 1. […]...
- Теорема синусів УРОК № 7 Тема. Теорема синусів Мета уроку: вивчення теореми синусів. Формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: формулюють теорему синусів та доводять її. Хід уроку І. Перевірка домашнього завдання Перевірити правильність виконання домашніх […]...
- Теорема косинусів УРОК № 4 Тема. Теорема косинусів Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її. Хід уроку I. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань […]...
- Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
- Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Наслідки теореми косинусів УРОК № 5 Тема. Наслідки теореми косинусів Мета уроку: виведення наслідків із теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів і наслідків з неї до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: застосовують теорему косинусів до розв’язування задач. Хід уроку І. […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Значення синусів і косинусів окремих кутів 10. Додатки 33. Значення синусів і косинусів окремих кутів...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Теорема, обернена до теореми Піфагора Урок № 35 Тема. Теорема, обернена до теореми Піфагора Мета: домогтися свідомого розуміння учнями змісту теореми Піфагора та її доведення: сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Формувати вміння відтворювати зміст вивченої теореми та застосовувати її під час розв’язування задач на доведення. Тип уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. […]...
- НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...
- Теорема Піфагора Урок № 34 Тема. Теорема Піфагора Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв’язування задач на знаходження невідомих сторін прямокутних трикутників. Типу уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання […]...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Основні задачі на розв’язування трикутників УРОК № 10 Тема. Основні задачі на розв’язування трикутників Мета уроку: ознайомити учнів з основними задачами розв’язування трикутників. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: описують основні випадки розв’язування трикутників та алгоритми їх розв’язування. Хід уроку І. Перевірка домашнього завдання Фронтальне опитування 1) […]...
- Формули косокутних трикутників 10. Додатки 36. Формули косокутних трикутників Теорема синусів: Теорема косинусів: Теорема тангенсів:...
- Розв’язання трикутників Геометрія Розв’язування трикутників Розв’язування трикутників Розв’язування трикутників полягає у знаходженні невідомих сторін і кутів трикутника за відомими його сторонами та кутами. Результати в таких задачах наближені, тому що для більшості значень кутів наближеними є значення їх синуса і косинуса. Задача 1. Розв’язати трикутник за стороною й двома прилеглими кутами. На рисунку в трикутнику дано: a; […]...
- Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...
- Теорема Фалеса Геометрія Чотирикутники Теорема Фалеса Теорема 1 (Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні. На рисунку ; ; . Зверніть увагу: . Теорема має місце не тільки для сторін кута, а й для довільних прямих. Теорема 2 (про […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...
- Теорема про триперпендикуляри Геометрія Стереометрія Теорема про триперпендикуляри Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. Приклади застосування теореми про три перпендикуляри 1. На рисунку – куб. , тому […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
- Нерівність трикутника Геометрія Трикутники Нерівність трикутника Теорема. Які б не були три точки, відстань між будь-якими двома із цих точок не більша, ніж сума відстаней від них до третьої точки. Звідси випливає, що у будь-якому трикутнику кожна сторона менша за суму двох інших сторін, але більша за модуль різниці двох інших сторін. Якщо a, b і c […]...
- Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, якщо: – дві його висоти […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...