Головна ⇒ 📌Довідник з математики ⇒ Теорема Вієта

Теорема Вієта

Математика – Алгебра

Квадратні корені

Теорема Вієта

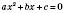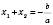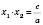Теорема 1 (Вієта). Якщо незведене квадратне рівняння Теорема Вієта має два корені, то Теорема Вієта, Теорема Вієта.
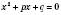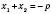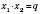Якщо зведене квадратне рівняння Теорема Вієта має два корені, то Теорема Вієта; Теорема Вієта.
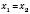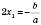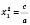
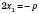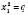Коли рівняння має один корінь, його можна вважати за два рівних: Теорема Вієта. Тоді для незведеного квадратного рівняння Теорема Вієта; Теорема Вієта

class=""/>; для зведеного Теорема Вієта, Теорема Вієта.
Зверніть увагу: для того щоб скористатися формулами теореми Вієта, треба спочатку переконатися у наявності коренів рівняння, перевіривши знак його дискримінанта.
Приклади
Знайти суму й додаток коренів рівняння.
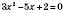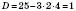1) Теорема Вієта;
Теорема Вієта – додатне число, і це означає, що рівняння має два корені.
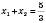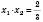Отже, Теорема Вієта; Теорема Вієта.
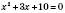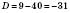2) Теорема Вієта;
Теорема Вієта – від’ємне число.
Рівняння
не має коренів, знайти їх суму та добуток неможливо.
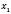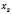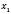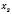Теорема 2 (обернена до теореми Вієта для зведених квадратних рівнянь). Якщо сума й добуток чисел Теорема Вієта і Теорема Вієта дорівнюють відповідно p і q, то Теорема Вієта і Теорема Вієта є коренями рівняння Теорема Вієта.
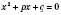Із теореми Вієта випливає, що цілі розв’язки рівняння 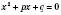Теорема Вієта є дільниками числа q. Користуючись оберненою теоремою, можна перевірити, чи є та чи інша пара дільників q коренями даного рівняння. Це дає можливість усно розв’язувати значну кількість зведених квадратних рівнянь.
Під час розв’язування треба також враховувати такі Висновки з теореми Вієта.
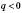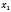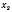1. Якщо Теорема Вієта, Теорема Вієта і Теорема Вієта мають різні знаки.
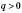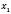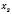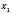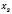2. Якщо Теорема Вієта, Теорема Вієта і Теорема Вієта обидва від’ємні чи обидва додатні. Знак Теорема Вієта і Теорема Вієта є протилежним до знака p.
Приклад
Теорема Вієта.
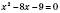За теоремою Вієта:
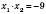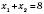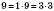Теорема Вієта; Теорема Вієта; Теорема Вієта.
Очевидно, що Теорема Вієта.
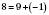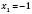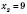Відповідь: Теорема Вієта; Теорема Вієта.




Related posts:

  1. Теорема Вієта Урок № 53 Тема. Теорема Вієта Мета: закріпити знання учнів щодо змісту теореми Вієта для зведеного квадратного рівняння та для квадратного рівняння загального виду; вдосконалити вміння відтворювати вивчені твердження, використовувати їх для розв’язування завдань, передбачених програмою з математики. Тип уроку: застосування знань та вмінь. Наочність та обладнання: опорний конспект “Теорема Вієта”. Хід уроку I. Організаційний […]...
  2. Теорема Вієта – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Теорема Вієта Щоб числа x1 та х2 були розв’язками рівняння ах2 + bх + с = 0, необхідно й достатньо, щоб:...
  3. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 55 Тема. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: перевірити рівень засвоєння учнями змісту основних понять теми “Квадратні рівняння” та рівень умінь, сформованих у ході вивчення теми. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити із виконаною […]...
  4. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 54 Тема. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: повторити, систематизувати та узагальнити знання і вміння учнів щодо виділення квадратних рівнянь серед інших рівнянь з однією змінною, класифікації квадратних рівнянь, а також застосування різних (передбачених програмою з математики) способів розв’язання квадратних рівнянь різного виду. Тип уроку: систематизація […]...
  5. Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...
  6. Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
  7. Теорема косинусів УРОК № 4 Тема. Теорема косинусів Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її. Хід уроку I. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань […]...
  8. Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
  9. Рівняння Математика – Алгебра Натуральні числа і дії над ними Рівняння Рівність, що містить невідоме число, називається Рівнянням. Значення невідомого, при якому рівняння перетворюється у правильну числову рівність, називається Розв’язком, або Коренем рів­няння. Розв’язати рівняння означає знайти всі його корені або довести, що їх немає. Кількість коренів рівняння Рівняння може: 1) не мати коренів: ; 2) […]...
  10. Формула коренів квадратного рівняння Математика – Алгебра Квадратні корені Формула коренів квадратного рівняння Корені квадратного рівняння знаходять за формулою . Вираз називається Дискримінантом і позначається буквою D. Кількість коренів 1. Якщо , рівняння не має коренів. 2. Якщо , рівняння має один корінь: . 3. Якщо , рівняння має два корені: . Для квадратних рівнянь із парним другим коефіцієнтом […]...
  11. Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
  12. Теорема Піфагора Урок № 34 Тема. Теорема Піфагора Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв’язування задач на знаходження невідомих сторін прямокутних трикутників. Типу уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання […]...
  13. Теорема про триперпендикуляри Геометрія Стереометрія Теорема про триперпендикуляри Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. Приклади застосування теореми про три перпендикуляри 1. На рисунку – куб. , тому […]...
  14. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Урок 8 Тема. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Мета уроку: вивчення теореми про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Які прямі в просторі називаються паралельними? 2) Вкажіть […]...
  15. Рівняння. Властивості рівносильності рівнянь Розв’яжіть задачі. 988. 1) 5х + 25 = 0; 5х = -25; х = -5; 2) 6у – 8 = 8; 6у = 16; у = 16/6; у= 3) 0,4x = 1,6; x = 1,6 : 0,4; x = 4; 4) 4у – 12 = 4; 4у = 16; y = 4. 989. 1) -2x […]...
  16. Теорема синусів УРОК № 7 Тема. Теорема синусів Мета уроку: вивчення теореми синусів. Формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: формулюють теорему синусів та доводять її. Хід уроку І. Перевірка домашнього завдання Перевірити правильність виконання домашніх […]...
  17. Теорема Фалеса Геометрія Чотирикутники Теорема Фалеса Теорема 1 (Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні. На рисунку ; ; . Зверніть увагу: . Теорема має місце не тільки для сторін кута, а й для довільних прямих. Теорема 2 (про […]...
  18. Теорема Фалеса Урок № 16 Тема. Теорема Фалеса Мета: формувати в учнів усвідомлене розуміння змісту теореми Фалеса та способу її доведення; формувати вміння відтворювати формулювання теореми Фалеса; застосовувати її для розв’язування задач на знаходження довжин відрізків, що відтинаються на сторонах паралельними прямими; розв’язувати задачі на поділ відрізка на п рівні відрізки або в даному відношенні. Тип уроку: […]...
  19. Види неповних квадратних рівнянь і їх розв’язання Математика – Алгебра Квадратні корені Види неповних квадратних рівнянь і їх розв’язання 1. Якщо , , квадратне рівняння набуває вигляду і має один корінь . 2. Якщо , , квадратне рівняння набуває вигляду . Розв’язуючи ­його, маємо: ; або . Рівняння має два корені: і . 3. Якщо , , квадратне рівняння набуває вигляду . […]...
  20. Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...
  21. Теорема, обернена до теореми Піфагора Урок № 35 Тема. Теорема, обернена до теореми Піфагора Мета: домогтися свідомого розуміння учнями змісту теореми Піфагора та її доведення: сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Формувати вміння відтворювати зміст вивченої теореми та застосовувати її під час розв’язування задач на доведення. Тип уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. […]...
  22. Узагальнена теорема Фалеса Урок № 25 Тема. Узагальнена теорема Фалеса Мета: сформувати в учнів поняття про відношення відрізків, пропорційні відрізки; сформувати свідоме розуміння учнями змісту теореми про пропорційні відрізки (узагальнення теореми Фалеса) та ідеї її доведення, а також можливість запису теореми у вигляді двох різних рівностей. Формувати в учнів уміння: – відтворювати зміст вивчених на уроці тверджень; – […]...
  23. ТЕОРЕМА ГАУЗЕ Екологія – охорона природи ТЕОРЕМА ГАУЗЕ – твердження, за яким два види не можуть співіснувати в одній і тій самій місцевості, якщо їхні екол. вимоги ідентичні, тобто вони займають одну й ту саму екол. нішу (див. також Принцип виключення Г. Ф. Гаузе). Це положення останнім часом дискусійне....
  24. Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...
  25. Розкладання многочлена на многочлени. Винесення спільного множника за дужки 437. 1) Якщо х = 4,32, то 6,32х – х2 = х(6,32 – х) = 4,32 • (6,32 – 4,32) = 4,32 • 2 = 8,64. 2) Якщо а = 1,5, b = -2,5, то а3 + а2b = а2(а + b) = 1,52 • (1,5 – 2,5) = 2,25 • (-1) = -2,25. 3) […]...
  26. Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...
  27. Лінійні рівняння та їх системи 831. 3) 7х – 2 = 10; 1), 2), 4) – не є рівняннями. 832. 1) 2х = 6; х = 3 – корінь рівняння; 4) 27 : х = 9; х = 3 – корінь рівняння. 833. 1) х + 7 = 9; х = 2 – розв’язок; 3) х – 8 = -6; […]...
  28. Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
  29. Вектор електричної індукції. Теорема Остроградського-Гаусса ФІЗИКА Частина 3 ЕЛЕКТРИКА І МАГНЕТИЗМ Розділ 8 ЕЛЕКТРИКА 8.5. Вектор електричної індукції. Теорема Остроградського-Гаусса Припустімо, що точковий заряд q міститься в центрі сферичного повітряного пухирця, який перебуває в певному середовищі, наприклад у маслі, діелектрична проникність якого ε=2. Напруженість електричного поля поблизу межі поділу повітря – масло на відстані r від заряду, меншій за радіус […]...
  30. Система двох лінійних рівнянь із двома невідомими – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Система двох лінійних рівнянь із двома невідомими – сталі. Правило Крамера: Квадратний тричлен – тричлен виду у = ах2 + bх + с, де х – змінна, а, b, с – константи і а ≠ 0. Одночлен ах2 називають старшим членом квадратного тричлена, а коефіцієнт а – старшим коефіцієнтом. Квадратний […]...
Ви зараз читаєте: Теорема Вієта
«
»