Теореми про ознаки паралелограма
Урок № 6
Тема. Теореми про ознаки паралелограма
Мета: сформувати в учнів свідоме розуміння змісту та схеми доведення теореми, що виражає ознаки паралелограма.
Формувати вміння:
– відтворювати ознаки та їхні доведення;
– застосовувати вивчені ознаки для доведення того, що даний чотирикутник є паралелограмом.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Паралелограм”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Домашнє завдання перевіряємо за
III. Формулювання мети й завдань уроку
З метою створення мотивації навчальної діяльності учнів та усвідомлення ними логіки побудови вивчення геометричних фігур (означення > властивості > ознаки) підводимо учнів до розуміння необхідності вміти знаходити серед чотирикутників паралелограми. Постає питання: чи існує відповідна ознака? Якщо так, її треба сформулювати та довести – це і є основна дидактична мета уроку.
IV. Актуалізація опорних знань
З метою свідомого розуміння та подальшого засвоєння учнями змісту ознак паралелограма сліз, активізувати знання і вміння учнів щодо
Для цього учні мають розв’язати вправи.
Виконання усних вправ за готовими рисунками
1 |
| Дано: АО = OD, BO = OC. Довести: AB = DC |
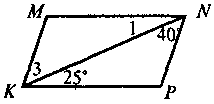
2 |
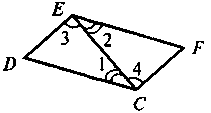
| Дано: Довести: |
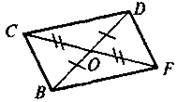
3 |
| Дано: BO = OD, CO = ОF. Довести: BF = CD |
4 |
| Знайти кути паралелограма |
V. Засвоєння знань
План вивчення нового матеріалу
1. Зміст поняття “ознака” паралелограма.
2. Теорема ознаки паралелограма: формулювання і доведення.
3. Приклади застосування ознак паралелограма.
@ На відміну від традиційного підручника геометрії (під ред. О. В. Погорєлова), в якому ознаки паралелограма розглядаються у формі опорних задач, та від інших під ручників (в яких ознаки були розглянуті як окремі теореми), новий підручник містить усі основні ознаки паралелограма (за двома протилежними сторонами, за парами протилежних сторін та за діагоналями) у вигляді однієї теореми. Такий підхід до викладання матеріалу мас логічне обгрунтування, оскільки всі ознаки паралелограма мають однакому схему доведення:
– спочатку доводиться рівність трикутників (здобутих у результаті проведення однієї або двох діагоналей паралелограма);
– із рівності трикутників випливає рівність відповідних елементів цих трикутників (які у свою чергу є елементами паралелограма);
– на основі доведеної рівності певних елементів паралелограма із використанням означення (а потім доведеного попереднього твердження) доводиться той факт, що даний чотирикутник – паралелограм.
Оскільки схеми доведення всіх трьох ознак майже однакові (відмінність тільки в застосуванні різних ознак рівності трикутників та використанні або означення паралелограма, або вже доведеної ознаки паралелограма за двома протилежними сторонами), то роботу з доведення ознак можна організувати так: ознаку паралелограма за двома протилежними сторонами доводить учитель за участі учнів, складає план доведення, а потім пропонує учням самостійно довести наступні ознаки за складеним планом.
Усі вивчені на уроці ознаки паралелограма поміщені в конспект “Паралелограм”.
VI. Формування первинних умінь та навичок
Виконання усних вправ
1. Діагоналі чотирикутника DEFK перетинаються в точці О, причому DO = OF, EO = OK. Назвіть паралельні сторони чотирикутника і поясніть, чому вони паралельні.
2. У чотирикутнику KLMN KL || MN і KL = MN. Назвіть рівні кути чотирикутника і поясніть, чому вони рівні.
3. У чотирикутнику PRSQ PR =SQ, PQ=RS. Знайдіть суму кутів R і S.
4. У чотирикутнику ABCD AB = CD. Яке співвідношення між сторонами чотирикутника необхідно додати до умови задачі, щоб довести, що ABCD – паралелограм? Наведіть усі можливі варіанти відповіді.
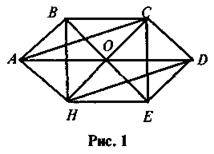
5. На рисунку 1 точка О – спільна середина відрізків AD, CH, BE. Які з чотирикутників є паралелограмами? Чому?
Виконання графічних вправ
Проведіть дві паралельні прямі. Відкладіть на одній із них відрізок AD, а на другій прямій – відрізок ВС, що дорівнює AD, так, щоб відрізки АВ і CD не перетиналися. Побудуйте відрізки АВ і CD.
А) Поясніть, чому чотирикутник ABCD є паралелограмом.
Б) Позначте точку М так, щоб чотирикутник АВМС був паралелограмом. Чи лежать точки М, С і D на одній прямій?
Виконання письмових вправ
1. Діагоналі чотирикутника ABCD перетинаються в точці О. Чи є даний чотирикутник паралелограмом, якщо АО = 4 см, ОС = 40 мм, BD = 1,2 дм, OD= 6 см? Відповідь бгрунтуйте.
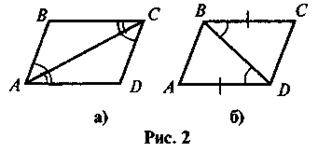
2. За даними рисунка 2 доведіть, що чотирикутник ABCD – паралелограм.
3. У чотирикутнику ABCD сторони АВ і CD паралельні. Знайдіть периметр чотирикутника, якщо АВ = CD = 9 см, АО = 4см.
Після засвоєння змісту теорем і формування первинних умінь застосовувати ознаки у стандартних ситуаціях розв’язуємо задачу з детальним поясненням.
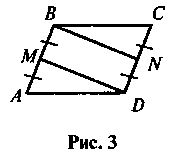
Задача. У паралелограмі ABCD точки М і N – середини сторін АВ і CD відповідно (рис. 3). Доведіть, що чотирикутник MBND – паралелограм.
Виконання письмових вправ
1. Діагоналі паралелограма ABCD перетинаються в точці О. Точки В1 і D1 – середини відрізків ВО і DO відповідно. Доведіть, що чотирикутник AB1CD1 – паралелограм.
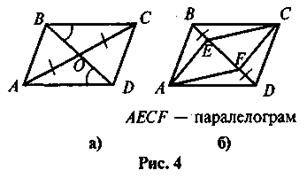
2. За даними рисунка 4 доведіть, що чотирикутник ABCD – паралелограм.
Під час розв’язування письмових вправ слід зробити акцент на тому, що ці задачі передбачають застосування властивостей паралелограма, але оскільки в умові цього не дано, то план розв’язування задач має бути таким:
– спочатку, використовуючи ознаки паралелограма, довести, що даний чотирикутник – паралелограм;
– після доведення того, що даний чотирикутник є паралелограмом, використати властивості паралелограма.
Зміна порядку виконання дій є логічною помилкою і суперечить логіці побудови геометрії.
VII. Підсумок уроку
Тестове завдання
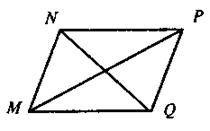
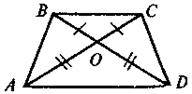
Діагоналі чотирикутника MNPQ (див. рис.) в точці перетину діляться навпіл. Одна з його сторін дорівнює 4 см. Чому дорівнює протилежна їй сторона?
1) 3 см; 2) 4 см; 3) 5 см; 4) 6 см.
VIII. Домашнє завдання
Вивчити формулювання і доведення теореми про ознаки паралелограма.
Розв’язати задачі.
1. Накресліть трикутник ABC і проведіть його медіану ВО. На промені ВО побудуйте відрізок OD, що дорівнює ВО. Сполучіть точку D з точками А і С.
А) Поясніть, чому чотирикутник ABCD є паралелограмом.
Б) Позначте точку М так, щоб чотирикутник ABDM був паралелограмом. Чи лежать точки М, С і D на одній прямій?
2. За даними рисунка 5 доведіть, що чотирикутник ABCD – паралелограм.
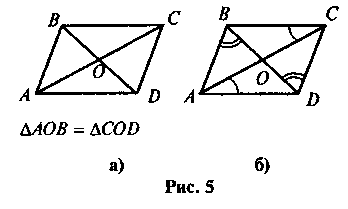
3. У чотирикутнику ABCD AB = CD, AD = BC. Знайдіть кути чотирикутника, якщо кут А втричі більший за кут В.
4. За даними рисунка 6 доведіть, що чотирикутник ABCD – паралелограм.
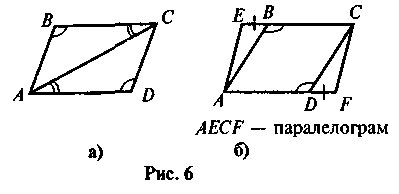
 1 =
1 =