Головна ⇒ 📌ГДЗ з математики ⇒ Тіла обертання

Тіла обертання

1008.

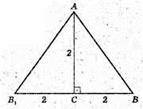
Осьовий переріз – це ΔARB1, де BB1 = 2 × СВ = 4 (см),

АС + В 1В, В 1C = СB.

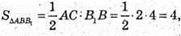S = 4 см2.

1009.

Sб. ц. = 2πrh = 2π × 2 × 10 = 40π (см2), Sб = 40π см2.

1010.

Sб. ц. = 4 × 5 = 20 (см2), Sб. ц. = 20 см2.

1011.

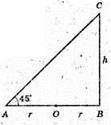
ΔАСВ: ∠B = 90°, ∠A = 45°. АВ = СВ. 2r = h,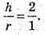

1012.

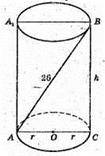
Дано циліндр. r = 5 м,

АА ВС – осьовий переріз. АВ = 26 см.

А) 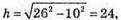h = 24 см;

Б) 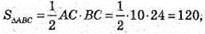SАА1BC =240 см2;

В) Sб.= 2πrh = 2π ×

5 × 24 = 240π, Sб. = 240π см2;

Г) Sп..ц. = 2πr(r + h) = 2π × 5 × 29 = 290π, Sп..ц. = 290π см2.

1013.

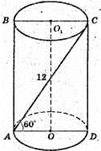
Циліндр.

Осьовий переріз ABCD, АС = 12 м.

CD + (ОСН).

А) H = ? CD = H,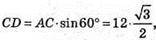

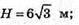
Б) r = ? 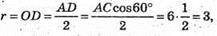r = 3м;

В)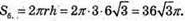

1014.

1015.

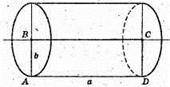
ABCD – прямокутник, AD = а,

АВ = b.

Sб. = 2πrh = 2π × b × а. r = b, h = а.

Г = a, h = Ь

Sб = 2πrh = 2π × а × b.

Площі бічних поверхонь циліндрів рівні.

1016.

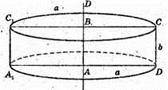
ABCD – осьовий

переріз. SABCD = S = 2r × h.

Sб. = 2πrh = S × π,

Sб. = S × π.

1017.

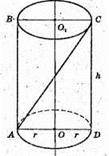
Циліндр, r, h, Діагональ осьового перерізу циліндра – це AC.

АС = h2 + 4r2 (рис. № 1016).

1018.

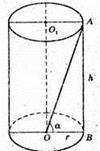
АВ = h, h = r tg α,

Sб. =2π × rh = 2πr × r tg α, Sб. = 2πr2 tg α.

1019.

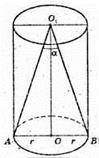
Циліндр.

AB = d,

∠AO1B = α. OO1 = H.

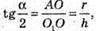
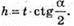
Sп. = 22πr2 + 2rh,

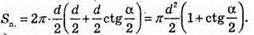
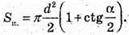
1021 .

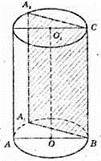
Площина AA1CD проходить через твірну CB циліндра,

Але не дотикається до циліндра.

Площини основ циліндра паралельні, тому в перерізі

A1C || A1B маємо паралельні прямі.

1022 .

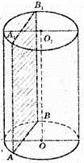
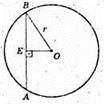
ОЕ + AB,

ОЕ = 6 см,

АЕ = BE.

ВО = r = 10 см.

ΔВОЕ: ∠E = 90°, ВО =10,

ЕО = 6.

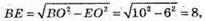
BE = 8 см. BA =16 см.

AA1B1B – прямокутник, AA1 = h = 16 см, AB = 16 см.

SAA1B1B = AB × AA 1 =16 × 16 = 256, S = 256 см 2.

1023.

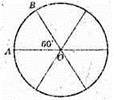
OA = OB = r. AB = r.

S перер. = r × h.

1024.

Sп. ц. = 50 см 2, S б. п. ц. = 30 см 2.

Sп. ц. = 2πrh + 2nr2 = 2nr(r + h).

2πrh = 30, 30 + 2πr2 =, 50, 2πr2 = 20, πr2 = 10,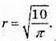

Sб. = 2πrh = 30,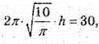

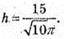
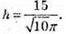
1025.

2πrh = Q, 2 2πr = h, h2 = Q,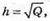

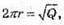
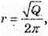
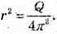
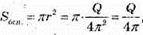
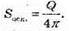
1026.

Top.

1027.

A = 4 см, r = 6 см.

S = πr2 + 2πrh = π(36 + 2 × 6 × 4) = π(36 + 48) = 84π = 253 см 2.

15 000 м2 = 1500 м2 = 13 500 м2 = 135 000 000 см2.

N = 135 000 000 : 253 = 533 500 (банок) = 533 600 банок.

1028.

D = 0,8 м, h = 3,8 м.

R = 40 смM, h = 380 см.

Sп = πr2 + 2πrh = π × 1600 + π × 80 × 380 = π x 32 000 см2.

Тиск дорівнює 10 × 32 000π = 320 000π

1030.

Ні. ·

(1 votes, average: 5.00 out of 5)

Тіла і поверхні обертання 905. На рисунку тіло, утворене обертанням прямокутника навколо його сторони. 906. А) Тіло, утворене обертанням прямокутного трикутника навколо катета, Б) Тіло, утворене обертанням прямокутного трикутника навколо гіпотенузи. ΔABC – прямокутний, AB – гіпотенуза. 907. Площина симетрії тіла обертання проходить через його вісь. 908. Див. рис. 909. У площині прямокутника ззовні його і паралельно одній з […]...

Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...

Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у паралельних […]...

Геометричні тіла і многокутники 868. ABCD – тетраедр, 6 ребер, 4 вершини, 4 грані. 869. Многогранник A1A2A3A4A5, 5 граней, 5 вершин, 8 ребер. 870. Многогранник, 5 граней, 6 вершин, 9 ребер. 872. 873. Див. рис. з № 872 S пов. тетр.=36 см2, S грані = 36 : 4 = 9, SABCD = 9 см2, а = ? 874. ABCDA1B1C1D […]...

Циліндр 940. Нехай дано циліндр, ABCD – осьовий переріз циліндра, AO = r – радіус циліндра, AC = d – діагональ осьового перерізу: А) ΔABC — прямокутний. BC – висота циліндра; Б) SABCD – площа діагонального перерізу. В) Площа бічної поверхні: Г) Площа поверхні циліндра 941. Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює D і […]...

Циліндр. Площа поверхні та об’єм циліндра УРОК № 56 Тема. Циліндр. Площа поверхні та об’єм циліндра Мета уроку: повторення, приведення в систему й розширення відомостей про циліндр, площу поверхні та об’єм циліндра; формування вмінь учнів знаходити площі поверхонь і об’єми циліндрів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі циліндрів. Вимоги до рівня підготовки учнів: пояснюють, що […]...

Комбінації геометричних фігур 1138. А2 =Q, 1139. D = 3а2, 1140. V = а3, 1141. ΔABD: ∠A = 90°, АВ = 6 см, AD =8 см. BD = 10 см. BB1DD – прямокутник, ∠B1DB =45° → ВВ1 = BD = 10 см. АA1 =ВВ1 =10 см. Vпарал. = 6 × 8 × 10 = 480 (см3)· 1142. Рис. […]...

Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...

Період і частота обертання тіла – Кінематика 5. Механіка 5.1. Кінематика 5.1.29. Період і частота обертання тіла Період обертання – це проміжок часу, за який тіло здійснює один повний оберт. Позначається буквою T. Одиниця вимірювання – одна секунда (1 с). Формула: Частота обертання – це кількість обертів тіла по колу за одиницю часу. Позначається буквою v (ню). Одиниця вимірювання – 1/с або […]...

Лабораторна робота № 4. ВИЗНАЧЕННЯ ПЕРІОДУ ОБЕРТАННЯ ТІЛА Тип уроку: урок формування практичних навичок. Мета: сформувати в учнів навички вимірювати період обертання тіла, обертову частоту та обчислювати швидкість руху тіла; виховувати в учнів охайність під час проведення експерименту, дбайливе ставлення до лабораторного обладнання; вчити учнів працювати в парах та групах. Обладнання та наочність: обладнання лабораторної роботи. Відеофрагмент: відеозапис фрагмента лабораторної роботи, за допомогою […]...

Лабораторна робота № 2 “Вимірювання частоти обертання тіла” РОЗДІЛ I МЕХАНІЧНИЙ РУХ УРОК № 8/8 Тема уроку. Лабораторна робота № 2 “Вимірювання частоти обертання тіла” Тип уроку: удосконалювання знань і вмінь. Мета уроку: формувати практичні навички вимірювання частоти обертання тіла; поглибити теоретичні знання учнів; розвивати навички самостійної роботи, творче мислення. План уроку Етапи Час Прийоми і методи I. Інструктаж з техніки безпеки 5 […]...

Умови рівноваги тіла, яке має вісь обертання. Важіль – Статика 5. Механіка 5.4. Статика 5.4.2. Умови рівноваги тіла, яке має вісь обертання. Важіль Важіль – це простий механізм для зрівноваження більшої сили меншою. Це тверде тіло (жорсткий стрижень), яке має вісь обертання. Якщо сили, які діють на важіль, розміщені по обидва боки від осі обертання або опори, то такий важіль називають важелем 1-го роду, якщо […]...

Момент сили. Умова рівноваги тіла, що має вісь обертання ЗАСТОСУВАННЯ ЗАКОНІВ ДИНАМІКИ Урок № 13 Тема. Момент сили. Умова рівноваги тіла, що має вісь обертання Мета: дати учням знання про момент сили і правило моментів: показати, що правило моментів виконується і для тіла, яке має незакріплену вісь обертання; пояснити значення правила моментів у побуті. Тип уроку: комбінований. План уроку Контроль знань 10 хв. 1. […]...

Рівномірний рух тіла по колу. Період і частота обертання. Кутова швидкість КІНЕМАТИКА Урок № 9 Тема. Рівномірний рух тіла по колу. Період і частота обертання. Кутова швидкість Мета: формувати знання про переміщення, шлях, швидкість і прискорення, про напрям миттєвої швидкості під час криволінійного руху, про період і частоту обертання тіла; порівняти переміщення, шлях, швидкість під час прямолінійного рівномірного, нерівномірного та криволінійного рухів; розповісти про широке застосування […]...

Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

Лабораторна робота № 1 “Визначення прискорення тіла в разі рівноприскореного руху” 1-й семестр МЕХАНІКА 1. Кінематика Урок 12/14 Тема. Лабораторна робота № 1 “Визначення прискорення тіла в разі рівноприскореного руху” Мета уроку: виміряти прискорення кульки, що скочується по похилому жолобу Тип уроку: контролю й оцінювання знань Обладнання: металевий жолоб, штатив з муфтою й затискачем, сталевий циліндр, вимірювальна стрічка, секундомір або годинник із секундною стрілкою ХІД РОБОТИ […]...

Геометричні тіла 628. А) спільна вершина; Б) спільне ребро; В) спільна грань; Г) спільна діагональ. 629. А) дві кулі не мають спільних точок; Б) дві кулі мають одну спільну точку; В) дві кулі, які перетинаються; Г) кулі мають різні радіуси і спільний центр. 630. Дано точку О і r > 0, г – відстань. ОХ ≤ r. […]...

Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...

Властивості циліндра 1. 1) В перерізі циліндра площиною трикутник отримати не можна. 2) Прямокутник може бути перерізом циліндра, який проходить через вісі циліндра, або їй паралельний. 3) Трапеція не може бути перерізом циліндра. 4) Квадрат може бути перерізом циліндра, який є рівностороннім. Відповідь: 1) ні; 2) так; 3) ні; 4) так для рівносторонього циліндра. 2. ГМТ, рівновіддалених […]...

Урок 2. Тіла. Характеристики тіла: довжина, маса, об’єм, густина. Їх вимірювання Урок 2. Тіла. Характеристики тіла: довжина, маса, об’єм, густина. Їх вимірювання Мета: формувати уявлення про реальні об’єкти, що оточують людину; формувати навички безпечного користування вимірювальними приладами (терези, мірний циліндр), вміння визначати масу, об’єм та розміри тіл; розвивати вміння організовувати свою роботу (самоорганізовуватися), виховувати спостережливість. Обладнання: лінійка, штангенциркуль, мірний циліндр, терези, ареометр, по три кульки з […]...

Геометричні тіла і поверхні 219. Дано: FABCD – піраміда правильна, AB = 6 см, ∠DFC = 60°. 1) Знайти SABCD i висоту FO. SABCD = 62 = 36 (см2). ΔDFC, DF = FC за умовою І ∠DFC = 60° → DF = FC = DC = 6 (см). Відповідь: 36 см2, 2) ∠FCA – ? Відповідь: 3) ∠AFC – […]...

Об’єм прямої призми і циліндра 1158. Нехай ABCA1B1C1 – призма, AB = BC = AC, AC1 = d, ∠C1AC = α. З ΔC1AC: C1C = AC 1 × sin α = d × sin α; AC = AC1 × cos α = d × cos α. Знайдемо Відповідь: 1159. Нехай AA1D1D – переріз заданої призми, SAA1D1D = 4 см2. KL […]...

Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...

Вписана та описана сфера 1. Нехай О А – радіус кулі, ОА = 1 см. АВ = ΚΚ1 = 2ОА = 2 см. CD = 2СО = 2 см. Sбіч. = PKLMN× КК1 = 4 × 2 × 2 = 16 (см2). Відповідь: 16 см2. 2. Нехай АВ =AD = ВВ1 = а. З ΔABD: З ΔΒ1BD: В1D2 = […]...

Обчислення об’ємів тіл за допомогою інтеграла 1210. Об’єм призми обчислимо за формулою: V = Sосн. × Н, де H – висота призми. V = Q × l × sin а. Відповідь: l sin а. 1211. Нехай ABCDA1B1CD1- паралелепіпед. AB = 6 дм, AD = 8 дм, ∠BAD = 45°, AA= 7 дм, ∠AAK = 45°. З ΔA1AK: Отже, об’єм V паралелепіпеда […]...

Інертність тіла. Маса тіла МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ § 23. Інертність тіла. Маса тіла Запитання до вивченого 1. Інертність – це властивість тіла, яка полягає в тому, що для зміни його швидкості під час взаємодії з будь-якими іншими тілами потрібен певний час. 2. Маса тіла – це фізична величина, яка характеризує інертність тіла. Чим більша маса тіла, тим […]...

Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...

Об’єми призми і циліндра 1. Радіус циліндричної цистерни відомий, а висоту рідини заміряємо за допомогою вертикального прута і знайдемо об’єм рідини за формулою об’єму циліндра. 2. Об’єм сараю V складається з об’єму паралелепіпеда ABCDA1B1C1D1 і об’єму призми A1ED1B1FC1 в основі якої лежить рівнобедрений прямокутний трикутник. 1 випадок AA1 = 6м, AD = 7,5м, CD = 12м. 3 ΔA1ED1: ∠A1ED1 […]...

Лабораторна робота № 10. З’ЯСУВАННЯ УМОВ ПЛАВАННЯ ТІЛА Тип уроку: урок формування практичних навичок. Мета: дослідним шляхом з’ясувати умови плавання тіл; виховувати в учнів охайність під час проведення експерименту, дбайливе ставлення до лабораторного обладнання; вчити учнів працювати в парах та групах. Обладнання та наочність: обладнання лабораторної роботи. Відеофрагмент: відеозапис фрагмента лабораторної роботи, за допомогою якого вчитель акцентує увагу на ході вимірювань, які виконують […]...

Лабораторна робота № 13 “Визначення питомої теплоємності речовини” 2-й семестр ТЕПЛОВІ ЯВИЩА 4. Кількість теплоти. Теплові машини Урок 10/52 Тема. Лабораторна робота № 13 “Визначення питомої теплоємності речовини” Мета уроку: навчитися визначати питому теплоємність речовини калориметричним способом. Тип уроку: урок контролю й оцінювання знань. Обладнання: склянка з водою, калориметр, термометр, ваги з набором гир, вимірювальний циліндр (мензурка), металевий циліндр на нитці, посудина (одна […]...

Об’єм конуса і зрізаного конуса 1295. Нехай SA – твірна конуса, ∠SAO = α, SA = l. З ΔSAO : SO = SA × sin ∠SAO = I sin α, AO = AS × cos ∠SAO = І × cos α. Отже, об’єм конуса V дорівнює: Відповідь: 1296. Нехай радіус основи свинцевого конуса дорівнює r, а висота циліндра – H. […]...

АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ № 2. ЯВИЩЕ ІНЕРЦІЇ. ІНЕРТНІСТЬ ТІЛА. МАСА ТІЛА Тип уроку: комбінований урок. Мета: надати учням уявлення про особливості взаємодії тіл, про інертність, про явище інерції, ввести поняття маси. Обладнання та наочність: досліди, що ілюструють явище інерції, портрет Галілея, Ньютона, фотографії еталону маси. Відеофрагмент: рух тіла по інерції. Хід уроку I. ОРГАНІЗАЦІЙНИЙ ЕТАП II. АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ _____________________________________________________ _____________________________________________________ _____________________________________________________ _____________________________________________________ III. АКТУАЛІЗАЦІЯ ОПОРНИХ […]...

РУХ ТІЛА, КИНУТОГО ПІД КУТОМ ДО ГОРИЗОНТУ – РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.3. РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) 2.3.2. РУХ ТІЛА, КИНУТОГО ПІД КУТОМ ДО ГОРИЗОНТУ Траєкторія руху тіла – парабола (рис. 39). Дальність польоту тіла, кинутого під кутом α до горизонту: Рис. 39 Максимальна висота піднімання тіла Час руху:...

РУХ ТІЛА, КИНУТОГО ГОРИЗОНТАЛЬНО – РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.3. РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) 2.3.1. РУХ ТІЛА, КИНУТОГО ГОРИЗОНТАЛЬНО Тіло, кинуте горизонтально, рухається по параболічній траєкторії: його рух складається із руху горизонтального зі сталою швидкістю 0 і вільного падіння з нульовою початковою швидкістю. На рис. 37 зображено рух тіла, […]...

Об’єм кулі та її частин 1338. А) Нехай ABCDA1В1C1D1 – куб. Оскільки куля вписана в куб з ребром а, то 2г = а, Отже, об’єм кулі Б) Оскільки діагональ куба дорівнює двом радіусам кулі, то знайдемо діагональ З ΔB1BD: Отже, радіус, кулі Об’єм кулі V дорівнює: Відповідь: а) б) 1339. Нехай SA – твірна конуса. ∠SAO = α. З ΔSAO: […]...

Конус і зрізаний конус 983. Нехай дано конус, твірна якого AM = l, і нахилена до площини основи під кутом ∠MAO = α. А) ΔAMO – прямокутний. OM – висота, OM = l × sin α; Б) AO – радіус основи конуса. AO = l × cos α; В) ΔAMB – осьовий переріз; Г) площа основи конуса – площа […]...

ВАГА ТІЛА. ВАГА ТІЛА, ЯКЕ РУХАЄТЬСЯ З ПРИСКОРЕННЯМ. ПЕРЕВАНТАЖЕННЯ. НЕВАГОМІСТЬ – СИЛИ В МЕХАНІЦІ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.2. СИЛИ В МЕХАНІЦІ 2.2.4. ВАГА ТІЛА. ВАГА ТІЛА, ЯКЕ РУХАЄТЬСЯ З ПРИСКОРЕННЯМ. ПЕРЕВАНТАЖЕННЯ. НЕВАГОМІСТЬ Вага тіла – це сила, з якою тіло діє на опору чи підвіс унаслідок притягання його до Землі. Якщо опора перебуває в спокої або рухається рівномірно і прямолінійно, то вага […]...

ІНЕРТНІСТЬ ТІЛА. МАСА ТІЛА Розділ 3 ВЗАЄМОДІЯ ТІЛ. СИЛА &23. ІНЕРТНІСТЬ ТІЛА. МАСА ТІЛА Спостереження 1. М’яч падає на поверхню Землі, а потім відскакує від неї – це приклад взаємодії двох тіл. Ми вже знаємо, що результатом взаємодії тіл є зміна їх швидкості і напряму руху. М’яч після зіткнення відскакує майже з такою самою швидкістю, але у зворотному напрямі, […]...

ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...

Обертання зір у Галактиці §15.Будова Всесвіту 3. Обертання зір у Галактиці Сонце розташоване поблизу площини Галактики на відстані 25000 св. років від її ядра. Вектор швидкості Сонця відносно найближчих зір спрямований до сузір’я Геркулес. Разом з усіма сусідніми зорями Сонце обертається навколо ядра Галактики зі швидкістю 250 км/с. Період обертання Сонця навколо ядра називається галактичним роком, який дорівнює 250000000 […]...

Ви зараз читаєте: Тіла обертання

« Зв’язок людини і природи. Pух середньовічного населення

Особливості навчання української мови у школах з російською мовою викладання »

Related posts: