Головна ⇒ 📌Математика ⇒ Трикутник і його види

Трикутник і його види

Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ

§ 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

14. Трикутник і його види

З усіх многокутників трикутники мають найменшу кількість сторін.

Трикутники можна розрізняти за видом їх кутів.

Якщо всі кути трикутника гострі, то його називають гострокутним трикутником (рис. 117).

Якщо один із кутів трикутника прямий, то його називають прямокутним трикутником (рис. 118).

Якщо один із кутів трикутника тупий, то його називають тупокутним трикутником (рис. 119).

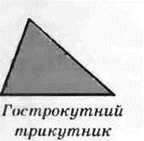
Рис.

117

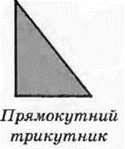
Рис. 118

Рис. 119

Говорять, що ми класифікували трикутники за видом їх кутів.

Трикутники можна класифікувати не тільки за видом кутів, а й за кількістю рівних сторін.

Якщо дві сторони трикутника рівні, то його називають рівнобедреним трикутником.

На рисунку 120 зображено рівнобедрений трикутник ABC, у якого АВ = ВС. На рисунку рівні сторони позначають однаковою кількістю штрихів. Рівні сторони АВ і ВС називають бічними сторонами, а сторону АС – основою рівнобедреного трикутника ABC.

Якщо три сторони трикутника рівні, то його називають

рівностороннім трикутником.

Трикутник, зображений на рисунку 121, – рівносторонній, у нього MN = NE = ЕМ.

Якщо три сторони трикутника мають різні довжини, то його називають різностороннім трикутником.

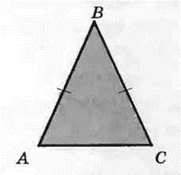
Рис. 120

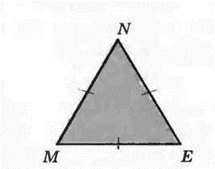
Рис. 121

Трикутники, зображені на рисунках 117-119, – різносторонні.

Якщо сторона рівностороннього трикутника дорівнює а, то його периметр Р обчислюють за формулою

Р = 3а

Приклад 1 За допомогою лінійки і транспортира побудуйте трикутник, дві сторони якого дорівнюють 3 см і 2 см, а кут між ними – 50°.

Розв’язання. За допомогою транспортира побудуємо кут А, градусна міра якого 50° (рис. 122). Па сторонах цього кута від його вершини за допомогою лінійки відкладемо відрізок АВ завдовжки 3 см і відрізок АС завдовжки 2 см (рис. 123). Сполучивши відрізком точки В і С, отримаємо шуканий трикутник ABC (рис. 124).

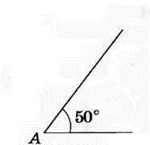
Рис. 122

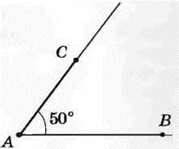
Рис. 123

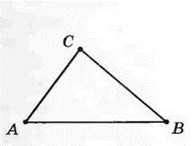
Рис. 124

ПРИКЛАД 2 За допомогою лінійки і транспортира побудуйте трикутник ABC, сторона АВ якого дорівнює 3 см, а кути САВ і СВА відповідно дорівнюють 40° і 110°.

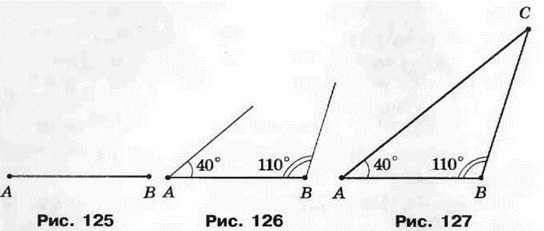
Розв’язання. За допомогою лінійки будуємо відрізок АВ завдовжки 3 см (рис. 125). Від променя АВ за допомогою транспортира відкладаємо кут з вершиною н точці А, градусна міра якого дорівнює 40°. Від променя ВА по той самий бік від прямої АВ, по який було відкладено перший кут, відкладаємо кут з вершиною в точці В, градусна міра якого дорівнює 110° (рис. 126). Знайшовши точку С перетину сторін кутів А і Б, отримаємо шуканий трикутник ABC (рис. 127).

Розв’язуємо усно

1. Чому дорівнює периметр восьмикутника, кожна сторона якого дорівнює 4 см?

2. Обчисліть суму 27 + 16 + 33 + 24.

3. Яких чисел не вистачає в ланцюжку обчислень?

4. На трьох кущах розквітло 15 троянд. Коли на одному з цих кущів розпустилися ще 3 троянди, то на всіх кущах троянд стало порівну. Скільки троянд було на кожному кущі спочатку?

Вправи

342.° Визначте вид трикутника, зображеного на рисунку 128, залежно від виду його кутів та кількості рівних сторін.

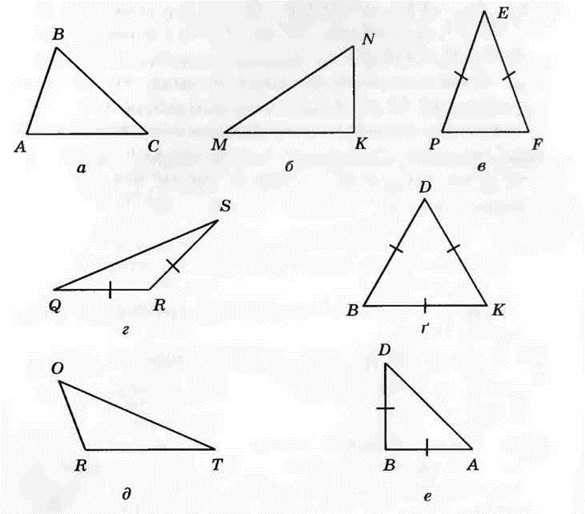
Рис. 128

343.° Нарисуйте:

1) різносторонній гострокутний трикутник;

2) рівнобедрений прямокутний трикутник;

3) рівнобедрений тупокутний трикутник.

344.° Нарисуйте:

1) різносторонній прямокутний трикутник;

2) різносторонній тупокутний трикутник;

3) рівнобедрений гострокутний трикутник.

345.° Знайдіть периметр трикутника із сторонами 16 см, 22 см і 28 см.

346.° Знайдіть периметр трикутника із сторонами 14 см, 17 см і 17 см.

347.° Нарисуйте довільний трикутник, виміряйте його сторони та кути, обчисліть периметр і суму кутів цього трикутника.

348.° Одна сторона трикутника дорівнює 24 см, друга сторона на 18 см більша за першу, а третя у 2 рази менша від другої. Знайдіть периметр трикутника.

Одна сторона трикутника дорівнює 12 см, друга сторона у 3 рази більша за першу, а третя на 8 см менша від другої. Знайдіть периметр трикутника.

350.° 1) Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює 13 см, а бічна сторона – 8 см.

2) Периметр рівнобедреного трикутника дорівнює 39 см, а основа – 15 см. Знайдіть бічні сторони трикутника.

351.° Периметр рівнобедреного трикутника дорівнює 28 см, а бічна сторона – 10 см. Знайдіть основу трикутника.

352.° Периметр трикутника дорівнює р см, одна сторона – 22 см, друга сторона – b см. Складіть вираз для знаходження третьої сторони. Обчисліть довжину третьої сторони, якщо р = 72, b = 26.

353.° Периметр трикутника дорівнює 97 см, одна сторона – а см, друга сторона – b см. Складіть вираз для знаходження третьої сторони. Обчисліть довжину третьої сторони, якщо а = 32, b = 26.

354.° За допомогою лінійки і транспортира побудуйте трикутник та вкажіть його вид, якщо:

1) дві сторони дорівнюють 3 см і 6 см, а кут між ними – 40°;

2) дві сторони дорівнюють 2 см 5 мм і 5 см, а кут між ними – 130°;

3) дві сторони дорівнюють по 3 см 5 мм, а кут між ними – 54°;

4) одна сторона дорівнює 4 см, а кути, що прилягають до цієї сторони, – 30° і 70°;

5) одна сторона дорівнює 2 см 5 мм, а кути, що прилягають до цієї сторони, – 100° і 20°;

6) одна сторона дорівнює 5 см, а кути, що прилягають до цієї сторони, – 30° і 60°;

7) одна сторона дорівнює 5 см 5 мм, а кути, що прилягають до цієї сторони, – по 45°;

8) одна сторона дорівнює 5 см 5 мм, а кути, що прилягають до цієї сторони, – по 60°.

355.° За допомогою лінійки і транспортира побудуйте трикутник та вкажіть його вид, якщо:

1) дві сторони дорівнюють 3 см і 4 см, а кут між ними – 90°;

2) дві сторони дорівнюють по 4 см 5 мм, а кут між ними – 60°;

3) одна сторона дорівнює 6 см, а кути, що прилягають до цієї сторони, – 90° і 45°;

4) одна сторона дорівнює 4 см 5 мм, а кути, що прилягають до цієї сторони, – по 35°.

356.°° Побудуйте трикутник, сторони якого містять чотири точки, зображені на рисунку 129.

Рис. 129

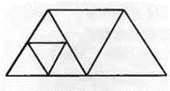
Рис. 130

Рис. 131

357.° Скільки трикутників зображено на рисунку 130?

358.° Скільки трикутників зображено на рисунку 131?

Вправи для повторення

359. Запишіть усі кути, зображені на рисунку 132, і вкажіть вид кожного кута.

360. Михайлик виконував домашнє завдання з математики з 16 год 48 хв до 17 год 16 хв, а Дмитрик – із 17 год 53 хв до 18 год 20 хв. Хто з хлопчиків довше виконував завдання та на скільки хвилин?

361. Розв’яжіть рівняння:

1) 429 + m = 2106; 3) (m + 326) – 569 = 674;

2) 348 – k = 154; 4) 5084 – (k – 299) = 568.

362. Замість зірочок поставте цифри так, щоб дія була виконана правильно:

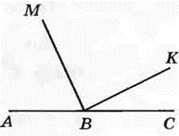
Рис. 132

Задача від Мудрої Сови

363. Кожен учень гімназії вивчає принаймні одну з двох іноземних мов. Англійську мову вивчають 328 учнів, французьку мову – 246 учнів, а англійську та французьку одночасно – 109 учнів. Скільки всього учнів навчається в гімназії?