Величина кута. Вимірювання і побудова кутів
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 20.Величина кута. Вимірювання і побудова кутів
Кути, як і відрізки, можна вимірювати.
Поділимо прямий кут на 90 рівних частин (рис. 100). Міру однієї такої частини беруть за одиницю вимірювання кутів і називають градусом1. Позначають так: 1°. Градусна міра прямого кута дорівнює 90°, а розгорнутого – І80° (рис. 101). Можна сказати інакше: прямий кут дорівнює 90°, а розгорнутий – 180°. Градусну міру кута позначають так само, як і кут. Наприклад, на рисунку 102 градусна міра кута

Рис. 100
1 Від латинського слова gradus – крок, ступінь.
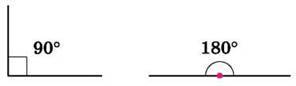
Рис. 101
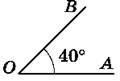
Рис. 102
Кути в градусах вимірюють за допомогою приладу, який називається транспортиром (рис. 103). Шкала транспортира розміщена на півколі і має 180 поділок. Кожна поділка шкали дорівнює 1°. Центр транспортира позначено точкою O.

Рис. 103
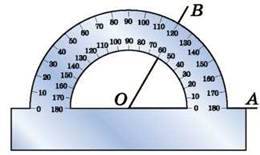
Рис. 104
Рис. 105
Щоб виміряти кут, потрібно накласти на нього транспортир так, як показано на рисунках 104 та 105: центр транспортира має збігатися з вершиною нює сумі кутів АОВ і ВОС, ∠АОС = ∠AOB + ∠ВОС. Оскільки ∠AОВ = 30°, ∠ВОС = 50°, то ∠AOC = 30° + + 50° = 80°.
Якщо ∠MON = 110°, ∠KON = 40° (рис. 109), то щоб знайти градусну міру кута МОК, потрібно
∠МОK = ∠MON – ∠KON = 110° – 40° = 70°.
Промінь ОK ділить кут АОВ на два рівні кути (рис. 110). Такий промінь називається бісектрисою кута.
Отже,
Промінь, якии виходить з вершини кута і розбиває його на два рівні кути, називається бісектрисою кута.
Приклад. ОK – бісектриса кута АОВ. ∠AОK = = 37°. Знайди ∠AОВ.
Розв’язання. ∠AОВ = ∠AОK ∙ 2 = 37° ∙ 2 = 74°.
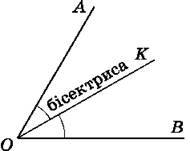
Рис. 110
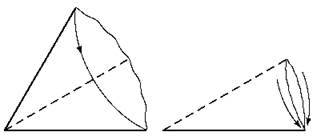
Рис. 111
Якщо взяти кут, вирізаний з аркуша паперу, то його бісектрису легко знайти за допомогою перегинання. Кут треба скласти так, щоб його сторони збіглися. Тоді лінія перегину і буде бісектрисою цього кута (рис. 111).
Початковий рівень
667. Які з тверджень правильні, а які – хибні:
1) кут, який дорівнює 50°, гострий;
2) кут, який дорівнює 86°, тупий;
3) кут, який дорівнює 92°, прямий;
4) кут, який дорівнює 115°, тупий;
5) кут, який дорівнює 91°, гострий;
6) кут, який дорівнює 180°, розгорнутий.
668. Які з даних кутів гострі, тупі, прямі або розгорнуті:
1) ∠А = 17°; 2) ∠B = 117°; 3) ∠С = 90°;
4) ∠D = 1°; 5) ∠Е = 180°; 6) ∠F = 179°;
7) ∠G = 89°; 8) ∠Н = 94°?
669. Які з даних кутів гострі, тупі, прямі або розгорнуті:
1) ∠М = 42°; 2) ∠N = 90°; 3) ∠О = 113°;
4) ∠Р = 7°; 5) ∠R = 97°; 6) ∠S = 81°;
7) АТ = 180°; 8) ∠Q = 178°?
670. Визнач (усно) за рисунком 112 градусні міри кутів:
1) AOK, AOL, АОМ, AON;
2) BON, BOM, BOL, ВОК.
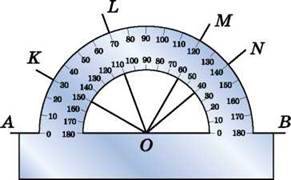
Рис. 112
671. (Усно). Відомо, що ∠АОР = ∠РОВ (рис. 113 і рис. 114). Чи є промінь ОР бісектрисою кута АОВ? Відповідь поясни.
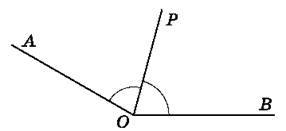
Рис. 113
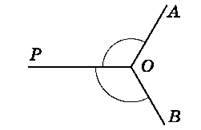
Рис. 114
672. На яких рисунках 115-117 промінь OP є бісектрисою кута AOB?
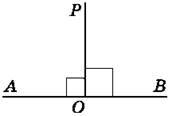
Рис. 115
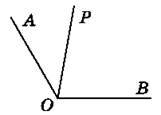
Рис. 116
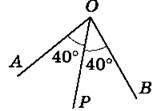
Рис. 117
Середній рівень
673. За допомогою транспортира виміряй кути, зображені на рисунку 118, і запиши результати вимірювань у зошит.
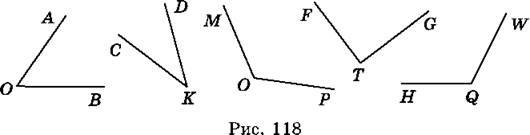
674. За допомогою транспортира виміряй кути, зображені на рисунку 119. Запиши результати вимірювань у зошит.
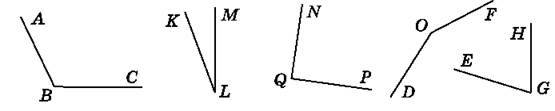
Рис. 119
675. Виміряй транспортиром кути KON, NOM, КОМ (рис. 120). Обчисли суму кутів KON і NOM. Зроби висновок.
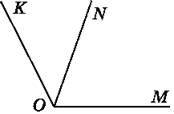
Рис. 120
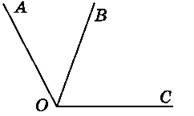
Рис. 121
676. Виміряй кути AOB, BOC, AOC на рисунку 121. Обчисли різницю ∠AOC – ∠AOB. Зроби висновки.
677. Накресли в зошиті гострий і тупий кути. Виміряй їх за допомогою транспортира.
678. Накресли кут, який дорівнює 25°, 45°, 80°, 105°, 135°, 145°.
679. Накресли кут, який дорівнює 30°, 55°, 70°, 110°, 130°, 155°.
680. На рисунку 122 ∠PNK = 62°. Обчисли градусну міру кута MNP.
681. За даними рисунка 123 знайди градусну міру кута DOC.
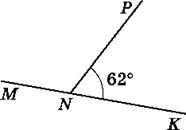
Рис. 122
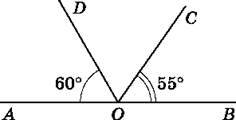
Рис. 123
682. Знайди градусну міру кута AOB на рисунку 124 і рисунку 125.
683. На рисунку 126 ∠АОС = 90°, ∠ВОС = 30°. Обчисли градусну міру кута АОВ.
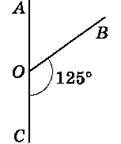
Рис. 124
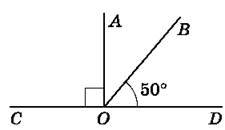
Рис. 125
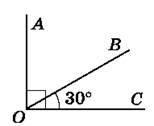
Рис. 126
684. Промінь OK ділить кут АОВ на два кути: АОК і КОВ. Знайди градусну міру кута АОВ, якщо ∠AOK = = 52°, ∠KOB = 43°.
685. Промінь ON ділить кут AOB на два кути: AON і NOB. Знайди градусну міру кута AOB, якщо ∠ AON = 37°, ∠NOB = 59°.
686. За допомогою транспортира побудуй бісектрису кута, що дорівнює:
1) 70°; 2) 90°; 3) 140°.
687. За допомогою транспортира побудуй бісектрису кута, що дорівнює:
1) 50°; 2) 84°; 3) 130°.
688. Побудуй на аркуші паперу тупий кут. Побудуй “на око” бісектрису цього кута. Перевір побудову перегинанням аркуша.
689. Побудуй на аркуші паперу гострий кут. Побудуй “на око” бісектрису цього кута. Перевір побудову перегинанням аркуша.
690. Знайди кут між бісектрисою і стороною даного кута, що дорівнює:
1) 16°; 2) 38°; 3) 102°.
Достатній рівень
691. Знайди градусну міру кута між стрілками годинника, якщо він показує:
1) 1 год; 2) 2 год; 3) 3 год;
4) 5 год; 5) 8 год; 6) 10 год.
Розв’язання. 1) О 6 год стрілки утворюють кут
180°. Оскільки на шкалі між числами 12 і 6 є 6 поділок, то о 1 год стрілки утворюють кут 180° : (12 – 6) = = 30°.
692. Накресли кут AOB, який дорівнює 120°. Потім накресли промінь ОС так, щоб ∠AOC дорівнював 30° (два способи). Виміряй ∠BOC, що утворився.
693. 1) У яку ціль влучить кулька (рис. 127), якщо удар по ній від точки відліку (0°) спрямовано: а) на 90°; б) на 150°; в) на 30°?
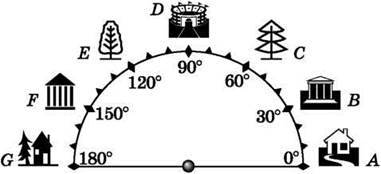
Рис. 127
2) Скільки градусів між цілями: а) деревом і ялинкою; б) ялинкою і будинком А; в) ялинкою і будинком G; г) будинком А і будинком F?
694. Виміряй кут АОС (рис. 128) та обчисли кути КОС і СОМ.
695. Виміряй транспортиром кут NOK (рис. 129) та обчисли кути MOK та LOK.
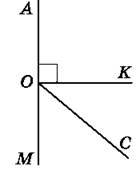
Рис. 128
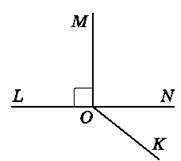
Рис. 129
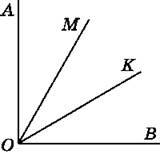
Рис. 130
696. Прямий кут АОВ поділено променями ОМ і ОК так, що ∠AOK = 63°, а ∠BOM = 56° (рис. 130). Обчисли градусну міру кута МОК.
697. Розгорнутий кут COD поділено променями ON і OK так, що ∠DON = 130°, ∠COK = 110° (рис. 131). Знайди градусну міру кута NOK.
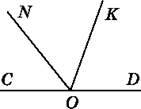
Рис. 131
698. Знайди градусну міру кута та визнач його вид, якщо бісектриса кута утворює з однією із його сторін:
1) 17°; 2) 45°; 3) 79°.
699. Накресли кут АОВ, градусна міра якого 60°. За допомогою транспортира проведи промінь OC так, щоб промінь OA був бісектрисою кута ВОС.
700. На рисунку 132 МС – бісектриса ∠AMD і MB – бісектриса ∠AMC. Знайди градусну міру кута AMD, якщо ∠BMC = 35°.
701. На рисунку 132 MC – бісектриса ∠AMD і MB – бісектриса ∠AMC. Знайди градусну міру кута AMB, якщо ∠AMD = 136°.
702. Накресли розгорнутий кут ABC, поділи його променем BK на два кути. Побудуй промінь BD – бісектрису ∠ABK і промінь BM – бісектрису∠KBC. Виміряй градусну міру кута DBM. Зроби висновки.
Високий рівень
703. На рисунку 133 РК – бісектриса ∠APC; ∠APB – розгорнутий кут. ∠KPB = 124°. Знайди градусну міру кута АРС.
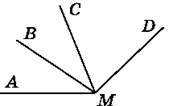
Рис. 132
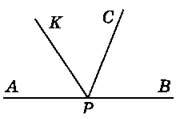
Рис. 133
704. На рисунку 133 PK – бісектриса ∠APC, ∠APB – розгорнутий кут. ∠APC = 118°. Знайди градусну міру кута KPB.
705. Кут МОК у три рази менший від кута KON (рис. 134). Знайди ці кути, якщо ∠MON = 140°.
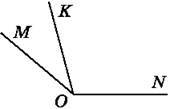
Рис. 134
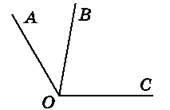
Рис. 135
706. Кут AOB у два рази менший від кута BOC (рис. 135). Знайди ці кути, якщо ∠AOC = 120°.
707. Накресли пряму АВ і познач на ній точку О. Потім побудуй кут АОС, який дорівнює 120°, і кут BOD, який дорівнює 35° (двома способами). Обчисли ∠COB і ∠COD.
708. З вершини прямого кута проведено промінь так, що він ділить прямий кут на два кути, градусна міра одного з яких на 10° більша за міру іншого. Знайди градусну міру кожного з утворених кутів.
709. На рисунку 136 QB – бісектриса ∠AQC; QD – бісектриса ∠CQE. Знайди кут AQE, якщо ∠DQB = 68°.
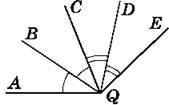
Рис. 136
Вправи для повторення
710. Не розв’язуючи рівняння, знайди, яке із чисел 5, 6, 7, 8 є коренем рівняння:
1) 5(x – 2) + 4 = 24; 2) 12 – 3(x – 5) = 6;
3) 12 + 3(x + 7) = 57; 4) 9 (x + 3) – 12 = 60.
711. Як зміниться сума чисел 2317 і 5372, якщо до першого числа додати 712, а до другого – 611?
712. Заповни ланцюг розрахунків:
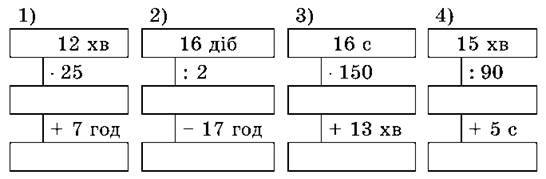
713. Понови запис: