Головна ⇒ 📌Довідник з математики ⇒ Відношення та пропорції
Відношення та пропорції
Математика – Алгебра
Множення і ділення звичайних дробів
Відношення та пропорції
Відношенням двох чисел називається частка цих чисел. Відношення показує, у скільки разів одне число більше від другого або яку частину становить одне число від другого.
Щоб знайти відношення двох величин, вони мають бути виміряні однією й тією ж одиницею вимірювання. Наприклад, відношення 3 км до 50 см дорівнює 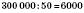 , тому що 3 км == 300000 см.
, тому що 3 км == 300000 см.
Рівність двох відношень називається Пропорцією.
Приклади
1) 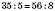
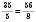 .
.2)
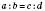 , або
, або 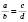 .
.Читають: а так відноситься до b, як c до d. У наведеному записі числа a і d називають крайніми членами пропорції, а числа b і c – середніми членами. Вважаємо, що a, b, c, d не дорівнюють 0.
Основна властивість пропорції
В істинній пропорції добуток крайніх членів дорівнює добутку середніх, і навпаки: якщо добуток крайніх членів пропорції дорівнює добутку середніх членів, то пропорція істинна.
Приклади
1) 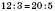 – істинна пропорція, оскільки
– істинна пропорція, оскільки 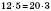 .
.
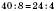 – неістинна пропорція; дійсно,
– неістинна пропорція; дійсно, 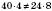 .
.Якщо в істинній пропорції поміняти місцями середні або крайні члени, то отримаємо нові істинні пропорції:
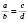 ;
; 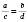 ;
; 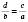 ;
; 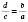 .
.Якщо три члени істинної пропорції відомі, то невідомий член можна знайти, скориставшись основною властивістю пропорції. Наприклад:
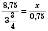 ;
;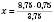 ;
;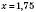 .
.Related posts:
- Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...
- Пропорція, члени пропорції. Основні властивості пропорції Урок № 4 0 Тема. Пропорція, члени пропорції. Основні властивості пропорції Мета: сформувати уявлення учнів про зміст понять пропорція, члени пропорції, основна властивість пропорції та виробити вміння застосовувати ці поняття під час розв’язування типових завдань, що передбачають їх застосування. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань @ […]...
- Розв’язування рівнянь на основі властивостей пропорції Урок № 4 1 Тема. Розв’язування рівнянь на основі властивостей пропорції Мета: закріпити знання, набуті на попередньому уроці, виробити вміння і відпрацювати стійки навички розв’язування рівнянь на основі властивості пропорції. Тип уроку: формування вмінь і навичок. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Закінчіть речення: “Рівністю двох відношень називають…” [Якщо […]...
- Відношення. Пропорції Урок № 5 0 Тема. Відношення. Пропорції Мета: перевірити рівень засвоєних знань і набутих умінь з теми. Тип уроку: перевірка і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент II. Умови тематичної контрольної роботи Варіант 1 1. Чи істинна пропорція 1 : 4 = 1 : 2? 2. Знайдіть невідомий член пропорції: 1,6 […]...
- Пропорція. Основна властивість пропорції Розділ 3 Відношення і пропорції §21. Пропорція. Основна властивість пропорції Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність Рівність двох відношень називають пропорцією. Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так: Ці […]...
- Відношення. Основна властивість відношення Розділ 3 Відношення і пропорції У цьому розділі ви: – згадаєте про коло, круг та відсотки; j ознайомитеся з поняттями відношення та пропорції, масштабу, випадкової події; – дізнаєтеся про стовпчасті та кругові діаграми, циліндр, конус, кулю; – навчитеся розв’язувати рівняння на основі властивості пропорції, знаходити ймовірність випадкової події, здійснювати відсоткові розрахунки, розв’язувати задачі на пряму […]...
- ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ У розділі дізнаєтесь: Ü про відношення та його властивості; Ü що таке пропорція; Ü які є пропорційні залежності величин; Ü як поділити число в даному відношенні; Ü що таке масштаб; Ü про коло, круг, круговий сектор та просторові фігури обертання; Ü які є види діаграм та як будувати діаграми; Ü […]...
- Відношення. Властивості відношення Урок № 39 Тема. Відношення. Властивості відношення Мета: узагальнити знання учнів про зміст дії ділення чисел; сформувати уяву про поняття відношення двох чисел, його змісту, властивості, а також сформувати уяву про взаємно обернені відношення. Тип уроку: засвоєння нових знань. Хід уроку І. Актуалізація опорних знань Усні вправи 1. Обчисліть значення виразів: 2. Скоротіть дріб: ; […]...
- Відсоткове відношення двох чисел. Зміна величини у відсотках Розділ 3 Відношення і пропорції §27. Відсоткове відношення двох чисел. Зміна величини у відсотках Ми знаємо два види задач на відсотки: знаходження відсотків від числа та знаходження числа за його відсотками. Розглянемо ще задачі, у яких треба знайти, скільки відсотків складає одне число від іншого, тобто відсоткове відношення двох чисел. Ми вміємо знаходити відношення двох […]...
- Пропорції народного господарства Пропорції народного господарства (від лат. proportio – розмірність) – співвідношення між сферами і галузями народного господарства, між стадіями суспільного відтворення, між різними регіонами країни, внутрігалузеві та міжвиробничі пропорції тощо. Пропорції між сферами (загальноекономічні) – це співвідношення між виробничою і невиробничою сферами, між промисловістю і сільським господарством, між І і II підрозділами тощо. Міжгалузеві пропорції – […]...
- ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ §13. ПРОПОРЦІЯ ТА її ВЛАСТИВОСТІ Ви знаете, що два вирази, які мають рівні значення, можна прирівняти. Наприклад, можна прирівняти відношення 1,2 : 0,3 і 16 : 4, оскільки їх значення дорівнюють 4. Отже, можна записати рівність: Такі рівності мають спеціальну назву – пропорція. Пропорцією називається рівність двох відношень. Зверніть увагу: […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Основні пропорції світової економіки Основні пропорції світової економіки – співвідношення між окремими підрозділами, підсистемами та елементами світового господарства, які характеризують стан та закономірності його розвитку здебільшого у межах технологічного способу виробництва за певний період. О. п. с. е.: між основними групами країн (розвиненими, тими, що розвиваються, і країн з перехідною економікою); співвідношення між попитом і пропозицією на світовому ринку; […]...
- Властивості степеня (продовження). Степінь добутку й відношення Урок № 24 Тема. Властивості степеня (продовження). Степінь добутку й відношення Мета: домогтися свідомого розуміння властивості степеня добутку й відношення; виробити вміння застосовувати ці властивості для перетворень виразів і обчислення значень числових виразів. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ Як і на попередніх двох уроках, перевірку домашнього […]...
- Правила знаходження первісних – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила знаходження первісних Правило 1. Якщо функції у = f(x) і у = g(x) мають на числовому проміжку X первісні, відповідно у = F(x) й у = G(x), то і сума функцій у = f(x) + g(x) має на проміжку X первісну у= =F(x) + G(x). (Первісна суми дорівнює […]...
- Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила диференціювання Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних: Правило 2. Якщо функція у = f(x) має похідну в точці х, то і […]...
- ЗАДАЧІ, ЯКІ ДВІЧІ МІСТЯТЬ ВІДНОШЕННЯ “НА… БІЛЬШЕ” (“менше”). ПОНЯТТЯ “ДОВЖИНА” І “ШИРИНА” ПРЯМОКУТНИКА. САМОСТІЙНА РОБОТА ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ВИРАЗИ З ДУЖКАМИ Урок 31. ЗАДАЧІ, ЯКІ ДВІЧІ МІСТЯТЬ ВІДНОШЕННЯ “НА… БІЛЬШЕ” (“менше”). ПОНЯТТЯ “ДОВЖИНА” І “ШИРИНА” ПРЯМОКУТНИКА. САМОСТІЙНА РОБОТА Мета: ознайомити учнів із задачами, які двічі містять відношення “на… більше” (“менше”), з поняттями “довжина” і “ширина” прямокутника; удосконалювати обчислювальні навички; розвивати кмітливість, […]...
- Відношення площ подібних трикутників Урок № 50 Тема. Відношення площ подібних трикутників Мета: домогтися засвоєння учнями змісту та ідеї доведення теореми про відношення площ подібних трикутників. Сформувати вміння відтворювати зміст теореми та застосовувати її під час розв’язування задач. Тип уроку: засвоєння вмінь та навичок. Наочність та обладнання: конспект “Відношення площ подібних трикутників”. Хід уроку І. Організаційний етап II. Перевірка […]...
- Пропорції економічні Пропорції економічні – визначені за певними критеріями кількісно-якісні співвідношення між окремими підсистемами, елементами та компонентами народного господарства. За матеріально-речовою ознакою розрізняють передусім трудові (забезпеченість країни трудовими ресурсами, працівників – робочими місцями, співвідношення між підготовленою кваліфікованою і не кваліфікованою робочою силою та ін.), речові (характеризують на мікро – та макрорів – ні співвідношення певних видів продукції […]...
- Відсоткове відношення двох чисел Урок № 4 5 Тема. Відсоткове відношення двох чисел Мета: сформувати уявлення про зміст поняття відсоткове відношення двох чисел та виробити вміння знаходити відсоткове відношення двох чисел та розв’язувати задачі, що передбачають цю дію. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Актуалізація опорних знань Усні вправи 1. Обчисліть: 2. Знайдіть відношення чисел: 15до5; […]...
- Відсоткове відношення чисел Урок № 4 6 Тема. Відсоткове відношення чисел Мета: спираючись на вміння учнів знаходити відсоткове відношення чисел, навчити знаходити вміст величини у відсотках і розв’язувати задачі, що передбачають ці дії. Тип уроку: засвоєння знань, вмінь та навичок. Хід уроку І. Перевірка домашнього завдання Вибірково перевіряємо зошити (у “слабких” учнів). Правильні відповіді записуємо за дошкою, і […]...
- Одиниці вимірювання маси. Задачі, які розв’язуються способом відношення (№№ 327-337) Тема. Одиниці вимірювання маси. Задачі, які розв’язуються способом відношення (№№ 327-337). Мета. Систематизувати знання учнів про одиниці вимірювання маси; формувати уміння замінювати одиниці вимірювання маси іншими; вправляти у розв’язуванні задач способом відношення. Обладнання. Таблиця “Одиниці вимірювання маси”, “Народні міри маси”; “Картки для поточного контролю знань”. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Похідні елементарних функцій – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Похідні елементарних функцій Y = f(x) Y = f'(x) Y = f(x) Y = f'(x) Y = c (c = const) Y’ = 0 У = ax + b Y’ = a Y = xn Y’ = nxx-1 Y = x Y’ = 1 Y = 1/x Y’ = […]...
- Формули скороченого множення Математика – Алгебра Многочлен Формули скороченого множення – Формула різниці квадратів. Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів. – Формула квадрата суми. Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу. – Формула квадрата різниці. Квадрат різниці двох виразів дорівнює квадрату […]...
- Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
- Міжгалузеві та внутрігалузеві пропорції Міжгалузеві та внутрігалузеві пропорції – кількісно-якісні співвідношення матеріально-речових та особистісних факторів виробництва між галузями або окремими виробництвами чи підгалузями. Кількість таких пропорцій залежить від ступеня розвитку суспільного поділу праці у загальній та особливій формах. Якісний аспект М. та в. п. зумовлюється передусім рівнем розвитку продуктивних сил. У розвинених країнах світу якісні співвідношення виражаються у незначній […]...
- КОРЕЛЯЦІЙНЕ ВІДНОШЕННЯ Соціологія короткий енциклопедичний словник КОРЕЛЯЦІЙНЕ ВІДНОШЕННЯ – міра кореляційного зв’язку між двома кількісними змінними. Інша назва – коефіцієнт eta. На відміну від коефіцієнта кореляції Пірсона г коефіцієнт eta не потребує припущення про лінійність зв’язку. Коефіцієнт eta є несиметричним показником, отже, для двох змінних X та Y можна (якщо це має сенс з т. з. задачі, […]...
- Об’ємні відношення газів у хімічних реакціях. Закон Авогадро Хімія Загальна хімія Основні поняття, закони й теорії хімії Об’ємні відношення газів у хімічних реакціях. Закон Авогадро Закон об’ємних відношень Гей-Люссака Гази реагують між собою у певних об’ємних відношеннях. У 1808 р. Ж. Л. Гей-Люссак установив таку закономірність: Об’єми газів, що вступають у реакцію, відносяться один до одного і до газоподібних продуктів реакції як невеликі […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...